
|
Читайте также: |
Осы уақытқа дейін қарастырып келген ықтималдықтар интуитивті түрде теориялық болжамдарға сүйеніп, тәжірибе жүргізбей-ақ, комплекс шарт жөніндегі білім (түсінік) негізінде анықталып келді. Тәжірибеге дейінгі Н1, Н2,...,Нп гипотезалар (оқиғалар) ықтималдығы сәйкес түрде р(Н1), р(Н2),...,р(Нп) болатынды.
Тәжірибе жүргізілді делік, соның нәтижесінде В оқиғасының пайда болғаны анықталды, енді осы В оқиғасының пайда болуына байланысты Н1, Н2,...,Нп гипотезаларының ықтималдығын қайта қарауға тура келеді. Яғни  ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.
ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.
Тәуелді оқиғалар В мен  үшін
үшін
 (1)
(1)
Бұдан
 (2)
(2)
шығады. Бұл формулаға толық ықтималдық формуласынан  мәнін қойсақ, онда
мәнін қойсақ, онда
 (3)
(3)
шығады. Осы (3) формуланы Байес формуласы деп айтады.
--Ереже бойынша, оқытылатын таңдаудағы элементтерді кәдімгі жағдайларда алуға болады. Қандай да бір бейненің келіп түсуі кездейсоқ оқиға болып табылады және оның пайда болу ықтималдылығын орнату тығыздығы функциясы көмегімен сипаттауға болады. Бұл функция тану жүйесі жұмыс істейтін нақты ортамен анықталады. Таңдаудағы элементтерді біле отырып, осы ортаның ықтималдылық ортасын қайта тұрғызуға болады. Мұндай сипаттауларға келесілер жатады:
·  белгілер векторы (бейнелер) ықтималдылықтарының пайда болуын орнату тығыздық функциясы;
белгілер векторы (бейнелер) ықтималдылықтарының пайда болуын орнату тығыздық функциясы;
·  класс ішінде белгілердің ықтималдылықтарын орнатуының шартты тығыздық функциясы
класс ішінде белгілердің ықтималдылықтарын орнатуының шартты тығыздық функциясы  ;
;
· 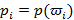 кластардың пайда болу ықтималдылығы;
кластардың пайда болу ықтималдылығы;
· қандай да бір  бейненің пайда болуында кластардың пайда болу ықтималдылығы.
бейненің пайда болуында кластардың пайда болу ықтималдылығы.
Мысалы. Ағаш өңдейтін фабрикада ағашты тану жүйесін қарастырайық. Фабрикаға ағаштың түрлі түрлерінен тақтайлар түсті деп алайық. Тану жүйесі қандай да бір сипаттауларға байланысты келіп түскен тақтайларды түрлеріне қарай танып, сұрыптау қажет. Мұндай сипаттауларға келесілер:  -ағаш түсі,
-ағаш түсі,  -ағаш қаттылығы,
-ағаш қаттылығы,  -ағаштың тығыздығы таңдалсын. Сонда
-ағаштың тығыздығы таңдалсын. Сонда  ) ықтымалдылығын берілген ағаштың
) ықтымалдылығын берілген ағаштың  сипаттамасымен
сипаттамасымен  ағаш түріне жататындығын қарастыра аламыз.
ағаш түріне жататындығын қарастыра аламыз.
Ортаның көрсетілген ықтималдылық сипаттамалары төмендегі формулармен байланысты:
· толық ықтималдылықты формула 
· Байес формуласы: 
(8.1)-формуласында  кластары толық оқиғасы (болжамдар болып табылады) бар топтарды құрады, яғни
кластары толық оқиғасы (болжамдар болып табылады) бар топтарды құрады, яғни  үшін
үшін
 .
.
Мысалы. Екі қиылыспайтын  және
және  кластары болсын және
кластары болсын және  бейнелерінің шартты орнату тығыздығы берілген
бейнелерінің шартты орнату тығыздығы берілген  класында
класында
 тең.
тең.  функцияның
функцияның  және
және  параметрлерін кездейсоқ
параметрлерін кездейсоқ  таңдауларын максималды шынайылық әдісі бойынша келесі түрде бағалауға болады:
таңдауларын максималды шынайылық әдісі бойынша келесі түрде бағалауға болады:

 (8.2)
(8.2)
Қандай да бір кластың пайда болу ықтималдылығын келесі формула бойынша бағалаймыз:  , мұндағы
, мұндағы 
 класына жататын элементтер саны. (8.1) және (8.2) формулалар бойынша ортаның сипаттамасын тауып, бағалауға болады.
класына жататын элементтер саны. (8.1) және (8.2) формулалар бойынша ортаның сипаттамасын тауып, бағалауға болады.
Есептің қойылуы.  векторының
векторының  немесе
немесе  кластарының біреуіне классификациялау кезінде минималды қателікпен қай класқа жататындығын анықтау керек.
кластарының біреуіне классификациялау кезінде минималды қателікпен қай класқа жататындығын анықтау керек.  белгілер кеңістігін екі қиылыспайтын
белгілер кеңістігін екі қиылыспайтын 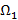 және
және  облыстарға бөлейік, егер
облыстарға бөлейік, егер 
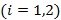 болса, онда
болса, онда  жатады. Онда дұрыс емес классификациялаудың қателік жіберу ықтималдылығы келесі формула бойынша есептелінеді:
жатады. Онда дұрыс емес классификациялаудың қателік жіберу ықтималдылығы келесі формула бойынша есептелінеді:
 (8.3)
(8.3)
(8.3)-формуласындағы бірінші қосылғыш  векторының
векторының  класына жатады, шынында ол
класына жатады, шынында ол  класына жататын болса (
класына жататын болса ( ықтималдылығы екінші ретті ықтималдылық) және екінші қосылғыш –
ықтималдылығы екінші ретті ықтималдылық) және екінші қосылғыш – 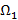 ықтималдылығы бірінші ретті қателік болып саналады. (8.3)-өлшемі дұрыс емес классификациялаудың орташа қателігі болып табылады.
ықтималдылығы бірінші ретті қателік болып саналады. (8.3)-өлшемі дұрыс емес классификациялаудың орташа қателігі болып табылады.
Бұдан, ең дұрыс классификаторды тұрғызу -  дұрыс емес классификациясының орташа қателігін минимизациялайтын
дұрыс емес классификациясының орташа қателігін минимизациялайтын  кеңістігін қиылыспайтын
кеңістігін қиылыспайтын 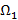 және
және  облыстарға бөлумен эквивалентті. Байестік классификаторға сәйкес, егер
облыстарға бөлумен эквивалентті. Байестік классификаторға сәйкес, егер  болса, онда
болса, онда 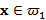 жатады және егер
жатады және егер  жатады.
жатады.
Мысалы. Белгілерді  кластар ішінде орнатуының шартты тығыздығы
кластар ішінде орнатуының шартты тығыздығы  болғанда,
болғанда,  тең. Онда байестік классификатор ережесіне сәйкес егер
тең. Онда байестік классификатор ережесіне сәйкес егер  болса, онда
болса, онда 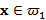 жатады және
жатады және

немесе
егер  болса, онда
болса, онда
 .
.
HSB түстік моделі адамның түс қабылдау ерекшеліктерін жан-жақты есепке
ала отырып жасалған. Ол Манселдің түс шеңбері негізінде тұрғызылған. Түс үш
компонентпен: ӛңмен, қанықтылықпен, жарықтықпен сипатталады. Түстің
мәнін шеңбердің центрінен шыққан вектор түрінде таңдайды. Центрдегі нүкте
ақ түске, ал шеңбердің периметріндегі нүктелер – таза спектрлі түстерге сәйкес
келеді. Вектор бағыты градуспен беріліп, түстің реңін сипаттайды. Вектордың
ұзындығы түстің қанықтылығын сипаттайды. Ахроматикалық деп аталатын
ӛсте жарықтығы беріледі, бұл жағдайда нӛлдік нүкте қара түске сәйкес келеді.
HSB моделінің түс қамтуы нақты түстердің бізге белгілі барлық мәндерін
қабылдайды. HSB моделін компьютерде бейне құруда суретшінің жұмыс
әдістерін имитациялау мен құралы ретінде қолдану қабылданған. Қаламсап,
сауыт, кисттерді имитациялайтын арнайы программалар бар. Олар арқылы әр
түрлі тұстармен және бояулармен жұмыс имитациясы қамтамасыз етіледі.
Бейне құрғаннан кейін жарияланым түріне қарай оны ӛзге түстік модельге
түрлендіру ұсынылады.

Билет
Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.
Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:
· символдарды тануда (баспа және жазба мәтіндерінде, банк чектерінде және т.б.);
· әртүрлі жиілік диапазонда (оптикалық, инфрақызыл, дыбыстық, радиожиілікті) алынған бейнелер мен сахнаны талдауда;
· медициналық диагностикада;
· қауіпсіздік жүйелерінде;
· дыбыстарды тануда;
· деректер қорында және білімде (сонымен қатар, Интернет-ресурстарында) іздеу және классификациялауда, кластеризациялауда қолданылады.
Бейнелерді тану теориясының негізгі есептері. Сандарды, әріптерді және т.б. символдарды тануды іске асыратын техникалық жүйе мысалында бейнелерді тану теориясының негізгі есептерін қарастырайық. Мұндай жүйе 60-жылдары АҚШ-да жасалған және ұзақ уақыт бойы конвертті символдарды тану үшін қолданылған.
Мысалы, тану жүйесінің кірісіне қағаз лентада жазылған қандай да бір х символы келіп түссін және осы символды тану керек болсын. Тану керек объектілерді бейне («pattern») деп атайды. Солдан оңға қарай жылжитын есептеуші басы бар техникалық жүйе  уақытына тәуелді боялған бет ауданының өзгерісін
уақытына тәуелді боялған бет ауданының өзгерісін  жылдамдығы өлшейді (1.1-сурет).
жылдамдығы өлшейді (1.1-сурет).  символ-бейнесінің
символ-бейнесінің  функциясы оның бейнеленуі болып табылады. Сигналды уақыттың дискретті нүктелерінде өлшесек, х символын х векторы түрінде аламыз.
функциясы оның бейнеленуі болып табылады. Сигналды уақыттың дискретті нүктелерінде өлшесек, х символын х векторы түрінде аламыз.  функциясын функциялар кеңістігінде элемент-вектор деп есептей аламыз. Бір түрден екінші түрге ауысу, ереже бойынша, бейне туралы ақпараттар санын азайтады.
функциясын функциялар кеңістігінде элемент-вектор деп есептей аламыз. Бір түрден екінші түрге ауысу, ереже бойынша, бейне туралы ақпараттар санын азайтады.

Сурет 1.1
Кіріс х символ-бейнесі  кластар жиынының қандай да бір класына жатуы мүмкін - әрбір класс қандай да бір символға (әріпке, санға және т.б.) сәйкес келеді. Кластарды бір-бірімен қиылыспайды деп аламыз.
кластар жиынының қандай да бір класына жатуы мүмкін - әрбір класс қандай да бір символға (әріпке, санға және т.б.) сәйкес келеді. Кластарды бір-бірімен қиылыспайды деп аламыз.




| Оқыту |
| Белгілерді таңдау |
| Классификатор |
| Бейнені векторлық форма түрлендіру |
Сурет 1.2 Бейнелерді тану жүйесінің жалпы сызбасы
Бейнелерді тану есебі х бейнесінің 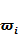 кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады. Егер бейне метрикалық кеңістіктің элемент-векторы болса, бейнені класқа жатқызуды, мысалы, вектор мен класс арасындағы қашықтықты есептеу көмегімен іске асыра аламыз. Классификатор шығысында кіріс бейнесінің қай класқа (класс номерін) жататындығын немесе ешқандай класқа жатпайтындығын анықтауымыз қажет.
кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады. Егер бейне метрикалық кеңістіктің элемент-векторы болса, бейнені класқа жатқызуды, мысалы, вектор мен класс арасындағы қашықтықты есептеу көмегімен іске асыра аламыз. Классификатор шығысында кіріс бейнесінің қай класқа (класс номерін) жататындығын немесе ешқандай класқа жатпайтындығын анықтауымыз қажет.
Бейненің векторлық формаға түрлендіру бөлімімен классификатор арасында кішкене санды таңдау бөлімі (мысалы,  аналогты сигналының х векторына түрленуі) болуы мүмкін. Мұндай бөлімнің болуы вектор өлшемін азайтып, тану жүйесінің жылдамдығын арттырады.
аналогты сигналының х векторына түрленуі) болуы мүмкін. Мұндай бөлімнің болуы вектор өлшемін азайтып, тану жүйесінің жылдамдығын арттырады.
Жалпы, тану жүйесінде оқыту бөлімі болуы мүмкін. Бұл бөлім оқытылатын бейнелерді таңдау кезінде классификация ережесін қалыптастыруға мүмкіндік береді. Сонымен қатар, оқытылатын бейнелер бойынша ақпараттық белгілерді таңдау ережесі қалыптасады.
Бейнелер сипатының типтері. Белгілердің сипаты негізгі үш типімен ерекшеленеді:
5. Физикалық түрде сипатталуы, мысалы, әртүрлі датчиктерден алынған көрсеткіштер. Физикалық түрде сипатталуы детерминирленген және ықтималдылықты болуы мүмкін және бұл сипатталуды векторлар көмегімен сипаттап, векторлық кеңістіктің элементтері ретінде қарастыруға оңай болады.
6. Сапалы түрде сипатталуы. Сапалы түрде сипатталуда “ашық”, “жоғары”, “төмен” және т.б. түсініктер мысал бола алады. Мұндай сипаттамалар бұлдыр жиындар теориясы әдістерінің лингвистикалық айнымалылар көмегімен сипатталуы мүмкін.
7. Құрылымдық түрде сипатталуы. Бұл сипатталу күрделі объектілер (1.3-сурет) немесе сахналардың бейнелерін сипаттау үшін қолданылады. Құрылымдық сипаттауда формальды тіл - графтар теориясы (1.4-сурет) болып табылады.
8. Логикалық түрде сипатталуы – бұл ақиқат немесе жалған болатын сөйлем болып табылады.

Сурет 1.3 Сурет 1.4
2.Метрика Минковского
Обьектілер арасындағы қашықтықты өлшеу оларда белгіленген нүктелердің жақынына запрос жіберіліп іздеу жүргізіледі. Ал қашықтықтықты анықтау үшін кеңістіктегі обьектілерге анализ жургізіледі. Анализ бойынша нүктелерді ортақ қасиеті, олардың бір нүктеге ойысуы, олардың тобы, шоғыры бойынша бірнеше жазықтыққа бөлу керек. Өлшенетін қашықтық шамасына нөлден кіші болмау және барып қайтар жол тең секілді шарттар қойылады. Қашықтықтың екінші бір термині ол метрика деп аталады. Сондай метрикалардың бірі Минковский метрикасы.

Иллюстрация парадоксаблизнецов на диаграммеМинковского.
Простра́нство Минко́вского ― четырёхмерное псевдоевклидово пространство сигнатуры  ,предложенное Германом Минковским в 1908 году в качестве геометрической интерпретации пространства-времени специальной теории относительности.
,предложенное Германом Минковским в 1908 году в качестве геометрической интерпретации пространства-времени специальной теории относительности.
Каждому событию соответствует точка пространства Минковского, в лоренцевых (или галилеевых)координатах, три координаты которой представляют собой декартовы координаты трёхмерного евклидовапространства, а четвёртая ― координату ct, где c ― скорость света, t ― время события. Связь между пространственными расстояниями и промежутками времени, разделяющими события, характеризуется квадратом интервала:
s 2 = c 2(t 1 − t 0)2 − (x 1 − x 0)2 − (y 1 − y 0)2 − (z 1 − z 0)2.
(Нередко в качестве квадрата интервала берется противоположная величина, выбор знака — вопроспроизвольного соглашения. Так, первоначально сам Минковский предложил именно противоположный знакдля квадрата интервала).
Интервал в пространстве Минковского играет роль, аналогичную роли расстояния в геометрии евклидовыхпространств. Он инвариантен при замене одной инерциальной системы отсчета на другую, так же, какрасстояние инвариантно при поворотах, отражениях и сдвигах начала координат в евклидовомпространстве. Роль, аналогичную роли вращений координат в случае евклидова пространства, играют дляпространства Минковского преобразования Лоренца.
Интервал аналогичен квадрату расстояния в евклидовом пространстве. В отличие от последнего интервалне положителен, также между различными событиями интервал может быть равен нулю.
3.СМYK түстік моделі
CMYK түстік моделі субстрактивті болып табылады және оны
жарияланымды баспаға дайындауда қолданады. СМҮK-дің түстік
компоненттеріне ақ түстен бөлініп алынған негізгі түстер қызмет етеді.
көгілдір (cyan) = ақ – қызыл = жасыл + көк
күлгін (magenta) =ақ – жасыл = қызыл + көк
сары(yellow) = ақ – көк = қызыл + жасыл
Мұндай әдіс түпнұсқадағы баспадан шағылған сәуленің физикалық
табиғатына сай келеді. Көгілдір, күлгін және сары түстерді толықтырушы деп
аталады, себебі олар негізгі түстерді ақ түске дейін толықтырады. Бұдан СМҮK
түстік моделінің басты проблемасы – толыктырушы түстерді іс жүзінде бірінің
үстінде бірін қолдану таза қара түсті алуға мүмкіндік бермейтіндігі келіп
шығады. Сондықтан да түстік модельге таза қара түс компоненті қосылған.
СМҮК түстік моделінің аббревиатурасындағы төртінші әріп (Cyan, Magenta,
Yellow, black) осылайша пайда болған. Түрлі-түсті компоненттерлік бейнені
полиграфиялық құралда басу үшін СМҮК түстік моделінің компоненттерімен
сәйкес келетін құрамдас бөліктерге бөлу қажет. Бұл процесті түс бөлу деп
атайды. Нәтижесінде түпнұсқада компоненттің түсінен тұратын төрт жеке
бейне алынады.
Билет
Бейнелер арасындағы қашықтықты өлшейтін өлшем кеңістігін анықтағаннан кейін, бейне мен класс арасындағы қашықтықты есептеу есебін шешу керек. Бейнелерді тануды оқыту жағдайында қандай да бір элементтердің оқытылатын кластарға жататындығын ғана білеміз. Бұл есепті шешудің бірнеше әдістері бар.
Бірінші әдіс - бейне мен класс центрі арасындағы қашықтықты анықтау. Бұл әдісті бір эталонды бейне – класс центрімен сипатталған кезде және дұрыс емес классификациялауда қателік құны көп емес жағдайларда қолдану тиімді. Бұл әдісті белгілер кеңістігіндегі бір класта орналасқан бейне-векторлардың бір-біріне өте жақын орналасуы қажет. Осы жағдайда қашықтықты анықтау келесі қадамдардан тұрады:
a)  класының
класының  центрлері анықталады:
центрлері анықталады:

яғни класс центрі дегеніміз- класс нүктелерінің арифметикалық ортасы болып табылады. Егер тануды оқытумен қарастыратын болсақ, онда келтірілген жоғарыдағы формулада оқытылатын таңдаудағы элементтер болып сол класқа нақты жататын элементтердің қосындысы қарастырылады.
b)  бейнесі мен
бейнесі мен  класы арасындағы қашықтық бейне мен класс центрі
класы арасындағы қашықтық бейне мен класс центрі  арасындағы қашықтық ретінде қарастырылады:
арасындағы қашықтық ретінде қарастырылады: 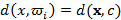 . Мысалы,
. Мысалы,  және
және 
Бірнеше дербес жағдайларды қарастырайық.
1.  және
және  екі кластар бойынша классификациялау. Оқытылатын
екі кластар бойынша классификациялау. Оқытылатын  таңдауы белгілі болсын. Оның қандай-да элементтері
таңдауы белгілі болсын. Оның қандай-да элементтері  класына, ал қандай-да элементтері
класына, ал қандай-да элементтері  класына жатсын. Егер
класына жатсын. Егер  болса, онда
болса, онда  деп есептейміз. Сондықтан, шешуші функция ретінде
деп есептейміз. Сондықтан, шешуші функция ретінде  немесе
немесе  алуға болады, яғни
алуға болады, яғни


Осылайша, шешуші функция сызықты функция болады, ал  теңдеуімен берілген бөлуші бет класс центрлерін біріктіретін, кесіндіге перпендекуляр түсетін түзу болады. (1-суретте көрсетілген.)
теңдеуімен берілген бөлуші бет класс центрлерін біріктіретін, кесіндіге перпендекуляр түсетін түзу болады. (1-суретте көрсетілген.)

Сурет 3.1 Екі класс арасындағы арақашықтық
2. Үш класс бойынша классификациялау. Класс шекараларының қашықтығын өлшеу – бұл класс центрлері арасындағы перпендикулярлар ортасы болады (3.2-сурет) және перпендикулярлардың қиылысу нүктесі – класс центрлерінің сыртынан жүргізілген шеңбер центрлері болып табылады.
Дата добавления: 2015-08-26; просмотров: 674 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Минковский метрикасы | | | Байес формуласы 2 страница |