|
Читайте также: |
Векторлар арасындағы өлшенетін қашықтықтың әртүрлі өлшемі, белгілердің басымдылықтары болуы мүмкін. Сондықтан салмақтық өлшемдер қарастырылады. Мысалы, Минковский салмақтық өлшемі келесі түрде болады:
,
мұндағы оң салмақ векторы 
белгілердің басымдылықтары мен шамасы жөнінде ақпаратпен анықталады. Егер мұндай ақпарат векторды анықтау үшін аз болса, онда өлшенетін шамаларды нормалайтын, мысалы Канберра өлшемін қолданамыз:
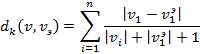
Бейнелер арасындағы қашықтықты өлшейтін өлшем кеңістігін анықтағаннан кейін, бейне мен класс арасындағы қашықтықты есептеу есебін шешу керек. Бейнелерді тануды оқыту жағдайында қандай да бір элементтердің оқытылатын кластарға жататындығын ғана білеміз. Бұл есепті шешудің бірнеше әдістері бар.
Бірінші әдіс - бейне мен класс центрі арасындағы қашықтықты анықтау. Бұл әдісті бір эталонды бейне – класс центрімен сипатталған кезде және дұрыс емес классификациялауда қателік құны көп емес жағдайларда қолдану тиімді. Бұл әдісті белгілер кеңістігіндегі бір класта орналасқан бейне-векторлардың бір-біріне өте жақын орналасуы қажет. Осы жағдайда қашықтықты анықтау келесі қадамдардан тұрады:
a) 
класының 
центрлері анықталады:
яғни класс центрі дегеніміз- класс нүктелерінің арифметикалық ортасы болып табылады. Егер тануды оқытумен қарастыратын болсақ, онда келтірілген жоғарыдағы формулада оқытылатын таңдаудағы элементтер болып сол класқа нақты жататын элементтердің қосындысы қарастырылады.
b) 
бейнесі мен класы арасындағы қашықтық бейне мен класс центрі 
арасындағы қашықтық ретінде қарастырылады: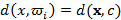 
. Мысалы, 
және 
Бірнеше дербес жағдайларды қарастырайық.
1. 
және 
екі кластар бойынша классификациялау. Оқытылатын 
таңдауы белгілі болсын. Оның қандай-да элементтері 
класына, ал қандай-да элементтері 
класына жатсын. Егер 
болса, онда 
деп есептейміз. Сондықтан, шешуші функция ретінде 
немесе 
алуға болады, яғни
Осылайша, шешуші функция сызықты функция болады, ал 
теңдеуімен берілген бөлуші бет класс центрлерін біріктіретін, кесіндіге перпендекуляр түсетін түзу болады. (1-суретте көрсетілген.)
Сурет 3.1 Екі класс арасындағы арақашықтық
2. Үш класс бойынша классификациялау. Класс шекараларының қашықтығын өлшеу – бұл класс центрлері арасындағы перпендикулярлар ортасы болады (3.2-сурет) және перпендикулярлардың қиылысу нүктесі – класс центрлерінің сыртынан жүргізілген шеңбер центрлері болып табылады.
Сурет 3.2 Үш класс арасындағы қашықтық
№9 ЕМТИХАН БИЛЕТІ
Тану сызбасын талдай отырып, келесі бейнелерді тану теориясының негізгі есептерін ерекшелеуге болады:
6. Бейнелердің математикалық сипатталуы. Бейнелерді математикалық сипаттаудың ең тиімді әдісінің бірі - бейнелерді векторлық сипаттау болып табылады. Бұл жағдайда әрбір х бейнесіне сәйкесінше Х векторлық кеңістігінің элементі, яғни осы бейненің 
белгілерінің қандай да бір x= 
векторы сәйкес келеді. Мұндай векторлық кеңістік белгілер кеңістігі деп аталады. Ереже бойынша, бұл кеңістік шекті өлшемді және метрикалық болып табылады. Егер бұл кеңістіктің белгілері нақты шамалар болса, онда мұндай кеңістік 
метрикалық кеңістігіне изоморфты, ал n – белгілер кеңістігінің өлшемі болып есептеледі.
Кейбір тану есептерінде (мысалы, суреттерді тануда) белгілер векторының әртүрлі ұзындығы болуы мүмкін.
7. Берілген бейнені сипаттайтын ақпараттық белгілерді таңдау. Бұл бейнелерді тану теориясында негізгі және маңызды есептердің бірі – берілген тану есебінде бейнелерді нақтырақ сипаттайтын, белгілердің минималды санын анықтау болып табылады.
Белгілерді тану үшін толық таңдау жиынын белгілер алфавиті, ал тану есебінің берілген класы үшін жеткілікті ең аз белгілер жиынын белгілер сөздігі деп атайды. Белгілер сөздігі белгілер алфавитінің ішкі жиыны болмауы да мүмкін, яғни ол белгілер алфавиті элементінің кейбір функцияларынан тұруы да мүмкін. Жалпы жағдайда, жүйе белгілер сөздігін өзі анықтау қажет.
8. Танылатын бейнелердің кластарын сипаттау. Бұл есеп кластардың шекараларын анықтайды. Кластар шекаралары тану жүйесінің жасалу кезеңінде нақты берілуі мүмкін немесе жүйе өзінің жұмысы барысында өзі табуы керек.
9. Тиімді шешуші әдістерді табу, яғни бейненің белгілер векторын қандай да бір класқа жатқызу керек.
10. Бейнелерді классификациялаудың нақтылығын бағалау. Шешім қабылдайтын адам немесе техника бейнені қандай-да бір класқа жатқызу арқылы классификацияның қателігіне байланысты қателік шамасын бағалай алу қажет.
2. Нейрондық желісі және Хэмминг алгоритмі.
Бұл желіде биполярлы векторлар үшін Хеммингтің қашықтық қасиеті қолданылады. Егер екі биполярлы векторлар 
және 
, 
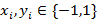болса, онда 
арасындағы Хемминг қашықтығы 
тең, мұндағы 
-осы векторлардың түрлі компонент саны. Егер 
– x және y векторларының сәйкес келетін компоненттер саны, ал 
-осы векторлардың өлшемі болса, онда
тең. Онда екі биполярлы векторлар арасындағы жақындық өлшемі 
тең. Егер 
эталонды векторлар бар болса, онда кіріс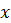 
векторы мен 
эталонды вектор арасындағы жақындық өлшемі келесі формуламен анықталады:
Осылайша, 
-шы нейронның синапсы 
векторы болса, мұндағы 
, онда нейрон кірісіне келіп түсетін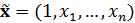 
векторы шығысында берілген вектор мен k -шы вектор эталон арасындағы жақындық өлшемін аламыз.
Хэмминг нейрондық желісі екі қабаттан тұрады. Бірінші қабатта m нейрондар (эталондар санына байланысты), олардың әрқайсысына кіріс 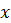векторының барлық компоненттері келіп түседі. Осы қабаттың әрбір -шы нейроны x векторының эталонды векторы арасындағы 
жақындық өлшемін есептейді. Екінші қабатта (Maxnet желісі деп аталатын) жақындық өлшем векторы 
векторына түрлендіріледі және ол жақта бір нольдік емес компонент болады. Осы компоненттің номері жақын орналасқан эталон номеріне тең болуы керек. Maxnet желісі толық байланысқан және m нейроннан тұратын бір қабатты болып есептеледі. Әрбір нейронның шығыс сигналдары барлық нейрон желісінің кірісіне келіп түседі. Желі итерационды режимде, шығыс нейрондары тұрақталмағанша жұмыс жасайды. Хэмминг желісі келесі 7.1-суретте бейнеленген.
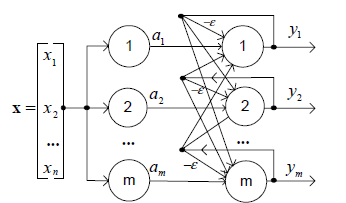
Сурет 7.1 Хемминг желісінің құрылымы
Хэмминг алгоритмі келесі қадамдардан тұрады:
1. Бірінші қабат кірісіне сигнал 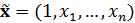келіп түседі және 
векторына 
жақындық өлшемі есептеледі 
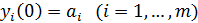және t =0 деп аламыз.
2. Екінші қабаттың әрбір -шы нейрон кірісіне 
векторы келіп түседі. Нейрондардың жаңа жағдайлары келесі формуламен есептеледі:
мұндағы 
. Аксондардың жаңа мәндері (белсенді функциясы): 
формуласымен есептелінеді, мұндағы 
3. Аксондардың тұрақтылығы тексеріледі: егер аксондар тұрақталса, яғни 
тең болса, онда барлық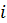 
үшін алгоритм өз жұмысын аяқтайды, кері жағдайда 2-ші пунктке қайта ораламыз.
3. Түс және түстік модельдер
үс ұғымы
Түс бейненің ақпараттық маңызын кӛтеруге және кӛрініс әсерін күшейту
құралы ретінде компьютерлік графикада ӛте маңызды орын алады. Түс жарық
шығаратын немесе шағылысатын объектілерден кӛзге түсетін жарықты
адамның миы талдау нәтижесінде қабылданады. Түстік рецепторлар әрқайсысы
тек бір ғана түсті қабылдайтын үш топқа бӛлінеді. Олар қызыл, жасыл және кӛк
түстер. Топтағы бір түстің жұмысының бұзылуы дальтонизмге – түсті дұрыс
қабылдамауға, түсті ажырата алмауға соқтыруы мүмкін.
Жарық ағыны үш «таза» спектрлі түстердің құрылымынан (қызыл, жасыл, кӛк –
ҚЖК) және олардың туындысынан құралады (ағылшын тіліндегі әдебиеттерде
(RGB – Red, Green, Blue қолданылады). Жарық шығаратын нысандар үшін
аддитивті түс шығару тән де, ал (жарық сәулелерінің қосындысымен)
шағылысатын нысандар үшін субтрактивті түс шығару (жарық сәулелері
алынады) тән. Бірінші типті нысанға мысал ретінде монитордың электронды-
сәулелі түтігін, ал екінші типке полиграфиялық баспаны айтуға болады. Жарық
ағындарының физикалық сипаттамасы қуаттылық, ашықтық және
жарықтандырылу параметрлерімен анықталады. Түстеудің визуалды
параметрлері жарықтығымен яғни жарықты әлсіз немесе күштерік шығаратын
аймақтарды ажыратумен сипатталады. Нысандардың жарықтығы бойынша
ажыратылатын ашық түстер арасындағы минималды айырмашылықты тоғыс
деп атайды. Тоғысу шамасы ашық түстер қатынасының логарифміне
пропорционал. Ашық түстер логарифмінде немесе оптикалық жазықтықта
берілген нысандардың оптикалық сипаттамаларының реті (ӛсу немесе кему
бойынша орналасқан) градацияны құрайды және бейнені ӛңдеу мен талдаудың
маңызды құралы болып табылады.
Компьютерлік графикада түстік кӛрсетілім ұғымын (басқаша атауы – түс
тереңдігі) қолданады. Ол оны монитор экранынан кӛрсету үшін түстік
ақпаратты кодтау әдісін анықтайды. Ақ-қара түсті бейнені алу үшін екі бит
жеткілікті. Ал сегіз разрядты кодтау түстердің 256 градациясын бейнелеуге
мүмкіндік береді. Екі байт (16 бит) 65536 реңді анықтайды (мұндай режим
High Color аталады) 24-разрядты кодтау әдісімен 16,5 миллионнан астам түсті
сипаттауға болады (бұл режим True Color аталады). Тәжірибе жүзінде
монитордың түстік кӛрсетіліміне түстік қамту ұғымы жақын.
Онымен қандай да бір шығару құрылғысының кӛмегімен түстер диапазонын
шығару түсіндіріледі (монитор, принтер және т.б.).
Бейнені аддитивті немесе субтрактивті әдістермен құру ұстанымдарына
сәйкес, түстік модельдер деп аталатын түс реңдерін құрамдас бӛліктерге бӛлу
тәсілі жасалған. Компьютерлік графикада негізінен RGB және HSB (аддитивті
бейнені құру мен ӛңдеуге арналған) сондай-ақ CMYK (бейне кӛшірмесін
полиграфиялық құралдармен басып шығаруға арналған) модельдері
қолданылады.
№10 ЕМТИХАН БИЛЕТІ
Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.
Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:
Бейнелерді тану теориясының негізгі есептері
Бейнелер сипатының типтері
Бейнелерді тану пәні XX ғасырдың басында Норберт Винер ашқан. Жаңа кибернетика пәні бейнелерді тану сұрағын зерттеуде сандық әдістерін енгізуге мүмкіндік берді. яғни, бейнелерді тану процесін математикалық әдістермен бейнелеуге көмектесті.
Тану есептерінде адамдың қатысуын ауыстырудың негізгі себептері:
- адамның бір типті операциялардан басқа маңыздырақ есептерді шығару үшін босатылуы;
- қабылданатын шешімдердің жылдамдығы мен сапасын арттыру.
20-шы жылдарда Р. Фишер жұмыстары дискриминантты талдауды тану пәнінің теориясы мен тәжірибесіндегі бір бөлімнің қалыптасуына әкелді.
40- шы жылдары А. Н. Колмогоров пен А. Я. Хинчин екі үлестіруді бөлу есебін қарастырды.
ХХ ғасырдың 50-60- шы жылдары көптеген еңбектер негізінде статистикалық шешімдер теориясы пайда болды. Мұның нәтижесінде жаңа объектті берілген класстардың біреуіне жатқызу алгоритмі табылды. Кибернетика шектерінде объектілерді тануға арналған құралдар мен әдістер зерттеле бастады. ЖАңа ғылыми пән "Бенелерді тану" атына ие болды.
Ары қарай тану теориясының математикалық аппараты келесілерді қолдану арқылы шешілді:
- Қолданбалы математика бөлімдерін; ақпарат теориясын;
- логика алгебрасының әдістерін;
- математикалық программалау мен системотехниканы.
70-шы жылдар ортасында тану өзіңдік ғылыми бағыт ретінде толығымен қалыптасты, Бейнелерді танудың математикалық теориясын жасау мүмкіндігі пайда болды.
Сызықтық функция
y = kx + l (мұндағы x - тәуелсіз айнымалы, k мен l – нақты сандар) түріндегі формуламен берілетін фуннкцияны сызықтық функция деп атайды.
у = kx + l функциясының анықталу аймағы барлық нақты сандар жиыны.
Егер у = kx + l сызықтық функциясындағы l = 0 болса, онда у = kx түрінде жазылады. у = kx функциясы тура пропорционалдық деп аталады.
Егер у = kx + l формуласындағы k = 0 болса, у = 0x+l, онда у = l; у = l функциясы тұрақты функция деп аталады. у = l тұрақты функциясы сызықтық функцияның дербес жағдайы.
Сызықтық функцияның графигі
У = 1,5x - 2 сызықтық функциясының графигін сызайық.
Ол үшін x пен y-тің сәйкес мәндерінің кестесін құрастыру керек.
| х | -3 | -2 | -1 | ||||
| у | -6,5 | -5 | -3,5 | -2 | -0,5 | 2,5 |
Координаталық жазықтықта координаталары кестеде көрсетілген нүктелерді белгілейік.
Белгіленген нүктелерді қоссақ, түзу сызылады. Осы түзу у = 1,5x - 2 сызықтық функциясының графигі болады. y = kx + l функциясының графигі түзу сызық.
Жазықтықтағы екі нүкте арқылы бір ғана түзу жүргізілетіндіктен, түзуді жүргізу үшін, оның екі нүктесінің координаталарын білу жеткілікті.
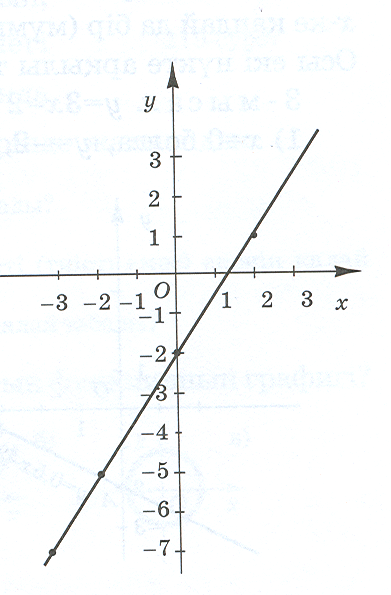Y = kx + l сызықтық функциясының графигі болатын тузу ординаталар (Оу) осін (0;l) нүктесінде, ал абциссалар (Ох) осін (
;0) нүктесінде қияды.
Сызықтық функцияның дербес жағдайлардағы графигі
l=0 және k 0 болғанда у=kx тура пропорционалдығының графигін қарастырайық.
у=kx функциясыныңформуласынндағы х =0 болғанда у =0. Сондықтан оның графигі координаталар басы арқылы өтеді.
у=kx (мұндағы k 0) функциясының графигі координаталар басы арқылы өтетін түзу.
у=kx тура пропорционалдығының графигін салу үшін ізделінді нүктелердің бірі ретінде О(0;0) нүктесін алу керек.
Ізделінді екінші нүктенің координаталарын табу үшін x-тің нөлден өзгеше қандай да бір (мүмкін) мәнін қойып, оған сәйкес у- тін мәнін табу керек.
Мысалы, у=2х функциясы үшін, х=2 болғанда у=4. А(2;4) нүктесін алу керек. Табылған О(0;0) және А(2;4) нүктелері арқылы жүргізілген түзу у=2х функциясының графигі.
у=kx функциясы графигінің координаталық жазықтықтағы орналасуы к коэфицентіне тәуелді. у=kx функциясында, егер х=1 болса у=k.
у=kx функциясының графигі –О(0;0) және (1;к) нүктелері арқылы өтетін түзу.
Егер к 0 болса, у=kx функциясының графигі I және IIIкоординаталық ширектерде, ал k 0 болса, II және IV координаталық ширектерде орналасады.
у=kx функциясының графигі мен у=kx+l функциясының графигі k- ның бірдей мәнінде өзара параллель түзулер. х-тің кез келген мәні үшін у = kx+ l функциясының мәні у=kx функциясының мәнінен l-ге артық.
у = kx+l функциясындағы к=0 болса, функция у=l формуласы-мен жазылады. у=l формуласының графигі абциссалар осіне параллель, абциссасы 0; ординаталары l болатын түзу.
920 жылы түстік кеңістік моделі СІЕLab (Communication International del Eclairage – жарықтандыру бойынша халықаралық комиссия. L,a,b – осы жүйедегі координаталар ӛсінің белгіленуі) жасалады. CIELab моделінде кез келген түс жарықтығымен (L) және хроматикалық құрамымен: жасылдан қызылға дейін ӛзгеретін диапазон параметрімен (a), және кӛктен сарыға дейін ӛзгеретін диапазон параметрімен (b) анықталады. CIELab моделінің түсті қамтуы баспа құралдары мен монитор мүмкіндіктерінен біршама асып түседі, сондықтан бұл модельмен бейнені баспаға шығармас бұрын оны түрлендіріп алуға тура келеді. Аталмыш модель түрлі-түсті химиялық процестерді полиграфиялық процестермен үйлестіру үшін жасалған болатын. Бүгінге ол Adobe Photoshop программасы үшін бірауыздан мақұлданған стандарт болып табылады.
Билет
Бейнелерді тану пәні. Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.
Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:
· символдарды тануда (баспа және жазба мәтіндерінде, банк чектерінде және т.б.);
· әртүрлі жиілік диапазонда (оптикалық, инфрақызыл, дыбыстық, радиожиілікті) алынған бейнелер мен сахнаны талдауда;
· медициналық диагностикада;
· қауіпсіздік жүйелерінде;
· дыбыстарды тануда;
· деректер қорында және білімде (сонымен қатар, Интернет-ресурстарында) іздеу және классификациялауда, кластеризациялауда қолданылады.
Бейнелерді тану теориясының негізгі есептері. Сандарды, әріптерді және т.б. символдарды тануды іске асыратын техникалық жүйе мысалында бейнелерді тану теориясының негізгі есептерін қарастырайық. Мұндай жүйе 60-жылдары АҚШ-да жасалған және ұзақ уақыт бойы конвертті символдарды тану үшін қолданылған.
Мысалы, тану жүйесінің кірісіне қағаз лентада жазылған қандай да бір х символы келіп түссін және осы символды тану керек болсын. Тану керек объектілерді бейне («pattern») деп атайды. Солдан оңға қарай жылжитын есептеуші басы бар техникалық жүйе 
уақытына тәуелді боялған бет ауданының өзгерісін 
жылдамдығы өлшейді (1.1-сурет). символ-бейнесінің функциясы оның бейнеленуі болып табылады. Сигналды уақыттың дискретті нүктелерінде өлшесек, х символын х векторы түрінде аламыз. функциясын функциялар кеңістігінде элемент-вектор деп есептей аламыз. Бір түрден екінші түрге ауысу, ереже бойынша, бейне туралы ақпараттар санын азайтады.
Сурет 1.1
Кіріс х символ-бейнесі 
кластар жиынының қандай да бір класына жатуы мүмкін - әрбір класс қандай да бір символға (әріпке, санға және т.б.) сәйкес келеді. Кластарды бір-бірімен қиылыспайды деп аламыз.
| Оқыту |
| Белгілерді таңдау |
| Классификатор |
| Бейнені векторлық форма түрлендіру |
Сурет 1.2 Бейнелерді тану жүйесінің жалпы сызбасы
Бейнелерді тану есебі х бейнесінің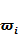 
кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады. Егер бейне метрикалық кеңістіктің элемент-векторы болса, бейнені класқа жатқызуды, мысалы, вектор мен класс арасындағы қашықтықты есептеу көмегімен іске асыра аламыз. Классификатор шығысында кіріс бейнесінің қай класқа (класс номерін) жататындығын немесе ешқандай класқа жатпайтындығын анықтауымыз қажет.
Бейненің векторлық формаға түрлендіру бөлімімен классификатор арасында кішкене санды таңдау бөлімі (мысалы, 
аналогты сигналының х векторына түрленуі) болуы мүмкін. Мұндай бөлімнің болуы вектор өлшемін азайтып, тану жүйесінің жылдамдығын арттырады.
Жалпы, тану жүйесінде оқыту бөлімі болуы мүмкін. Бұл бөлім оқытылатын бейнелерді таңдау кезінде классификация ережесін қалыптастыруға мүмкіндік береді. Сонымен қатар, оқытылатын бейнелер бойынша ақпараттық белгілерді таңдау ережесі қалыптасады.
Жоғарыда қарастырылған мысалды және тану сызбасын талдай отырып, келесі бейнелерді тану теориясының негізгі есептерін ерекшелеуге болады:
11. Бейнелердің математикалық сипатталуы. Бейнелерді математикалық сипаттаудың ең тиімді әдісінің бірі - бейнелерді векторлық сипаттау болып табылады. Бұл жағдайда әрбір х бейнесіне сәйкесінше Х векторлық кеңістігінің элементі, яғни осы бейненің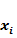 
белгілерінің қандай да бір x= 
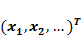векторы сәйкес келеді. Мұндай векторлық кеңістік белгілер кеңістігі деп аталады. Ереже бойынша, бұл кеңістік шекті өлшемді және метрикалық болып табылады. Егер бұл кеңістіктің белгілері нақты шамалар болса, онда мұндай кеңістік 
метрикалық кеңістігіне изоморфты, ал n – белгілер кеңістігінің өлшемі болып есептеледі.
Кейбір тану есептерінде (мысалы, суреттерді тануда) белгілер векторының әртүрлі ұзындығы болуы мүмкін.
12. Берілген бейнені сипаттайтын ақпараттық белгілерді таңдау. Бұл бейнелерді тану теориясында негізгі және маңызды есептердің бірі – берілген тану есебінде бейнелерді нақтырақ сипаттайтын, белгілердің минималды санын анықтау болып табылады.
Белгілерді тану үшін толық таңдау жиынын белгілер алфавиті, ал тану есебінің берілген класы үшін жеткілікті ең аз белгілер жиынын белгілер сөздігі деп атайды. Белгілер сөздігі белгілер алфавитінің ішкі жиыны болмауы да мүмкін, яғни ол белгілер алфавиті элементінің кейбір функцияларынан тұруы да мүмкін. Жалпы жағдайда, жүйе белгілер сөздігін өзі анықтау қажет.
13. Танылатын бейнелердің кластарын сипаттау. Бұл есеп кластардың шекараларын анықтайды. Кластар шекаралары тану жүйесінің жасалу кезеңінде нақты берілуі мүмкін немесе жүйе өзінің жұмысы барысында өзі табуы керек.
14. Тиімді шешуші әдістерді табу, яғни бейненің белгілер векторын қандай да бір класқа жатқызу керек.
15. Бейнелерді классификациялаудың нақтылығын бағалау. Шешім қабылдайтын адам немесе техника бейнені қандай-да бір класқа жатқызу арқылы классификацияның қателігіне байланысты қателік шамасын бағалай алу қажет.
Бейнелер сипатының типтері. Белгілердің сипаты негізгі үш типімен ерекшеленеді:
1. Физикалық түрде сипатталуы, мысалы, әртүрлі датчиктерден алынған көрсеткіштер. Физикалық түрде сипатталуы детерминирленген және ықтималдылықты болуы мүмкін және бұл сипатталуды векторлар көмегімен сипаттап, векторлық кеңістіктің элементтері ретінде қарастыруға оңай болады.
2. Сапалы түрде сипатталуы. Сапалы түрде сипатталуда “ашық”, “жоғары”, “төмен” және т.б. түсініктер мысал бола алады. Мұндай сипаттамалар бұлдыр жиындар теориясы әдістерінің лингвистикалық айнымалылар көмегімен сипатталуы мүмкін.
3. Құрылымдық түрде сипатталуы. Бұл сипатталу күрделі объектілер (1.3-сурет) немесе сахналардың бейнелерін сипаттау үшін қолданылады. Құрылымдық сипаттауда формальды тіл - графтар теориясы (1.4-сурет) болып табылады.
4. Логикалық түрде сипатталуы – бұл ақиқат немесе жалған болатын сөйлем болып табылады.
Сурет 1.3 Сурет 1.4
Тану жүйесінің типтері. Тану жүйесі классификациясының бірнеше критерийлерін ерекшелеуге болады. Мұндай критерийлердің бірі – белгілер туралы ақпараттар сипаттамасы:
· детеминирленген;
· ықтималданған;
· логикалық;
· құрылымдық;
· құрастырылған.
Келесі критерий – танылатын объектілер жөнінде алдын-ала деректемелі ақпарат санын алуға болады. Тану жүйесінің үш негізгі типтері бар.
4. Оқытусыз жүйелер. Алдын-ала деректемелі ақпараттар саны белгілер алфавитін, белгілер сөздігін қалыптастыруға және кластар шекараларын анықтауға жеткілікті. Бұл жағдайда тану жүйесінде (1.2-сурет) «оқыту» бөлімі болмайды.
5. Оқытушымен оқытуға негізделген жүйелер. Алдын-ала деректемелі ақпараттар саны тек белгілер алфавитіне және белгілер сөздігін қалыптастыру үшін ғана жеткілікті. Тану жүйесіне оқытатын жиындар (оқытатын таңдаулар) деп аталатын қандай да бір объектілер жиыны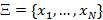 
ұсынылады және осы объектілердің қай класқа жататындығын көрсетеді. Дұрыс емес классификациялау қателігін жіберудің ең аз шарты орындалу үшін жүйе классификация ережесінің параметрлерін өзі тұрғызу керек. Мысалы, (1.5-сурет) оқытатын таңдаудағы объектілер жиынын екі түзу арқылы 
объектілері бірінші класқа жататындай,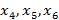 
объектілері екінші класқа жататындай, ал 
үшінші класқа жататындай етіп бөлуге болады.
Сурет 1.5 Сурет 1.6
6. Өз бетінше оқуға негізделген жүйелер. Алдын-ала деректемелі ақпараттар саны белгілер сөздігін қалыптастыру үшін де жеткіліксіз. Сондықтан бейнелерді тану жүйесіне бейнелерді тану есебін түсіндіретін ережелер тізімі енгізіледі. Бұл ережелер тізімі осы облыста білімі бар эксперт-мамандарымен жасалады және мұндай жүйелерді эксперттік (интеллектуалды) жүйелер деп атайды. Ережелер жиыны нәтижесінен тану жүйесі белгілер сөздігі мен класс шекараларын өзі құру керек және мәліметтерді өңдеу үшін логика-лингвистикалық әдістер қолданылады. Мұндай жүйе көбінесе медициналық диагностикада қолданылады. Мысалы, кардиолог дәрігерлері үшін тану жүйесі (1.6-сурет), мұндағы a(t) - уақытқа байланысты жүрек соғысы амплитудасының өзгеруі.
3сурак RGB түстік моделі
Компьютерлік графикада түс әртүрлі түстік модель мен түстік кеңістікте беріледі. Оның әрқайсысы экранда көрсетілуге немесе басып шығаруға негізделіп, жекелей таңдалады. Түстік кеңістік бейнені шығару құрылғылары мен құжатты экспорттау мен импорттау барысында қолданылады.
Егер басылым полиграфиялық басып шығаруға арналса,онда түстік кеңістік CMYK форматында, ал экранда көрсету үшін қарастырылса RGB таңдалуы тиіс. Adobe Indesing өзінде RGB, CMYK және Lab модельдері бар болса, импортталған бейнелерде HSB немесе Web Safe RGB болады. Сонымен қатар Grayscale моделі де жиі қолданылады.
Дәстүр бойынша бейнелер RGB моелінде өңделеді – Red (Қызыл), Green (Жасыл), Blue (Көк). Сондықтан бұл модель монитор түстеріне сәйкес келетіндіктен осы қолданысқа ыңғайлы болып келеді.
2.16 - сурет. RGB түстік моделіндегі түстердің түрленуі
Ал басып шығару барысында 4 түстік модель қолданылады: көк, күлгін, сары және қара. Сондықтан RGB моделіндегі бейнені басып шығару кезінде CMYK режиміне түрлендірілуі тиіс.
№12 ЕМТИХАН БИЛЕТІ
Тану сызбасын талдай отырып, келесі бейнелерді тану теориясының негізгі есептерін ерекшелеуге болады:
16. Бейнелердің математикалық сипатталуы. Бейнелерді математикалық сипаттаудың ең тиімді әдісінің бірі - бейнелерді векторлық сипаттау болып табылады. Бұл жағдайда әрбір х бейнесіне сәйкесінше Х векторлық кеңістігінің элементі, яғни осы бейненің белгілерінің қандай да бір x= векторы сәйкес келеді. Мұндай векторлық кеңістік белгілер кеңістігі деп аталады. Ереже бойынша, бұл кеңістік шекті өлшемді және метрикалық болып табылады. Егер бұл кеңістіктің белгілері нақты шамалар болса, онда мұндай кеңістік метрикалық кеңістігіне изоморфты, ал n – белгілер кеңістігінің өлшемі болып есептеледі.
Кейбір тану есептерінде (мысалы, суреттерді тануда) белгілер векторының әртүрлі ұзындығы болуы мүмкін.
17. Берілген бейнені сипаттайтын ақпараттық белгілерді таңдау. Бұл бейнелерді тану теориясында негізгі және маңызды есептердің бірі – берілген тану есебінде бейнелерді нақтырақ сипаттайтын, белгілердің минималды санын анықтау болып табылады.
Белгілерді тану үшін толық таңдау жиынын белгілер алфавиті, ал тану есебінің берілген класы үшін жеткілікті ең аз белгілер жиынын белгілер сөздігі деп атайды. Белгілер сөздігі белгілер алфавитінің ішкі жиыны болмауы да мүмкін, яғни ол белгілер алфавиті элементінің кейбір функцияларынан тұруы да мүмкін. Жалпы жағдайда, жүйе белгілер сөздігін өзі анықтау қажет.
18. Танылатын бейнелердің кластарын сипаттау. Бұл есеп кластардың шекараларын анықтайды. Кластар шекаралары тану жүйесінің жасалу кезеңінде нақты берілуі мүмкін немесе жүйе өзінің жұмысы барысында өзі табуы керек.
19. Тиімді шешуші әдістерді табу, яғни бейненің белгілер векторын қандай да бір класқа жатқызу керек.
20. Бейнелерді классификациялаудың нақтылығын бағалау. Шешім қабылдайтын адам немесе техника бейнені қандай-да бір класқа жатқызу арқылы классификацияның қателігіне байланысты қателік шамасын бағалай алу қажет.
Дата добавления: 2015-08-26; просмотров: 389 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторлы графика форматы | | | Байес формуласы 1 страница |