Байес формуласы 4 страница

Класс (class) — қолдаңылатын қасиеттерінің немесе өңдеу төсілдерінің ортақтылығын сипаттайтын объектілердің жиынтығы.
Класс үлгісі (экземпляр класса; class instance) — кейбір класс конструкторы жасаған нақтылы объектіні белгілейтін объектілік-бейімделген программалау термині.Класс үлгісінің класта анықталған немесе түп кластардан мұралық иемденген объекті мен әдіске тән мәліметтерді сақтайтын қасиеті бар.

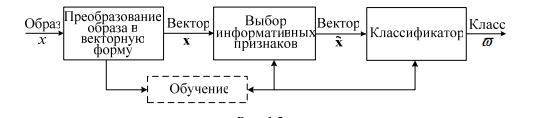
Бейнелерді тану есебі х бейнесінің 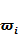кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады. Егер бейне метрикалық кеңістіктің элемент-векторы болса, бейнені класқа жатқызуды, мысалы, вектор мен класс арасындағы қашықтықты есептеу көмегімен іске асыра аламыз. Классификатор шығысында кіріс бейнесінің қай класқа (класс номерін) жататындығын немесе ешқандай класқа жатпайтындығын анықтауымыз қажет.

Бейнелерді тану пәні. Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.

Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:

· символдарды тануда (баспа және жазба мәтіндерінде, банк чектерінде және т.б.);

· әртүрлі жиілік диапазонда (оптикалық, инфрақызыл, дыбыстық, радиожиілікті) алынған бейнелер мен сахнаны талдауда;

· медициналық диагностикада;

· қауіпсіздік жүйелерінде;

· дыбыстарды тануда;

· деректер қорында және білімде (сонымен қатар, Интернет-ресурстарында) іздеу және классификациялауда, кластеризациялауда қолданылады.

2. Бірінші әдіс - бейне мен класс центрі арасындағы қашықтықты анықтау. Бұл әдісті бір эталонды бейне – класс центрімен сипатталған кезде және дұрыс емес классификациялауда қателік құны көп емес жағдайларда қолдану тиімді. Бұл әдісті белгілер кеңістігіндегі бір класта орналасқан бейне-векторлардың бір-біріне өте жақын орналасуы қажет. Осы жағдайда қашықтықты анықтау келесі қадамдардан тұрады:

c) класының центрлері анықталады:

яғни класс центрі дегеніміз- класс нүктелерінің арифметикалық ортасы болып табылады. Егер тануды оқытумен қарастыратын болсақ, онда келтірілген жоғарыдағы формулада оқытылатын таңдаудағы элементтер болып сол класқа нақты жататын элементтердің қосындысы қарастырылады.

d) бейнесі мен класы арасындағы қашықтық бейне мен класс центрі арасындағы қашықтық ретінде қарастырылады: 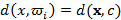. Мысалы, және

Екінші әдіс - жақын көршілер әдісі. Бұл әдісте қашықтықты есептеу келесі қадамдардан тұрады:

c. элементін анықтаймыз, яғни

.

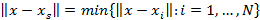d. шарт тексеріледі: егер болса, онда жатады деп есептеледі. Бұл жағдайда қашықтық функциясы келесі формуламен анықталады

.

Бұл әдіс дұрыс емес классификациялау нәтижесінде қателікті жіберу мүмкіндігі жоғары, сондықтан берілгендердегі қателік аз болған жағдайда қолданылады.

Егер облысында қиылыспайтын облыстары бар болса, онда белгілер кеңістігін болатындай жеке облыстарға бөлеміз. Мұндай облыстарды Воронов облыстары (немесе Дирихле облыстары) деп атайды.

Үшінші әдіс - эталондық бейнеге дейінгі қашықтықты анықтау. Бұл әдіс бір эталонды бейне – класс центрімен анықтау қиын болған жағдайда қолданылады және эталон бейнесін енгізу мен кластың құрылымдық немесе геометриялық қасиеттерін білуге негізделген. Мұндай жағдайдың белгісі болып класс элементтері дисперсиясының үлкен мәні болып саналады. Сонымен қатар таңдалатын оқытудағы кейбір элементтер жиыны ерекшеленеді (эталондық бейнелер деп аталатын). Мұндай біртекті құрылымдар бір эталонды бейненің шеңберінде жинақталады және ол кластер деп аталады.

Егер эталондық бейнелер белгілі болып, класс элементтері бірнеше эталондық бейнелерді айналдыра жақсы топтастырылса, онда берілген және класы арасындағы қашықтық келесі формула бойынша анықталады:

мұндағы - класының эталондық бейне-векторы.

Кластың эталондық бейнелерін табу есебі осы класта қайталанатын құрылымды ерекшелеумен және олардың центрін табумен шешіледі. Қайталанатын құрылымдар нақты қайталану критерийлерін қанағаттандыратын векторлар жиынын ұсынады. Мұндай құрылымдарды кластерлер, ал құрылымды табу есебін – кластеризация есебі деп атайды. Оқыту таңдауын кластерге бөлу есебін кластеризация деп атаймыз.

Ескерту. Кейбір есептерде және кластар арасындағы қашықтығын есептеу керек. Бұл қашықтықты мақсатына, кластар құрылымына және дұрыс емес шешу құнына байланысты түрлі жолдармен анықтауға болады. Кластар арасындағы қашықтықты келесі әдістермен есептеуге болады:

5. екі элемент арасындағы минималды қашықтық, әр элемент сәйкесінше өз класына жатады;

6. барлық элементтер жұбы арасында орташа қашықтықты табу, әр элемент өз класына жатады, мұндағы кластар арасындағы барлық элемент жұптарының жиыны;

7. элемент жұптары арасындағы максималды қашықтық, әр элемент өз класына жатады;

8. кластары арасындағы қашықтық, мұндағы кластырының сәйкесінше центрлері.

3. Үш өлшемді таратылым экранда қос бейне ретінде көрсетілсе, 3D бейнені түзету үшін қос бейненің түрін таңдаңыз. s (Реттеу) пәрменін таңдап, 3D пішімін таңдаңыз және қос бейненің позицияларына сай Қоян-қолтық («Side by side») немесе Жoғары/төмен («Top/ bottom») параметрін таңдаңыз

Билет

.Бейнелерді тану есептерінің негізгі есептері.

Бейнелерді тану теориясының негізгі есептері. Сандарды, әріптерді және т.б. символдарды тануды іске асыратын техникалық жүйе мысалында бейнелерді тану теориясының негізгі есептерін қарастырайық. Мұндай жүйе 60-жылдары АҚШ-да жасалған және ұзақ уақыт бойы конвертті символдарды тану үшін қолданылған.

Мысалы, тану жүйесінің кірісіне қағаз лентада жазылған қандай да бір х символы келіп түссін және осы символды тану керек болсын. Тану керек объектілерді бейне («pattern») деп атайды. Солдан оңға қарай жылжитын есептеуші басы бар техникалық жүйе уақытына тәуелді боялған бет ауданының өзгерісін жылдамдығы өлшейді (1.1-сурет). символ-бейнесінің функциясы оның бейнеленуі болып табылады. Сигналды уақыттың дискретті нүктелерінде өлшесек, х символын х векторы түрінде аламыз. функциясын функциялар кеңістігінде элемент-вектор деп есептей аламыз. Бір түрден екінші түрге ауысу, ереже бойынша, бейне туралы ақпараттар санын азайтады.

Бейнелерді тану есебі х бейнесінің 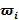кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады.

1. Бейненің математикалық сипатталуы. Бейнені математикалық сипаттаудың ең тиімді әдісінің бірі бейнеерді вектордың сипаттау болып таылады. Бұл жағдайда әрбәр х бейнесіне сәйкесінше х векторының кеңістігінің лементтерінің, яғни осы бейненің 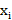белгілерінің қандай да бір сәйкес келеді. Яғни векторлық кеңістікті белгілер кеңістік деп аталады.Ереже бойынша бұл кеңістің шекті өлшемді,яғни математикалық б-п т-ды. Егер бұл кеңстіктің белгілері жақты шамалары болса, онда мұндай кеңістік матем-к кең-ке изомаорфты, ал n-белгілер кеңістіктің өлшемі.

2. Берілген бейнені сипаттайтын ақпараттық белгілерді таңдау. Бұл бейнелерді тану теориясында негізгі және маңызды есептердің бірі – берілген тану есебінде бейнелерді нақтырақ сипаттайтын, белгілердің минималды санын анықтау болып табылады.

3. Танылатын бейненің кластарын сипаттау. Бұл есеп жүйесінің жасауы кезінде нақты берілуі мүмкін немесе жүйе өзінің жұмысы барысын да өзі табуы керек.

4. Тиімді шешуші әдістерді табу. Яғни, бейненің белгілері векторының қандай да бір класқа жатқызу керек.

5. Бейнелерді құрудың нақтылығын бағалау. Шешім қабылдайтын адам немесе техника бейнені қандай да бір кл-қа жатқызу арқылы кл-ның қателігіне б-ты қателік шамасын бағалай алу қажет.

21.2. Максимумды арақашықтық алгоритмі.

Максиминдік қашықтық принципіне негізделген алгоритм евклидтік қашықтықты қолданатын тағы да бір эвристикалық әдіс. Бұл алгоритмнің түсіндірілуін келесі мысал түрінде қарастырайық:

Екі өлшемді бейнелерден тұратын он элементті іріктеуге алайық:

Объектінің кез келген біреуі, мысалы, – бірінші кластер центрі деп алайық .

Осы бейнесінен ең алыс орналасқан элементті тауып, мысалы элементі болсын және бұл элементті екі кластер центрі деп аламыз .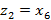

Қалған бейнелер мен 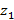және кластер центрлері арасында қашықтық есептелініп, әрбір жұп үшін минималды мән таңдалады.

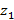X=min (, ), , Y=min(, ),

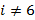
осы екі минималды мәннен үшінші кластердің центрін аламыз:

X₃= max(X,Y)

Егер, соңғы есептелген қашықтық 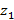және кластерлер центрінен едәуір қашықтықта орналасса, онда -ке сәйкестендірілген бейне оның центрі болып есептеледі.

Әрбір үш қашықтық топ арасында минимум мән таңдалады және минимум мәндер ішінде максимум мән элементтердің орта мәнінен үлкен болса, онда ол келесі кластер центрі болады.

Нәтижесінде кластер центрлері және { }, { }, { } жиындары анықталады.

21.3.Деформация және олардың түрлері

Interactive Distontion (Интерактивті деформания жәе шығару) «өткір деформацияы» құмарларға арналған, сондай-ақ оның көмегімен объектілер түгел танымастай етіп түрленеді. Бұрмалаудың 3 түрі бар:

1) Қысылу және ілгері шығу бұрмалануы

2) Түймелік (зигзаг) бұрмалау

3) Бұрап қою арнналған бұрмалау

Атрибуттар тақтасында келесі батырмалар:

- Түймелік бұрмалаудың ауытқу еі

- Т-к бұр.-у жиілігі

- Кездейсоқ бұрмалау

- Жергілікті бұрмалауы

- Қисыққа түрлендіру

- Сағат тілі және сағат тіліне қарсы

- Бұрмалау ортасы

- Толық айналымдар

Бұл құрал Property Bar құралдың жалағымен бірге жұмыс істейді, онда деформацияның 3 типі ұсынылған: Pull (тарт және интер) Zipper (зигзаг) Thister (бұралу)

Билет

1111.Бейнелер сипатының типтері. Белгілердің сипаты негізгі үш типімен ерекшеленеді:

9. Физикалық түрде сипатталуы, мысалы, әртүрлі датчиктерден алынған көрсеткіштер. Физикалық түрде сипатталуы детерминирленген және ықтималдылықты болуы мүмкін және бұл сипатталуды векторлар көмегімен сипаттап, векторлық кеңістіктің элементтері ретінде қарастыруға оңай болады.

10. Сапалы түрде сипатталуы. Сапалы түрде сипатталуда “ашық”, “жоғары”, “төмен” және т.б. түсініктер мысал бола алады. Мұндай сипаттамалар бұлдыр жиындар теориясы әдістерінің лингвистикалық айнымалылар көмегімен сипатталуы мүмкін.

11. Құрылымдық түрде сипатталуы. Бұл сипатталу күрделі объектілер (1.3-сурет) немесе сахналардың бейнелерін сипаттау үшін қолданылады. Құрылымдық сипаттауда формальды тіл - графтар теориясы (1.4-сурет) болып табылады.

12. Логикалық түрде сипатталуы – бұл ақиқат немесе жалған болатын сөйлем болып табылады.

Сурет 1.3 Сурет 1.4

Тану жүйесінің типтері. Тану жүйесі классификациясының бірнеше критерийлерін ерекшелеуге болады. Мұндай критерийлердің бірі – белгілер туралы ақпараттар сипаттамасы:

· детеминирленген;

· ықтималданған;

· логикалық;

· құрылымдық;

· құрастырылған.

Келесі критерий – танылатын объектілер жөнінде алдын-ала деректемелі ақпарат санын алуға болады. Тану жүйесінің үш негізгі типтері бар.

7. Оқытусыз жүйелер. Алдын-ала деректемелі ақпараттар саны белгілер алфавитін, белгілер сөздігін қалыптастыруға және кластар шекараларын анықтауға жеткілікті. Бұл жағдайда тану жүйесінде (1.2-сурет) «оқыту» бөлімі болмайды.

8. Оқытушымен оқытуға негізделген жүйелер. Алдын-ала деректемелі ақпараттар саны тек белгілер алфавитіне және белгілер сөздігін қалыптастыру үшін ғана жеткілікті. Тану жүйесіне оқытатын жиындар (оқытатын таңдаулар) деп аталатын қандай да бір объектілер жиыны ұсынылады және осы объектілердің қай класқа жататындығын көрсетеді. Дұрыс емес классификациялау қателігін жіберудің ең аз шарты орындалу үшін жүйе классификация ережесінің параметрлерін өзі тұрғызу керек. Мысалы, (1.5-сурет) оқытатын таңдаудағы объектілер жиынын екі түзу арқылы объектілері бірінші класқа жататындай, 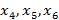объектілері екінші класқа жататындай, ал үшінші класқа жататындай етіп бөлуге болады.

Сурет 1.5 Сурет 1.6

Өз бетінше оқуға негізделген жүйелер. Алдын-ала деректемелі ақпараттар саны белгілер сөздігін қалыптастыру үшін де жеткіліксіз. Сондықтан бейнелерді тану жүйесіне бейнелерді тану есебін түсіндіретін ережелер тізімі енгізіледі. Бұл ережелер тізімі осы облыста білімі бар эксперт-мамандарымен жасалады және мұндай жүйелерді эксперттік (интеллектуалды) жүйелер деп атайды. Ережелер жиыны нәтижесінен тану жүйесі белгілер сөздігі мен класс шекараларын өзі құру керек және мәліметтерді өңдеу үшін логика-лингвистикалық әдістер қолданылады. Мұндай жүйе көбінесе медициналық диагностикада қолданылады. Мысалы, кардиолог дәрігерлері үшін тану жүйесі (1.6-сурет), мұндағы a(t) - уақытқа байланысты жүрек соғысы амплитудасының өзгеруі. Бейнелерді тану жүйесінде құрылымдық әдіс бейнелерде акырындап және тізбектей қозғала отырып қажетті ақпаратты жинайды. Необходимость в выделении отдельных символов для их распознавания отпадает, так как в процессе анализа полученных на данный момент сведений об изображении распознаватель может выбирать область дальнейшего исследования и самостоятельно определять границы наблюдаемого символа. В настоящее время структурные методы распознавания изображений применяются в наиболее развитых системах распознавания скорописного текста.

9. Нейрондық желі және Хопфилд оқыту алгоритмі. Хэмминг алгоритмі және нейрондық желіні оқыту.

Нейроинформатика негізінде екі түсінік бар: мидың құрылымы және оны оқыту процестері. Мидың құрылымын қарастыру кезінде қарапайым элемент –«нейрон» негізгі түсінігі болып табылады. Екінші түсінік: нейрондар арасындағы байланысты оқытуда қалыптасатын нейрондар желісі көмегімен нақты есепті шеше алу керек. Қарапайым нейрондық желі болып персептрон есептеледі.

Нейрондық желі тікелей программалауды, яғни нақты ережелер бойынша байланысты қалыптастыру, сонымен қатар нейрондық желіні нақты бір есептерге бағыттау. Бұл процесс оқыту деп аталады.

Оқыту «мадақтау-жазалау» принципі бойынша құрылады: жүйеге жауабы бар мысалдар жиыны ұсынылады. Нейрондар кіріс сигналдарын түрлендіреді, жауабын да сигналдар жиынымен береді. Дұрыс жауаптан ауытқу желінің ішкі жөндеулерін өзгерту жолымен қайтарады. Бұл оқытудың ерекшелігі - ауытқудың минимизациялауында.

Стандартты формальды нейрон кіріс сумматорынан, сызықты емес түрлендіруден және шығысындағы тармақталудан тұрады. Нейронның маңызды элементі болып адаптивті сумматор болып есептеледі. Адаптивті сумматор кіріс векторының 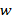өзгертуші параметріне скалярлы көбейтіндісін есептейді.

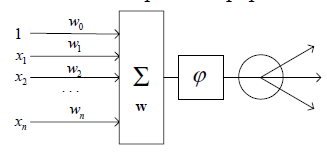
Сурет -1

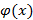Сигнал ары қарай сызықты емес түрлендірушіге келіп түседі және ол қүшейту функциясы деп аталады. Функция скалярлы сигналын сигналына түрлендіреді (нейронның шығысын аксон деп атайды). Тармақтау нүктесі бір сигналдың бірнеше адрестері бойынша жіберілуін қамтамасыз етеді.

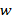Сызықты байланыс (синапс) сумматордан жеке кездеспейді. Синапс кіріс сигналын «синапс салмағына» көбейтеді.

Нейрондық желі жиындары арасында екі базалық құрылымды ерекшелеуге болады - қабатталған және толық байланысқан желілер.

Қабатталған желілерде нейрондар бірнеше қабаттарда орналасқан. Бірінші қабаттағы нейрондар кіріс сигналдарын қабылдап, түрлендіреді және тармақтау нүктесі арқылы екінші қабаттағы нейрондарға жібереді. Сол сияқты екінші қабат өңделіп, шы қабатқа дейін жетеді, және шығыс сигналдарын береді.

Толық байланысқан желілерде әрбір нейрон өзінің шығыс сигналын басқа нейрондарға өзімен қосып жібереді. Желінің шығыс сигналдары барлық немесе кейбір шығыс сигналдары болуы мүмкін. Кіріс сигналдардың барлығы барлық нейрондарға жіберіледі.

Нейрондық желілер сызықты және бір айнымалысы бар сызықты емес функцияларды есептей алады, сонымен қатар барлық желілердің каскадты бірігуінде алынатын функциядан функцияға суперпозицияларын есептей алады.

Хопфилд нейрондық желісі ассоциативті жады желісіне жатады, яғни бұл желілер қандай-да бір ақпаратты бейне түрінде сақтайды және кірісінде сол бейнені еске түсіреді. Кіріс векторы биполярлы болуы тиіс, яғни 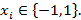Әрбір ұсынылған векторы үшін хопфилд нейрон желісі оған ең жақын эталон-бейне тауып, оны шығысында береді. Векторлар биполярлы болғандықтан векторы мен 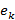эталонды вектор арасындағы қашықтық квадраты 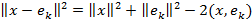тең. Онда 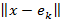қашықтығы минималды болады сонда тек сонда ғана, егер 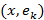скалярлы көбейтіндісі максималды болса. Хопфилд желісінің функционалдау негізінде энергия функционалын минимизациялау идеясы жатыр, яғни

Дата добавления: 2015-08-26