Точечные оценки дисперсии.

А. Если производятся измерения известной величине а (эталона), то в качестве эффективной оценки дисперсия применяют средний квадрат отклонения результатов измерений х₁, х₂, … х_п от значения а:

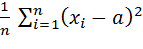= , (1)

Б. Если измеряют неизвестную величину, то в качестве оценки дисперсии применяют эмпирическую дисперсию

, (2)

где - среднее арифметическое значение результатов измерений. Оценка (2) является несмещенной и состоятельной, но не является эффективной (она является лишь асимптотически эффективной, т. е. ее рассеяние стремится к минимальному при неограниченном увеличении числа измерений п).

В. Если одним и тем же прибором производят m серий измерений (вообще говоря, различных величин), то в качестве оценки дисперсии применяют взвешенное среднее из эмпирических дисперсий

, (3)

где n₁, n₂,..., n_m — количества измерений в сериях;

- соответствующие эмпирические дисперсии.

Оценка (3) обладает теми же свойствами, что и оценка (2), но практически позволяет использовать большее количество информации, что делает ее более надежной.

В частном случае, когда число измерений в каждой серии одно и то же: n_i = n (i=l,...,т), оценка (3) принимает вид

(4)

т. е. здесь в качестве оценки дисперсии принимается среднее арифметическое значение эмпирических дисперсий.

Г. Если для m серий измерений одной и той же величины известны только количества измерений п_х, п_г.................... п_т и средние арифметические результаты х₁, х₂,..., х_т в каждой серии, то в качестве оценки дисперсии применяют эмпирическую дисперсию из средних

= , (5)

где , N = n₁ + n₂ +….+ n_m

Эта оценка является несмещенной и состоятельной (а также асимптотически эффективной при m ).

Д. Для интервального ряда данных (для группированных данных) величина среднего квадрата отклонения s*² является смещенной оценкой дисперсии, причем ее смещение зависит от длины интервала h. Если длина интервала h достаточно мала (составляет не более десятой доли всего диапазона результатов измерений), то в качестве оценки дисперсии применяют исправленную эмпирическую дисперсию

s*² = (6)

Здесь поправка - (поправка Шеппарда) устраняет главную часть смещения, так что оценку (6) можно считать практически несмещенной.

Пример. Для интервального ряда данных, был подсчитан средний квадрат отклонений от среднего значения s*² = 0,05² 6,58. Учитывая поправку Шеппарда - h²/12= = - 0,05²/12 = - 0,05² 0,08, получаем следующее значение исправленной эмпирической дисперсии:

s*² = = 0,05² 6,58

Во всех указанных выше случаях эмпирический стандарт s = - (эмпирическая средняя квадратическая ошибка) дает смещенную (несколько преуменьшенную) оценку средней квадратической ошибки 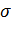. Смещение этой оценки зависит от числа измерений n и уменьшается с увеличением числа п (так, при п = 16 это смещение составляет 2 %, а при n = 26 оно менее 1 %).

Доверительные оценки средней квадратической ошибки. При большом числе измерений доверительную оценку средней квадратической ошибки σ записывают в виде оценки относительного отклонения оцениваемого значения σ от подходящего эмпирического стандарта s (или s_*, S, 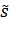,). Такая оценка имеет вид

|(σ - s)/s| < q,

или

s(1 - q) < σ < s(l + q), (7)

 

	А	Б	В	Г	Д
Эмпирический
стандарт	s^*	s	S
Число степеней свободы k	n	n - 1	N— т	m - 1	п — 1

где значение коэффициента q = q( k) находится по (приложение, стр. 175) в зависимости от доверительной вероятности (надежности оценки) и от числа степеней свободы k. Число степеней свободы равно числу обрабатываемых результатов измерений, уменьшенному на число связывающих их линейных соотношений, т. е. оно зависит не только от числа измерений, но и от вида эмпирического стандарта, применяемого для оценки σ. Число степеней свободы определяется по табл. 1.

Здесь N = n₁ + n₂ +….+ n_m число всех измерений в случае В.

Доверительная оценка для случая Д является весьма приближенной и может применяться только при достаточно большом числе n (не менее 50) и достаточно малой длине интервала h (не более 0,5 s*).

Заметим еще, что при достаточно большом числе k можно пользоваться и правилом трех сигм, которое в данном случае имеет вид

,

надежность такой доверительной оценки превосходит

0,99 при k > 47,

0,992 при k > 100,

0,995 при k > 200.

При малом числе измерений симметричная оценка вида (7) приводит к неоправданно большим доверительным интервалам в силу резкой асимметрии распределения эмпирического стандарта (см. рис.).

Поэтому при малом числе измерений применяют асимметричные довери­тельные оценки вида sZ_l < о < sZ₂; значения коэффициентов Z₁ =Z₁ (, k) и Z_г = Z₂ (, k) находятся (приложение, стр. 176) в зависимости от доверительной вероятности

Дата добавления: 2015-08-20