
Читайте также:
|
Сравнение средних при известных дисперсиях. Сравнение средних при неизвестной дисперсии. Проверка гипотезы о равенстве средних значений.
Целью эксперимента нередко бывает выявление различий между значениями определенного параметра в разных объектах исследования. Например, при создания нового материала (или прибора) может быть обнаружено, что значение какого-либо его параметра отличается от значений того же параметра у ранее созданного материала (или прибора), но отличие незначительно; при этом возникает подозрение, не вызвано ли это отличие лишь
случайными ошибками эксперимента. Аналогичный вопрос возникает в промышленности, когда в разных условиях (например, на разном оборудовании или при разной технологии) изготовляются изделия с одними и теми же заданными номинальными значениями какого-либо параметра, а проверка обнаруживает расхождение между средними значениями этих параметров; здесь важно выяснить, имеем ли мы дело с различным качеством изделий или со случайными отклонениями.
Для выяснения вопроса о случайном или неслучайном расхождении значений некоторого параметра х проводят две серии экспериментов (измерений) и для каждой из них подсчитывают среднее значение параметра, скажем, 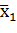 и
и  . Вопрос сводится к тому, когда считать разность между этими средними достаточно большой для того, чтобы иметь практическую уверенность в неслучайном происхождении обнаруженных различий.
. Вопрос сводится к тому, когда считать разность между этими средними достаточно большой для того, чтобы иметь практическую уверенность в неслучайном происхождении обнаруженных различий.
Ниже излагается решение этого вопроса в терминах результатов измерений. Измерения предполагаются независимыми и, по крайней мере, в пределах каждой серии, равноточными; распределение ошибок измерения предполагается нормальным.
Сравнение средних при известных дисперсиях. Пусть произведено n1, независимых равноточных измерений в первой серии и п2 - во второй, причем заранее известны дисперсии ошибок в первой и во второй сериях ( и
и 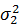 | соответственно). Средние значения результатов измерений в первой и во второй сериях обозначим соответственно через
| соответственно). Средние значения результатов измерений в первой и во второй сериях обозначим соответственно через  и
и  . Для решения вопроса о случайном или неслучайном расхождении этих средних значений подсчитываем отношение
. Для решения вопроса о случайном или неслучайном расхождении этих средних значений подсчитываем отношение
 , (1)
, (1)
Далее задаем желаемую вероятность вывода  и по ней находим (прилож, стр. 172) соответствующее значение t (
и по ней находим (прилож, стр. 172) соответствующее значение t ( (например, при
(например, при  = 0,99 находим t = 2,576).
= 0,99 находим t = 2,576).
Если абсолютная величина отношения (1) превосходит найденное значение t ( ), то расхождение средних значений можно считать неслучайным (значимым) с надежностью вывода
), то расхождение средних значений можно считать неслучайным (значимым) с надежностью вывода  . В противном случае нет оснований считать расхождение значимым (т. е. оно может быть объяснено случайными отклонениями).
. В противном случае нет оснований считать расхождение значимым (т. е. оно может быть объяснено случайными отклонениями).
На практике иногда поступают следующим образом. Подсчитав отношение (1), находят по табл. ближайшее к нему меньшее значение t ( ). Тогда вывод о значимости расхождения средних значений имеет надежность
). Тогда вывод о значимости расхождения средних значений имеет надежность  . Если эта надежность достаточна, то указанный вывод принимается, в противном случае — отбрасывается. Если надежность вывода недостаточна, а сомнение в неслучайности расхождения средних осталось, то может оказаться целесообразным увеличить число измерений в каждой серии для более надежного решения вопроса.
. Если эта надежность достаточна, то указанный вывод принимается, в противном случае — отбрасывается. Если надежность вывода недостаточна, а сомнение в неслучайности расхождения средних осталось, то может оказаться целесообразным увеличить число измерений в каждой серии для более надежного решения вопроса.
Если дисперсии ошибок для обеих серий измерений одинаковы: 
 = σ2, то отношение (1) сводится к
= σ2, то отношение (1) сводится к
 , (2)
, (2)
Сравнение средних при неизвестной дисперсии. Если дисперсии ошибок заранее не известны, то сравнение средних производится только при добавочном предположении, что дисперсии ошибок в обеих сериях измерений одинаковы (это предположение либо принимается без проверки, например, когда две серии измерений производятся одним и тем же прибором, Пусть с одной и той же точностью произведены две серии независимых измерений, причем п1 измерений в первой серии дали среднее значение 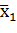 и эмпирическую где
и эмпирическую где  и п2 измерений во второй серии дали соответственно
и п2 измерений во второй серии дали соответственно 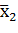 и
и  . Для решения вопроса о случайном или неслучайном расхождении средних значений подсчитываем отношение
. Для решения вопроса о случайном или неслучайном расхождении средних значений подсчитываем отношение
 , (3)
, (3)
где
 , (4)
, (4)
Далее задаем желаемую вероятность вывода  и в (приложение, стр. 174) находим значение t (
и в (приложение, стр. 174) находим значение t ( k), соответствующее заданной вероятности
k), соответствующее заданной вероятности  и числу степеней свободы k = n1 + n2 - 2.
и числу степеней свободы k = n1 + n2 - 2.
Если абсолютная величина отношения (3) превосходит найденное значение t ( ; k), то расхождение средних значений можно считать неслучайным (значимым) с надежностью вывода
; k), то расхождение средних значений можно считать неслучайным (значимым) с надежностью вывода  . В противном случае нет оснований считать расхождение значимым.
. В противном случае нет оснований считать расхождение значимым.
Заметим, что если отношение (3) оказывается лишь немного меньшим значения t ( ; k) при заданной вероятности
; k) при заданной вероятности  , то может быть целесообразным увеличить число измерений для получения более надежного вывода (тем более, что значения t (
, то может быть целесообразным увеличить число измерений для получения более надежного вывода (тем более, что значения t ( k) уменьшаются с увеличением k).
k) уменьшаются с увеличением k).
Величина определяемая по формуле, (4), служит оценкой неизвестной дисперсии s2. Ее можно представить также через средние квадратические отклонения от средних значений
 =
=  ,
, 
А именно
 , (5)
, (5)
Проверка гипотезы о равенстве средних значений. Методы сравнения средних значений можно применять и для решения задачи проверки гипотезы о равенстве средних. Задача эта ставится следующим образом. Имеются две совокупности элементов, различающихся некоторым признаком х. Считается установленным (или проверенным заранее), что распределения признака в обеих совокупностях достаточно хорошо описываются общими нормальными распределениями вероятностей с одинаковой дисперсией σ2 (она может быть и неизвестной). Проверяется гипотеза о равенстве центров этих нормальных распределений (что вместе с уже принятыми предположениями означает теперь полное совпадение законов распределения). Проверяемая гипотеза обычно называется нуль-гипотезой. Для ее проверки из каждой совокупности берут случайную выборку, т. е. случайным образом (как в лотерее) отбирают некоторое количество элементов. Пусть количество отобранных элементов (объем, выборки) из первой совокупности есть n1 а из второй — n2. Подсчитываем средние значения признака в каждой выборке, пусть эти средние равны  и
и  . Если дисперсия σ2 неизвестна, то подсчитываем еще и эмпирические дисперсии
. Если дисперсия σ2 неизвестна, то подсчитываем еще и эмпирические дисперсии  и
и  .
.
В предположении, что нуль-гипотеза верна, отношения (2) и (3) представляют собой случайные величины с вполне определенными законами распределения. Поэтому, задавая желаемую вероятность вывода  (например 0,99), мы можем найти симметричный интервал (-
(например 0,99), мы можем найти симметричный интервал (-  ), вероятность попадания в который равна
), вероятность попадания в который равна 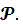 Другими словами, при справедливости всех высказанных выше предположений и нуль-гипотезы отношение (2) или (3) может попасть в интервал(-
Другими словами, при справедливости всех высказанных выше предположений и нуль-гипотезы отношение (2) или (3) может попасть в интервал(-  ) случайно с вероятностью
) случайно с вероятностью  Точки, лежащие вне этого интервала, образуют критическую область (заштрихованную на рис.),
Точки, лежащие вне этого интервала, образуют критическую область (заштрихованную на рис.),

вероятность попадания в которую составляет 1 -  . Значения
. Значения 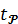 = t(
= t( (при известной дисперсии) или
(при известной дисперсии) или 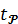 = t(
= t( (при неизвестной дисперсии), определяющие границы указанной доверительной области, называются критическими; именно эти значения приведены в (приложение, стр. 172 и 174).
(при неизвестной дисперсии), определяющие границы указанной доверительной области, называются критическими; именно эти значения приведены в (приложение, стр. 172 и 174).
Если отношение (2) или (3), подсчитанное по значениям признака в выборках, попадет в критическую область (т. е. если абсолютная величина соответствующего отношения превзойдет критическое значение из табл. II или табл. IV), то нуль-гипотезу отвергают с надежностью  , т. е. считают, что результаты эксперимента противоречат нуль-гипотезе. В противном случае нуль-гипотезу принимают, т. е. считают, что результаты эксперимента не противоречат нуль-гипотезе (но, разумеется, не могут служить и доказательством этой гипотезы).
, т. е. считают, что результаты эксперимента противоречат нуль-гипотезе. В противном случае нуль-гипотезу принимают, т. е. считают, что результаты эксперимента не противоречат нуль-гипотезе (но, разумеется, не могут служить и доказательством этой гипотезы).
Заметим, что мы выбрали симметричный интервал (-  ) и, значит, симметричную критическую область в связи с симметрией распределения отношений (2) и (3) относительно нуля. Возможен выбор и несимметричных критических областей, например, в задачах, где проверяемая гипотеза a1 = a2 конкурирует с гипотезой а1 > а2 (а1 и а2 - центры соответствующих распределений).
) и, значит, симметричную критическую область в связи с симметрией распределения отношений (2) и (3) относительно нуля. Возможен выбор и несимметричных критических областей, например, в задачах, где проверяемая гипотеза a1 = a2 конкурирует с гипотезой а1 > а2 (а1 и а2 - центры соответствующих распределений).
Дата добавления: 2015-08-20; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оценки истинного значения измеряемой величины. | | | Точечные оценки дисперсии. |