Сравнение дисперсий.

Сравнение двух дисперсий. Выделение большей дисперсии из многих.

При выполнении измерений в различных условиях возникает задача сравнения точности измерений. В частности, возникает задача сравнения точности различных измерительных приборов. Важность этой задачи особенно подчеркивается тем обстоятельством, что доверительные интервалы для средних квадратических ошибок оказываются обычно весьма широкими. Отметим также, что и в задачах сравнения средних иногда приходится сначала проверять равенство дисперсий.

Сравнение двух дисперсий. Пусть по результатам двух рядов измерений получены эмпирические дисперсии:

при числе степеней свободы k₁

при числе степеней свободы k₂

Будем считать, что индекс 1 относится к большей эмпирической дисперсии.

Для решения вопроса о случайном или неслучайном расхождений дисперсий рассматривают отношение большей эмпирической дисперсии к меньшей

/ = F > l. (1)

Затем задают желаемую надежность вывода = 0,95 или = 0,99 по (прилож. стр. 177) находят критическое значение отношения F, соответствующее данным числам степеней свободы и k₁ и k₂ (напомним, что число степеней свободы k_t относится к большей эмпирической дисперсии).

Если отношение (1), подсчитанное по результатам измерений, оказывается больше критического значения, то расхождение дисперсий считают неслучайным (значимым) с надежностью . Другими словами, в этом случае точность измерений существенно различна для двух рядов измерений. В противном случае для такого утверждения нет достаточных оснований.

Точно так же поступают при проверке гипотезы о равенстве дисперсий. Если отношение (1), подсчитанное для двух выборок, оказывается больше критического значения, то гипотезу о равенстве дисперсий отвергают, в противном случае - принимают.

Пример. Пусть старый измерительный прибор, на котором произведено 200 измерений, имеет точность, определяемую эмпирической дисперсией 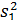= 3,82 (кв. единиц). Новый измерительный прибор при первых пятнадцати измерениях дал эмпирическую дисперсию = 2,00 (кв. единиц). Можно ли считать, что новый прибор дает существенно лучшую точность, чем старый?

Решение. Сравнение дисперсий по формуле (1) дает 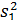/ = F = 1,91, причем числа степеней свободы соответственно равны

h₁ = 200-1 = 199 и h₂=15 - 1 = 14.

Так как полученное здесь отношение меньше критического даже при надежности 0,95 (что по табл. VII составляет более 2,13), те приведенные данные не дают оснований считать точность нового прибора лучшей, чем точность старого.

Для окончательного решения вопроса надо произвести большее число измерений новым прибором. Если, например, при трех сериях по пятнадцати измерений среднее значение дисперсии останется тем же, = 2,00, то, учитывая увеличение числа степеней свободы до k₂ = 3 14 = 42, мы найдем, что с надежностью 0,99 дисперсия нового прибора существенно меньше дисперсии старого, т. е. точность нового прибора выше.

Выделение большей дисперсии из многих. Пусть среди нескольких приборов (нескольких серий измерений) обнаружен прибор (серия измерений), эмпирическая дисперсия которого заметно больше остальных. Задача заключается в том, чтобы выяснить, можно ли считать отличие выделенной дисперсии от остальных случайным или это отличие следует считать существенным (значимым). Для решения задачи поступают следующим образом, Производят каждым из m испытуемых приборов одинаковое число n измерений, подсчитывают эмпирические дисперсии , … 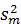( > ) при i > 1и сравнивают наибольшую дисперсию с суммой всех дисперсий по формуле

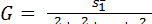, (2)

Если отношение (2) оказывается больше критического значения, приведенного в (прилож, стр. 178), то отличие первой дисперсии от остальных считается существенным, т. е. считают первый прибор (первую серию измерений) менее точным, чем остальные. В противном случае для такого утверждения нет достаточных оснований.

В табл. критические значения отношения G приведены для двух доверительных вероятностей = 0,95 и = 0,99 и для различных сочетаний чисел m (числа приборов, серий измерений) и k =n -1 (числа степеней свободы).

Пример. Пусть на шести приборах произведено по семи измерений, которые дали эмпирические дисперсии

3,82; 1,70; 1,30; 0,92; 0,78 и 0,81.

Сравнивая первую дисперсию с суммой всех дисперсий, вычисляем отношение (2): G = 0.41

Это отношение оказывается меньше критического значения при т = 6 и k = n - 1 = 6 даже для доверительной вероятности 0,95 (таблица дает критическое значение 0,418). Поэтому нет оснований считать дисперсию 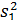= 3,82 существенно больше остальных. Заметим, что если бы такие же данные встретились при n = 11 измерениях, то с надежностью, большей 0,99, можно было бы считать первую дисперсию существенно больше остальных (соответствующее критическое значение при n =10 и = 0,99 составляет 0,408).

Описанный выше критерий применяется также и для проверки однородности ряда дисперсий, т. е. для проверки того, что все эмпирические дисперсии , … относятся к выборкам из совокупностей с одной и той же теоретической дисперсией σ². Если отношение (2) оказывается больше критического значения, то надо считать, что гипотеза об однородности ряда дисперсий не согласуется с эмпирическими данными,

Дата добавления: 2015-08-20