Оценки истинного значения измеряемой величины.

Типы оценок и их свойства. Точечные оценки. Доверительные оценки при равноточных измерениях. Доверительные оценки при неравноточных измерениях. Необходимое количество измерений.

Оценка. Целью статистической оценки является отыскание оценки параметра генеральной совокупности на основе выборочной статистики, взятой из этой совокупности. Обычно требуются два типа оценок: точечные оценки и интервальные оценки.

Точечная оценка — это численное значение статистики, используемое для оценки параметра распределения генеральной совокупности. Например, выборочное среднее x — точечная оценка математического ожидания генеральной совокупности μ. Обычно предполагается, что точечные оценки имеют определенные свойства.

Оценки должны удовлетворять следующим требованиям:

- оценка должна быть состоятельной, т. е. с увеличением объема выборки она должна сходиться к оцениваемому параметру по вероятности;

- оценка должна быть эффективной, т. е. при данном объеме выборки иметь минимальную дисперсию.

- оценка должна быть несмещенной, т. е. математическое ожидание оценки должно равняться оцениваемому параметру.

Общий метод нахождения оценок с нужными свойствами это метод максимума правдоподобия. Практическое значение имеют следующие выборочные характеристики, которые удовлетворяют вышеперечисленным требованиям:

1) в качестве оценки математического ожидания – среднее арифметическое выборки:

, (1)

2) в качестве оценки дисперсии случайной величины х - значение, определяемое формулой:

(2)

3) в качестве оценки дисперсии среднего арифметического x - значение, определяемое формулой:

, (3)

Точечные оценки. Если все n измерений величины а произведены с одинаковой точностью (равноточные измерения), то в качестве оценки истинного значения а измеряемой величины применяют среднее арифметическое значение результатов измерений:

, (4)

Эта оценка является несмещенной и состоятельной. При дополнительном предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей, эта оценка является эффективной.

Если измерения не являются равноточными, но известны веса измерений, т.е. числа p₁, p₂, ….p_n, обратно пропорциональные дисперсиям ошибок σ₁, σ₂ …. σ_n:

p_1: p_2: …:p_n = : :……

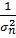
то в качестве оценки истинного значения a измеряемой величины применяют взвешенное среднее арифметическое значение:

, (5)

Эта оценка обладает теми же свойствами, что и оценка (4). Полезно обратить внимание на то, что взвешенное среднее арифметическое значение (5) зависит не от самих весов p₁ p₂..р_п, а только от их отношений.

Например, часто обрабатываемые результаты x_l x₂, х_п представляют собой не результаты непосредственных измерений, асредние в п сериях измерений, произведенных с одной и той же точностью (т. е. с одинаковой средней квадратической ошибкой σ), но при разных количествах измерений в каждой серии. В этом случае каждому значению х_i можно приписать в качестве веса количество измерений в соответствующей серии:

p_i = m_i (i=1, 2, п),

где т_i — количество измерений в серии со средним значением x_i. Это связано с тем, что при указанных условиях дисперсий средних значений x_t обратно пропорциональны количествам измерений т_i в соответствующих сериях:

и, значит,

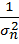: :…… = m₁: m₂:....m_n

Среднее арифметическое значение для интервального ряда данных является смещенной оценкой для а. Величина смещения имеет порядок h², если длина интервала h достаточно мала (в 2—3 раза меньше, чем σ).

Доверительные оценки при равноточных: измерениях. Приводимые ниже доверительные оценки истинного значения а измеряемой величины даются в предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей, Здесь рассматриваются только симметричные доверительные оценки, которые имеют вид неравенств

или

|а - | < ε (6)

где - среднее арифметическое значение (4).

Величина ε определяется по заданной доверительной вероятности (надежности оценки) ; обычно надежность задается в виде одного из трех уровней 0,95, 0,99 или 0,999.

Доверительная оценка при известной точности измерений.

Если заранее известна средняя квадратическая ошибка а (или другая связанная с ней характеристика точности измерений), то доверительная оценка (6) имеет вид

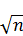|а—х| < t()σ/ , (7)

где п — число измерений, а значение t = t() определяется по заданной доверительной вероятности < из условия

2Ф (t) = (8)

т. е. находится по (прилож. стр. 172).

Таким образом, здесь

t ()

Пример 1. Пусть для десяти измерений, результаты которых приведены в примере (предыдущей лекции), известно, что σ = 0,28; требуется оценить истинное значение измеряемой величины а с надежностью = 0,99.

Решение. По (прилож. С. 172) для = 2Ф (t) = 0,99, т. е. для 1 - = 0,01, находим t = 2,576. Подсчитанное среднее значение результатов измерения равно = 36,06. Следовательно, с надежностью 0,99 можно считать, что

= 0.23

т. е. что значение а лежит в интервале (35,83; 36,29)

Доверительная оценка при неизвестной точности измерений. Если средняя квадратическаи ошибка σ заранее неизвестна, то вместо нее используют эмпирический стандарт

который служит оценкой параметра σ. При этом доверительная оценка (6) принимает вид

|а - | < t() (9)

где множитель t () зависит уже не только от доверительной вероятности , но и от числа измерений n (k = n - 1). Значения этого множителя для пяти уровней надежности и для различных значений числа приведены в (прилож, стр. 174). Таблица составлена с помощью так называемого распределения Стьюдента, т. е. распределения вероятностей отношения : значения t = t() определены так, что

Распределение Стьюдента зависит от одного параметра k, который называется числом степеней свободы; для рассматриваемой задачи число степеней свободы k связано с числом измерений п соотношением k = n - 1.

Пример 2. Пусть для десяти измерений, результаты которых приведены в примере (тот же самый), величина σ не известна. Требуется оценить истинное значение измеряемой величины а с надежностью = 0,99.

Решение. Для результатов измерений среднее значение и среднее квадратическое отклонение подсчитаны и составляют соответственно х = 36,06 и s* = 0,25. По заданной надежности = 0,99 и числу измерений n = 10 находим по табл. IV множитель t (0,99; 9) = 3,250 и получаем доверительную оценку истинного значения а в виде

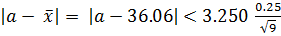= 0,27

таким образом, с надежностью 0,99 можно считать, что значение а заключено в интервале (З5,79; 36,33).

Правило трех сигм. Так как выбор надежности доверительной опенки допускает некоторый произвол, в практике обработки результатов эксперимента широкое распространение получило правило трех сигм;

Отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит, утроенной средней квадратической ошибки этого среднего значения.

Таким образом, правило трех сигм представляет собой доверительную оценку

|а—х | < 3σ/

в случае известной величины σ или доверительную оценку |а—х| < 3s/ в случае неизвестной величины σ.

Необходимое количество измерений. Увеличивая количество измерений n даже при неизменной их точности, можно увеличить надежность доверительных оценок (7) и (9) или сузить доверительный интервал для истинного значения измеряемой величины. Необходимое количество измерений для достижения требуемой точности е и требуемой надежности можно определить заранее только в том случае, когда известна средняя квадратическая ошибка измерений (измерения предполагаются равноточными и независимыми). В этом случае количество измерений для получения доверительной оценки точности ε:

|а - | < ε, с заданной надежностью определяется с помощью формулы (7), откуда

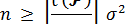
где t = t () находится из равенства 2Ф(t)*= по (прилож/, стр. 172)/

Если средняя квадратическая ошибка измерений заранее неизвестна, но известен хотя бы ее порядок, то необходимое количество измерений можно определить в зависимости от надежности () и от отношения q = ε/s, где s будущий эмпирический стандарт ошибки. Для определения количества п в зависимости от t () и q применяется табл. 2.

Таблица 2

()/ q	0,90	0,95	0,98	0,99	0,999
1,0
0,5
0,4
0,3
0,2
0,1
0,05

Например, чтобы гарантировать получение доверительной оценки с надежностью = 0,99 и точностью до 0,1s, надо произвести 688 измерений. На практике часто можно ограничиться меньшим числом измерений, если применить следующий прием. Сначала нужно произвести Сравнительно небольшое количество измерений (в 3 - 4 раза меньше указанного в таблице). По результатам этих измерений рассчитать доверительный интервал. Затем уточнить необходимое количество измерений из тех соображений, что уменьшение доверительного интервала в 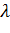раз обеспечивается увеличением количества измерений в раз (например, уменьшение доверительного интервала в 2 раза обеспечивается увеличением количества измерений в 4 раза).

Пример. Приведенная доверительная оценка истинного значения а некоторой величины по результатам n = 10 ее измерений дала точность 0,27 с надежностью 0,99. Если при той же надежности мы хотим оценить а с точностью до 0,1, т. е. уменьшить доверительный интервал в 2,7 раза, то мы должны довести число измерений до 10 (2,7)² = 73 (на самом деле немного меньше, так как при этом и t (0,99; k) уменьшится с 3,25 до 2,65).

Заметим, что больший эффект дает увеличение точности отдельных измерений

---

Дата добавления: 2015-08-20