Лекция 10.

Основные понятия планирования эксперимента.

Мысль о том, что эксперимент можно планировать, восходит к глубокой древности. Наш далекий предок, убедившийся, что острым камнем можно убить даже мамонта, несомненно выдвигал гипотезы, которые после целенаправленной экспериментальной проверки привели к созданию копья, дротика, а затем и лука со стрелами.

Он, однако, не пользовался статистическими методами, поэтому остается непонятным, как он вообще выжил и обеспечил тем самым наше существование.

Только в начале нашего века люди, наконец, поняли, что дальше дело так не пойдет, и придумали статистические методы планирования эксперимента. Честь открытия этой идеи принадлежит английскому статистику Рональду Фишеру (конец двадцатых годов), который впервые показал целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному эксперименту. Понадобилось еще несколько десятилетий, чтобы в начале пятидесятых годов появилось новое направление в планировании эксперимента, связанное с оптимизацией процессов, – планирование экстремального эксперимента. Первая работа в этой области была опубликована в 1951 г. Боксом и Уилсоном в Англии. Идея метода Бокса–Уилсона крайне проста. Экспериментатору предлагается ставить последовательные небольшие серии опытов, в каждой из которых одновременно варьируются по определенным правилам все факторы. Серии организуются таким образом, чтобы после математической обработки предыдущей можно было выбрать условия проведения (т.е. спланировать) следующую серию. Так последовательно, шаг за шагом, достигается область оптимума.

Применение планирования эксперимента делает поведение экспериментатора целенаправленным и организованным, существенно способствует повышению производительности его труда и надежности полученных результатов. Важным достоинством метода является его универсальность, пригодность в огромном большинстве областей исследования, интересующих современного человека. В нашей стране планирование эксперимента развивается с 1960 г. под руководством В. В. Налимова.

Интерес исследователей к планированию эксперимента вполне понятен: перспектива сократить число опытов, найти оптимум, получить количественные оценки влияния факторов и определить ошибки – крайне привлекательна.

Но, когда экспериментатор делает попытку познакомиться с планированием эксперимента, он часто сталкивается с серьезными трудностями. Больше того, иногда он просто неверно применяет методы планирования или выбирает не самый оптимальный для данной ситуации путь исследования, или допускает еще какие–нибудь досадные ошибки. При этом снижается эффективность его работы и появляется опасность дискредитации важного и полезного направления.

Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и участках, в клиниках и т.д. Эксперимент может быть физическим, психологическим или модельным. Он может непосредственно проводиться на объекте или на его модели. Модель обычно отличается от объекта масштабом, а иногда природой.

Как вы считаете, можно ли поставить эксперимент на абстрактной математической модели?

Если модель достаточно точно описывает объект, то эксперимент на объекте может быть заменен экспериментом на модели. В последнее время наряду с физическими моделями все большее распространение получают абстрактные математические модели. Можно получать новые сведения об объекте, экспериментируя на модели, если она достаточно точно описывает объект.

Эксперимент занимает центральное место в науке. Однако возникает вопрос, насколько эффективно он используется. Джон Бернал, например, отмечал, что научные исследования организуются и проводятся настолько хаотично, что их коэффициент полезного действия может быть оценен величиной порядка 2 %. Для того чтобы повысить эффективность исследований, требуется нечто совершенно новое. Одним из возможных путей является применение математических методов, построение математической теории планирования эксперимента.

Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом существенно следующее:

- стремление к минимизации общего числа опытов;

- одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам – алгоритмам;

- использование математического аппарата, формализующего многие действия экспериментатора;

- выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.

Задачи, для решения которых может использоваться планирование эксперимента, чрезвычайно разнообразны.

Поиск оптимальных условий, построение интерполяционных формул, выбор существенных факторов, оценка и уточнение констант теоретических моделей (например, кинетических), выбор наиболее приемлемых из некоторого множества гипотез о механизме явлений, исследование диаграмм состав–свойство – вот примеры задач, при решении которых применяется планирование эксперимента. Можно сказать, что там, где есть эксперимент, имеет место и наука о его проведении – планирование эксперимента.

Поиск оптимальных условий является одной из наиболее распространенных научно–технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие (оптимальные в некотором смысле) условия его реализации.

Пусть, например, у химика возникла гипотеза о том, что при взаимодействии двух веществ должен получаться некоторый интересующий его продукт. Чтобы убедиться в правильности своей гипотезы, он начинает проводить эксперимент. Возможно, что ему повезло и он получил требуемый продукт. Однако выход продукта весьма низок, скажем, 2 %. Вот тут–то и возникает задача выбора оптимальных условий. Требуется так подобрать концентрации реагирующих веществ, температуру, давление, время реакции и другие факторы, чтобы сделать выход возможно более близким к 100 %. В данном примере находятся условия проведения процесса, оптимальные в смысле максимизации выхода требуемого продукта. Но это далеко не единственно возможная постановка задачи. Найденные условия оказались бы другими, если бы ставилась, например, цель минимизации себестоимости продукта или минимизации количества вредных примесей. Следует подчеркнуть, что всегда необходимо четко формулировать, в каком смысле условия должны быть оптимальными. Этим определяется выбор цели исследования. Точная формулировка цели в значительной мере определяет успех исследования.

Задачи, сформулированные аналогичным образом, называются задачами оптимизации. Процесс их решения называется процессом оптимизации или просто оптимизацией. Выбор оптимального состава многокомпонентных смесей или сплавов, повышение производительности действующих установок, повышение качества продукции, снижение затрат на ее получение – вот примеры задач оптимизации.

Эксперимент, который ставится для решения задач оптимизации, называется экстремальным. Это название связано с глубокой аналогией между оптимизацией и поиском экстремума некоторой функции. Давайте рассмотрим следующие две задачи.

1. Прочность бетона в значительной степени определяется маркой цемента, количеством наполнителя и количеством воды. Требуется установить связь между прочностью бетона и названными факторами.

2. Надежность некоторого полупроводникового прибора зависит от ряда технологических факторов. Требуется так подобрать значения этих факторов, чтобы надежность прибора повысилась.

Как вы думаете, какая из этих задач является экстремальной?

Чтобы облегчить вам выбор, укажем на признак, отличающий экстремальные задачи. Задача является экстремальной, если цель ее состоит в поиске экстремума некоторой функции. Чтобы установить, какая из двух задач является экстремальной, надо обратиться к их формулировкам и выяснить, где удовлетворяются требования экстремальности. В задаче 1 требуется установить связь между прочностью бетона и тремя факторами. Здесь не определено, какая прочность является оптимальной, и не требуется ее оптимизировать. В задаче 2 необходимо повысить надежность прибора. Сама постановка задачи указывает на то, что существующая надежность не удовлетворяет экспериментатора и требуется поиск таких условий, при которых ее значения повысятся. Задачи называем интерполяционными, а типа 2 – экстремальными.

Чтобы продвинуться дальше, нам придется определить еще ряд важных понятий, первое из которых – «объект исследования». Для описания объекта исследования удобно пользоваться представлением о кибернетической системе, которая схематически изображена на рисунке. Иногда такую кибернетическую систему называют «черным ящиком». Стрелки справа изображают численные характеристики целей исследования. Мы обозначаем их буквой игрек и называем параметрами оптимизации В литературе вы можете встретить другие названия: критерий оптимизации, целевая функция, выход «черного ящика» и т.д.

Для проведения эксперимента необходимо иметь возможность воздействовать на поведение «черного ящика». Все способы такого воздействия мы обозначаем буквой икс и называем факторами. Их называют также входами «черного ящика».

При решении задачи будем использовать математические модели объекта исследования. Под математической моделью мы понимаем уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде можно записать так:

y=j(x₁, x₂, x₃,…, x_n)

где символ j (), как обычно в математике, заменяет слова: «функция от». Такая функция называется функцией отклика.

Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Может оказаться, что фактор способен принимать бесконечно много значений (непрерывный ряд). Однако на практике точность, с которой устанавливается некоторое значение, не беспредельна. Поэтому мы вправе считать, что всякий фактор имеет определенное число дискретных уровней. Это соглашение существенно облегчает построение «черного ящика» и эксперимента, а также упрощает оценку их сложности.

Фиксированный набор уровней факторов (т.е. установление каждого фактора на некоторый уровень) определяет одно из возможных состояний «черного ящика». Одновременно это есть условия проведения одного из возможных опытов. Если перебрать все возможные наборы состояний, то мы получим полное множество различных состояний данного «ящика». Одновременно это будет число возможных различных опытов.

Чтобы узнать число различных состояний, достаточно число уровней факторов (если оно для всех факторов одинаково) возвести в степень числа факторов k: p^k, где р – число уровней.

Yа первый взгляд простая система с пятью факторами на пяти уровнях имеет 3125 состояний, а для десяти факторов на четырех уровнях их уже свыше миллиона!

В этих условиях мы просто вынуждены отказаться от таких экспериментов, которые включают все возможные опыты: перебор слишком велик. Тогда возникает вопрос: сколько и каких опытов надо включить в эксперимент, чтобы решить поставленную задачу? Здесь–то и приходит на помощь планирование эксперимента.

Однако нужно иметь в виду, что при планировании эксперимента не безразлично, какими свойствами обладает объект исследования. Укажем два основных требования, с которыми приходится считаться. Прежде всего существенно, воспроизводятся ли на объекте результаты эксперимента. Выберем некоторые уровни для всех факторов и в этих условиях проведем эксперимент. Затем повторим его несколько раз через неравные промежутки времени и сравним значения параметра оптимизации. Разброс этих значений характеризует воспроизводимость результатов. Если он не превышает некоторой заранее заданной величины (наших требований к точности эксперимента), то объект удовлетворяет требованию воспроизводимости результатов, а если превышает, то не удовлетворяет этому требованию. Мы будем рассматривать только такие объекты, для которых требование воспроизводимости выполняется.

Планирование эксперимента предполагает активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые представляют интерес. Поэтому такой эксперимент называется активным. Объект, на котором возможен активный эксперимент, называется управляемым. Это и есть второе требование к объекту исследования.

На практике нет абсолютно управляемых объектов. На реальный объект обычно действуют как управляемые, так и неуправляемые факторы. Неуправляемые факторы влияют на воспроизводимость эксперимента и являются причиной ее нарушения. Если требования воспроизводимости не выполняются, приходится обращаться к активно–пассивному эксперименту.

Возможно, плохая воспроизводимость объясняется действием фактора, систематически изменяющегося (дрейфующего) во времени. Тогда нужно обращаться к специальным методам планирования. Наконец, возможно, что все факторы неуправляемы. В этом случае возникает задача установления связи между параметром оптимизации и факторами по результатам наблюдений за поведением объекта, или, как говорят, по результатам пассивного эксперимента.

Планирование экстремального эксперимента – это метод выбора количества и условий проведения опытов, минимально необходимых для отыскания оптимальных условий, т. е. для решения поставленной задачи.

Понятие «объект исследования» требует точного формального определения. Для такого определения удалось приспособить кибернетическое понятие «черный ящик» – модель объекта. Экспериментатор, вставший на путь применения методов планирования эксперимента, должен уметь формулировать свою задачу в терминах «черного ящика».

Входы «черного ящика» называются факторами. Каждый фактор может принимать некоторое определенное число различных значений, называемых уровнями. Сочетание определенных уровней всех факторов определяет возможное состояние «черного ящика» и условия одного из возможных опытов.

Совокупность всех различных возможных состояний определяет сложность «черного ящика» и общее число возможных опытов.

Результаты эксперимента используются для получения математической модели объект исследования, которая представляет собой уравнение, связывающее параметр оптимизации и факторы. Такое уравнение называется функцией отклика.

Использование для получения модели всех возможных опытов приводит к абсурдно, большим экспериментам. Задача выбора необходимых для эксперимента опытов, методов математической обработки их результатов и принятия решений – это и есть задача планирования эксперимента. Частный случай этой задачи – планирование экстремального эксперимента, т. е. эксперимента, поставленного с целью поиска оптимальных условий функционирования объекта. Планирование экстремального эксперимента – метод выбора минимального количества опытов, необходимых для отыскания оптимальных условий.

Под экспериментом будем понимать метод научного исследования, когда исследователь активно и целенаправленно воздействует на объект исследования путем создания искусственных условий или использования естественных с целью получения информации о его свойствах.

Важнейшей задачей методов обработки полученной в ходе эксперимента информации является задача построения математической модели изучаемого явления, процесса, объекта. Ее можно использовать и при анализе процессов и при проектировании объектов. Другой задачей обработки полученной в ходе эксперимента информации является задача оптимизации, т.е. нахождения такой комбинации влияющих независимых переменных, при которой выбранный показатель оптимальности принимает экстремальное значение.

Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления.

Под планом эксперимента – понимается совокупность данных, определяющих число, условия и порядок реализации опытов. Под словом опыт в данном случае имеется в виду отдельная, элементарная часть эксперимента. Соответственно, понятие планирование эксперимента, определяемое как процесс разработки плана эксперимента, включает в себя все, что делается по разработке стратегии экспериментирования от начальных до заключительных этапов изучения объекта исследования, т.е. от получения априорной информации до создания работоспособной математической модели объекта исследования или определения оптимальных условий. Планирование способствует значительной интенсификации труда исследователя и сокращению затрат на эксперимент, повышению достоверности полученных результатов исследования.

Основным математическим аппаратом теории планирования эксперимента является теория вероятностей и математическая статистика.

Многомерное факторное пространство – это множество точек, каждая из которых соответствует определенной комбинации факторов. Область возможных комбинаций факторов называется областью возможных (допустимых) планов эксперимента.

Вектор, образуемый выходными параметрами–характеристиками свойств или качеств объекта, называют откликом, а зависимость отклика от рассматриваемых факторов – функцией отклика. Геометрическое представление функции отклика в факторном пространстве называют поверхностью отклика. Функцию отклика называют также целевой функцией, имея в виду, что при планировании эксперимента с целью нахождения оптимальных условий она является критерием оптимальности.

Планирование эксперимента проводится в несколько этапов:

- постановка задачи (определение цели эксперимента, выяснение исходной ситуации, оценка допустимых затрат времени и средств, установление типа задачи);

- сбор априорной информации (получение литературы, опрос специалистов и т.п.);

- выбор способа решения и стратегии его реализации (установление типа модели, выявление возможных влияющих факторов, выявление выходных параметров, выбор целевых функций, создание необходимых нестандартных технических средств, формулировка статистических задач, выбор или разработка алгоритмов программ обработки экспериментальных данных).

Основными концепциями современного подхода к организации эксперимента являются рандомизация, многофакторность и автоматизация.

Сущность рандомизации состоит в следующем. Любое экспериментальное исследование проводится, как правило, в условиях действия систематических ошибок и факторов, которые трудно поддаются учету и контролю. При традиционном подходе к эксперименту исследователи нередко пытаются отделить изучаемое явление от мешающих факторов, как это можно сделать в детерминированных объектах с хорошо изученной структурой. Очевидно, что в недетерминированных объектах с огромным количеством случайных факторов ценность эксперимента, проведенного в особых условиях, не может быть высокой.

Концепция рандомизации предлагает принципиально новый подход к организации выборочных данных эксперимента. План эксперимента составляется таким образом, чтобы рандомизировать, то есть сделать случайными в пространстве и во времени, систематически действующие мешающие факторы. Тогда эти факторы можно рассматривать как случайные величины и, следовательно, учесть статистически их влияние в значении ошибки эксперимента. Иными словами, в противоположность традиционному подходу к эксперименту со стремлением стабилизировать мешающие факторы рандомизация внесла концепцию случая в эксперимент.

Принцип многофакторности отражает новый подход к эксперименту в задачах с многими факторами. При изучении объектов с несколькими факторами согласно этому принципу исследователю предлагается ставить опыты так, чтобы варьировать все факторы сразу в отличие от традиционного подхода, когда исследователь пытается изучать действие каждого фактора при поочередном варьировании. Организация эксперимента с применением многофакторных схем варьирования позволяет повысить точностью оценок параметров подбираемых моделей для недетерминированных объектов, точнее оценить чувствительность выходной зависимой переменной объекта к вариации изучаемых входных независимых переменных.

Развитие технических программных средств вычислительной техники дает возможность говорить о новой концепции в организации научных исследований – автоматизации эксперимента. Технические средства вычислительных комплексов позволяют на качественно новом уровне по точности, быстродействию и наглядности решать задачи сбора, переработки и отображения информации. Программные средства предоставляют исследователю новые возможности организации процесса анализа данных, создания автоматически управляемой последовательности процедур анализа, использования интерактивного режима работы с пакетами прикладных программ.

Среди основных методов планирования, применяемых на разных этапах исследования, используют:

- планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению;

- планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами;

- планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и иные);

- планирование экстремального эксперимента, в котором главная задача – экспериментальная оптимизация объекта исследования;

- планирование при изучении динамических процессов и т.д.

При пассивном эксперименте существуют только факторы в виде входных контролируемых, но неуправляемых переменных, и экспериментатор находится в положении пассивного наблюдателя. Задача планирования в этом случае сводится к оптимальной организации сбора информации и решению таких вопросов, как выбор количества и частоты измерений, выбор метода обработки результатов измерений.

Наиболее часто целью пассивного эксперимента является построение математической модели объекта, которая может рассматриваться либо как хорошо, либо как плохо организованный объект. В хорошо организованном объекте имеют место определенные процессы, в которых взаимосвязи входных и выходных параметров устанавливаются в виде детерминированных функций. Поэтому такие объекты называют детерминированными. Плохо организованные или диффузные объекты представляют собой статистические модели. Методы исследования с использованием таких моделей не требуют детального изучения механизма процессов и явлений, протекающих в объекте.

Однофакторный пассивный эксперимент проводится путем выполнения n пар измерений в дискретные моменты времени единственного входного параметра х и соответствующих значений выходного параметра y. Аналитическая зависимость между этими параметрами вследствие случайного характера возмущающих воздействий рассматривается в виде зависимости математического ожидания y от значения х, носящей название регрессионной. Соответствующая линия А В показана на графике (рис.1).

Рис 9.1. График регрессионной зависимости y от х

Множество всех точек проведения экспериментов x ⁱ =(x ⁱ ₁, x ⁱ ₂, …, x ⁱ _n), i = 1, 2, …. N представляется с помощью матрицы

и называется планом эксперимента

Целью однофакторного пассивного эксперимента является построение регрессионной модели. Следует отметить, что регрессионная модель является приближенной оценкой истинной регрессионной зависимости. Для построения модели следует провести обоснованный выбор аппроксимирующей функции. Критериями выбора являются простота, удобство пользования, обеспечение требуемой точности аппроксимации, адекватность. Адекватная регрессионная модель позволяет предсказывать с требуемой точностью значения выходной величины в некоторой области значений входной.

Нередко для выбора аппроксимирующей функции пользуются кривой регрессионной зависимости, проведенной "на глаз".

Чаще всего регрессионная модель представляется с помощью аппроксимирующей функцией в виде полинома

. (2)

Приняв такую модель, следует определиться в порядке полинома, после чего вычислить параметры а₁, а₂,…,а_m.

В общем случае результаты измерения l_i значения выходной величины и ее значения y_i определяемые регрессионной зависимостью от входного фактора x_i, не совпадают, т.е. отлична от нуля разность D_i = l_i–y_i, что связано с наличием погрешности измерения и возмущающих воздействий. Обычно считают, что D_i не зависит от значения y (т.е. аддитивна) и подчиняется нормальному закону распределения с нулевым математическим ожиданием.

Если выполнено n измерений, то их результаты можно записать в виде:

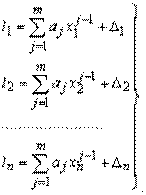(3)

Система уравнений (3) линейна относительно a_j. Для нахождения оценок a_j из условия минимума D_j необходимо добиться равенства нулю всех частных производных функций по a_j. Получим систему нормальных уравнений:

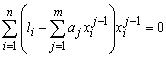(j=1,2,…,m). (4)

Сгруппировав все коэффициенты при неизвестных a_j и записав уравнения системы (4) в стандартном виде можно вычислить искомые параметры a_j методом определителей.

Многофакторный пассивный эксперимент дает n значений выходного параметра y объекта, соответствующих измерениям n совокупностей значений выходных параметров:

x₁₁, x₁₂,…, x_1k;

x₂₁, x₂₂,…, x_2k;

.……...............

x_n1, x_n2,…, x_nk.,

где x_ij – значение j входного параметра в i–м измерении (j=1,2,...,n).

В качестве регрессионной модели примем линейный многочлен вида

у = а₀ + а₁х₁ +a₂x₂+ …+ а_kх_k. (5)

Заменим переменные их центрированными значениями:

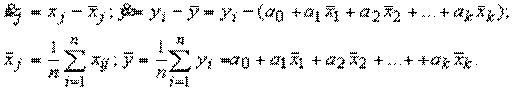
Тогда модель принимает вид

, (6)

На основе (6) составляется система нормальных уравнений вида (4) (с заменой m на k) и вычисляются оценки параметров . Затем вычисляется оценка

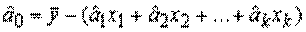
и осуществляется переход к исходной модели (5).

Тема 11. Общие требования к плану эксперимента. О критериях планирования эксперимента. Критерий ортогональности плана. Критерий ротатабельности. Критерий А-оптимальности. Критерий D-оптимальности. Критерий G-оптимальности.

Дата добавления: 2015-08-20