Распределение случайных ошибок измерения.

Вероятностная модель. Нормальный закон распределения. Показатели точности измерения.

Вероятностная модель. Случайные ошибки измерения характеризуются определенным законом их распределения. Существование такого закона можно обнаружить, повторяя много раз в неизменных условиях измерение некоторых величины и подсчитывая число m тех результатов измерения, которые в любой выделенный (отмеченный) интервал: отношение этого числа к общему числу n произведенных измерений (относительная частота попадания в отмеченный интервал) при достаточно большом числе измерений оказывается близким к постоянному числу (разумеется, своему для каждого интервала). Это обстоятельство позволяет применить к изучению случайных ошибок измерения методы теории вероятности. 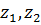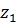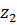В теоретико-вероятностной модели случайные ошибки z = x - a (а значит, и сами результаты измерения x = a - z) рассматриваются как случайные величины, которые могут принимать любые действительные значения, причем каждому интервалу () соответствует вполне определенное число, называемое вероятностью попадания случайной величины z в этот интервал и обозначаемое через Р( < z < ) или

Р(z Є (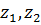)). Эта вероятность выступает как идеализированная относительная частота попадания в интервал (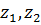), т.е. на практике именно к этой вероятности близки упомянутые выше относительные частоты:

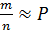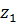( < z < ).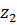

Правило, позволяющее для любых интервалов (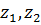) находить вероятности Р( 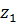< z < 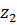), называются законом распределения вероятностей случайной величины z. Во всех задачах, рассматриваемых в настоящем справочном руководстве, закон распределения записывается с помощью интеграла

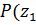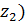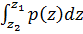< z < = , (1)

где p(z) – некоторая неотрицательная функция, нормированная условием

;

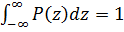эта функция полностью определяет соответствующий закон распределения вероятностей и называется плотностью распределения.

Нормальный закон распределения. В качестве закона распределения случайных ошибок измерения чаще всего принимают нормальный закон распределения (закон Гаусса). Плотность нормального распределения равна

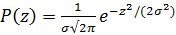, (2)

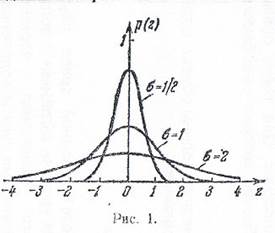
где параметр 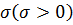характеризует точность измерений. График плотности распределения вероятностей называется кривой распределения. На рис.1 показаны кривые нормального распределения при различных значениях 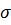; из этого рисунка видно, что при уменьшении параметра 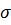кривая нормального распределения сжимается вдоль оси Oz и вытягивается вдоль оси p(z); и, следовательно, чем меньше 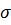, тем быстрее убывает плотность распределения p(z) с возрастанием .

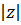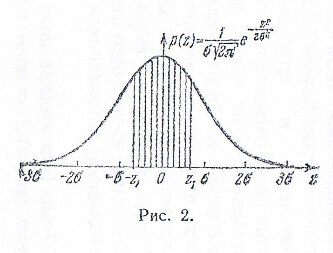
Вероятность (2) попадания в интервал 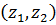графически изображается площадью соответствующей криволинейной трапеции под кривой распределения вероятностей. В частности, вероятность попадания в симметричный интервал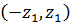 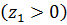изображается площадью фигуры, заштрихованной на рис. 2. Отсюда также видно, что чем меньше 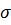, тем меньше разброс ошибок около нуля.

Вероятность попадания случайной ошибки в симметричный интервал 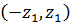при нормальном распределении вычисляется по формуле

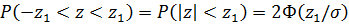, (3)

где

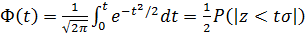(t > 0). (4)

Функция Ф(t) называется интегралом вероятностей, ее значения приведены в специальных таблицах. В этой таблице значения Ф(t) приведены лишь для положительных значений аргумента; для отрицательных значений аргумента функция Ф(t) продолжается нечетным образом:

Ф(t)=-Ф(t).

Вероятность попадания случайной ошибки в любой интервал 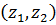в случае нормального распределения вычисляется по формуле

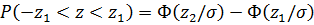. (5)

Наконец, вероятность того, что случайная ошибка выйдет за границы 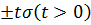, равна

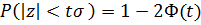. (6)

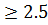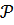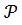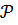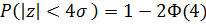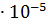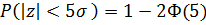Для удобства расчетов значения вероятностей 1-2Ф(t) при значения t приведены в таблице Там же даны значения и обратной функции t = t(), для которой 1- =1-2Ф(t), т.е. = 2Ф(t). При больших значениях t вероятность (6) очень мала. Например, =6 , =6 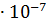. Уже вроятность выхода за трехсигмовые пределы

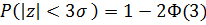=0,0027 (7)

настолько мала, что выход случайной ошибки измерения за трехсигмовые пределы считают практически невозможным (правило трех сигм). Другими словами, принимается, что случайные ошибки измерения ограничены по абсолютной величине значением 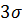(хотя рассматриваемая математическая модель допускает в принципе любые значения ошибок).

Нормальный закон распределения случайных ошибок обычно достаточно хорошо согласуется с опытом, что может быть проверено путем измерений известных величин (эталонов), когда можно точно подсчитать величины ошибок. В частности, нормальный закон отражает известное свойство симметрии случайных ошибок (случайные ошибки разных знаков встречаются примерно одинаково часто) и свойство концентрации (малые по абсолютной величине случайные ошибки встречаются чаще, чем большие).

Если в некоторой задаче возникает сомнение в нормальности закона распределения случайных ошибок (например, если случайные ошибки выходят за трехсигмовые пределы или если нарушается симметрия их распределения), то результаты измерения следует подвергнуть обработке.

Если случайные ошибки 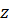имеют нормальный закон распределения с плотностью (2), то распределение результатов измерения x = a+z имеет плотность,

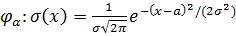, (8)

которая только сдвигом на величину a отличается от плотности (2). Этот закон распределения называется общим нормальным законом с центром a. Плотность (2) может быть записана, как 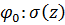. Для случайных ошибок всегда предполагается, что центр их распределения равен нулю.

Показатели точности измерения. Параметр 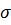(«сигма») называется средней квадратической ошибкой измерения, стандартной ошибкой или просто стандартом. Квадрат величины 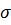называется дисперсией ошибки. Связь дисперсии с распределением вероятностей указана (4).

Кроме названных, иногда применяются и другие показатели точности измерений. Соотношения между различными показателями точности в случае нормального распределения ошибок следующие:

Вероятная ошибка

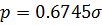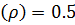, 2Ф (9)

Средняя абсолютная ошибка

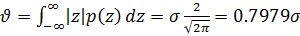(10)

Мера точности

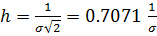. (11)

Дата добавления: 2015-08-20