Лекция 9.

Проверка нормальности распределения. Критерий соответствия χ² («хи-квадрат»). Приближенные методы проверки. Логарифмически нормальное распределение.

Проверка нормальности распределения

Все приведенные выше доверительные оценки как средних значений, так и дисперсий основаны на гипотезе нормальности закона распределения случайных ошибок измерения и поэтому могут применяться лишь до тех пор, пока результаты эксперимента не противоречат этой гипотезе.

Если результаты эксперимента вызывают сомнение в нормальности закона распределения случайных ошибок, то для решения вопроса о пригодности или непригодности нормального закона распределения надо произвести достаточно большое число измерений и применить один из описанных ниже критериев.

Критерий соответствия χ² («хи-квадрат»). Результаты измерений (разумеется, свободные от систематических ошибок) группируют по интервалам таким образом, чтобы эти интервалы покрывали всю ось (- ∞, + ∞) и чтобы количество данных в каждом интервале было достаточно большим (во всяком случае не менее пяти, лучше десяти). Для каждого интервала (х_i-1 x_i) под­считывают число m_i результатов измерения, попавших в этот интервал. Затем вычисляют вероятность р_i попадания в этот интервал при нормальном законе распределения вероятностей:

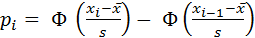, (1)

где - среднее арифметическое значение результатов измерения,

s - эмпирический стандарт (средняя квадра тическая ошибка),

Ф — интеграл вероятностей, представленный в (прилож, стр. 171 и 172).

Наконец, вычисляют сумму:

, (2)

где - число всех интервалов (-∞, х₁), (x₁, х₂), ….(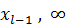) n - число всех результатов измерений (п = т_г + m₂ + … +m_i)/

Если сумма (2) окажется больше критического значения (прилож, стр. 179) при некоторой доверительной вероятности и числе степеней свободы k = l - 3, то с надежностью можно считать, что распределение вероятностей случайных ошибок в рассматриваемой серии измерений отличается от нор­мального. В противном случае для такого вывода нет достаточных оснований.

При отсутствии достаточных оснований для того, чтобы отвергнуть гипотезу о нормальном распределении случайных ошибок измерения, эта гипотеза принимается, так как в обычных ситуациях эта гипотеза часто может быть обоснована теоретически. Однако следует иметь в виду, что даже малая величина суммы (2) не может служить доказательством нормальности закона распределения.

Отметим еще важное свойство критерия если распределение отлично от нормального, то при достаточно большом числе измерений сумма (2) превысит соответствующее критическое значение 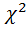. Поэтому, если при произведенном числе измерений критерий 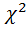дал малую надежность, но сомнение в нормальности распределения осталось, то следует увеличить число измерений (в несколько раз!).

Указанное выше число степеней свободы k = l - 3 относится только к тому случаю, когда оба параметра нормального закона распределения определяются по результатам измерений, т. е. когда вместо точных значений а и σ применяются их эмпирические значения 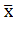и s. Если значение а точно известно (например, при измерении эталона), то число степеней свободы равно k = l - 2, если известны оба параметра а и σ, то число степеней свободы равно k = l — 1. На практике такая ситуация встречается редко, и поэтому для получения числа степеней свободы не менее пяти надо брать число интервалов не менее восьми.

В заключение заметим, что эффективность критерия повышается, если в каждый из выделенных интервалов попадает примерно одинаковое количество данных. Это следует учитывать при группировке первичного материала (если возможно).

Приближенные методы проверки. Применение критерия соответствия требует довольно значительных расчетов.

В качестве приближенного метода проверки нормальности распределения применяют метод, связанный с оценками центральных моментов третьего и четвертого порядков μ₃ и μ₄. В случае нормального распределения случайных ошибок эти моменты равны соответственно μ₃ = 0 и μ₄ = 3σ⁴. Оценками этих моментов по результатам эксперимента служат эмпирические центральные моменты М₃ и М₄. В случае нормального распределения должны выполняться приближенные равенства М₃ ≈ 0, M₄ ≈ 3s⁴. Для удобства сравнения подсчитывают безразмерные характеристики:

показатель асимметрии

g_s = M₃/ s³

и эксцесс

E = M₄/s⁴ -3

где s — эмпирический стандарт ошибки. Обе эти характеристики должны быть малы, если распределение нормально. О малости этих характеристик обычно судят по сравнению их с их средними квадратическими ошибками, соответственно равными

, для g_s,

, для Е

где n - количество измерений. Если хотя бы одна из указанных характеристик по абсолютной величине значительно (в 2—3 раза) превосходит свою среднюю квадратическую ошибку, то нормальность закона распределения следует подвергнуть сомнению и провести более тщательный анализ результатов эксперимента (например, с помощью критерия 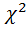). В противном случае для такого сомнения нет оснований.

Логарифмически нормальное распределение. В тех случаях, когда гипотеза о нормальном законе распределения оказывается в противоречии с экспериментальными данными (т. е. отвергается каким-либо из указанных выше критериев), применение оценок, изложенных в настоящей главе, может оказаться несостоятельным. Но иногда удается найти такое преобразование результатов измерения X_i что преобразованные величины Y_i = f (X_i) следуют нормальному закону распределения. В этом случае изложенные выше оценки можно применить к преобразованным величинам Y_i, а затем уже пересчитать их на величины X_i.

Например, часто встречается случай, когда нормальному распределению следуют не сами результаты измерения, а их логарифмы. Такой случай возникает тогда, когда факторы, искажающие результат измерения, вызывают эффект, пропорциональный самому результату измерения (т. е. когда устойчивыми в среднем оказываются не абсолютные, а относительные ошибки измерения). При этом говорят, что сам результат измерения X следует логарифмически нормальному распределению. Если обозначить ln Х = Y, т. е. X = e^Y, то из оценки центра распределения величины Y:

,

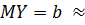
получается следующая оценка среднего значения величины X:

= ,

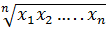это свидетельствует о целесообразности применения здесь не среднего арифметического, а среднего геометрического значения. Доверительная оценка для центра распределения величины Y _i, имеет вид

это приводит к следующей доверительной оценке для среднего значения величины X:

при больших n последнее соотношение т.е. может быть истолковано как оценка относительной ошибки.

Дата добавления: 2015-08-20