|
Читайте также: |
r i = 
; τист. = 
; r = −k∙ C 0A;
τист. =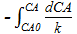 
= 
(CA)| = 
А−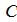 
А0) = 4,29.
РИВ
Fi =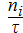 
; ω = 
; F i = ωi∙Ci, ; Ci, = 
; 
;
τист= 
= 4,3.
РИС
Fi = Fio+ 
∙FA0∙xA0;
r = 
= 
; V = 
;
τист.1 = 
= 
= 4,3.
Вывод: Таким образом, если реакция нулевого порядка, то время реакции в РПД, РИВ, РИС одинакова.
Пример 3. Газофазная реакция получения продукта по схеме А→2 R
−rA = 6,57∙10-4∙C A0.7 кмоль/м3с, Т = 150 0 С, р =3,5 атм.
Исходное сырье не содержит продукта R, но имеет 12 % по объему инертных примесей. Объемная скорость подачи сырья ω0 = 5,6∙10-3 м3 /с.
Определить:
1.Степень превращения в РИВ, если VРИВ = 3 м3;
2.Степень превращения в РПД с VРПД = 2 м3, время загрузки и выгрузки составляет 10 % от времени реакции.
Найти для второго случая время протекания ХТП.
Решение. А→2 R с изменением объема,
В условии задачи часто не прописывается, что реакция идет с изменением объема. Однако объем нужно учесть если:
1.В условии газофазная реакция и сумма молей исходных реагентов не равна сумме продуктов.
2.Если в условии сказано, что реакция протекает с изменением плотности веществ- участников реакций.
Сi =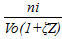 
;
V = V0(1+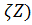 
;
= 
;
= 0,88;
z = xA; V = V0(1 + 
;
τист = 
; −rA = 6,57∙10-4∙C A0.7 кмоль/м3с;
CA=CAo+ 
∙CAo∙xA= CAo(1−xA);
dCA=CAo 
(1−xA);
dCA=−CAo dxA ;
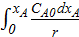τ = − 
= − 
;
τ = 
; τ =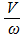 
= 
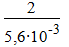= 357,14;
Уравнение Ван-дер- Ваальса
PV = nRT; P = 
RT= CRT;
CA0 = 
= 
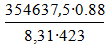= 88,78∙10-2 ;
τ = 357 = 
; 
;
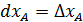357 = 
Задача далее решается подбором значения х А , подставим значения 0,1 0,2 и т.д. Перебирая значения хА подставляют в α и смотрят, численное значение, полученное в правой части уравнения.
Для РПД степень превращения будет точно такой же как в РИВ. (хА =0,86), а время 357 сек., τхтп =357+35,7=392,7;
τ = 357 
= 
;
если без изменения объема, то СА = 
;
CA = CA0(1−xA); без изменения объема,
СА =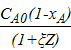 
; с изменением объема.
С изменением объема r = 6.5∙10-4 (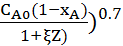
;
dCA = d(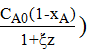 
;
С изменением объема V = V0(1+ξz);
ξ = 
;
CA = 
= 
= 
;
По уравнение Клайперона СА0 = 88.78∙10-2;
Характеристическое уравнение РИВ
τ = 
= 357 = 
;
dCA = d [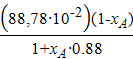 
] = 88.78∙10-2 d( 
) = = 
;
;
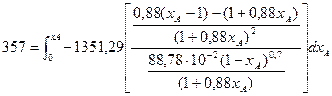Для РПД интеграл получится таким же, как и в первом случае.
Если был бы РИС, то
τис т = 357 =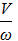 
= 
= 
= 
;
Далее задача решается методом подбора.
Пример 4. Какую размерность имеет константа скоростей кинетических уравнений.
а) r = 
;
б) r = 
;
Дата добавления: 2015-08-17; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Решение. |