Теорема Таубера

Теорема. Пусть ряд (1) сходится при 0<x<1, и имеет место предельное равенство (5). Если члены ряда (А) таковы, что

( 6)

то и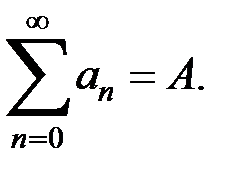

Доказательство. Разобьем доказательство на две части. Сначала

предположим, что Если положить то при величина , монотонно убывая, стремится к нулю.

Имеем при любом натуральном N

так что:

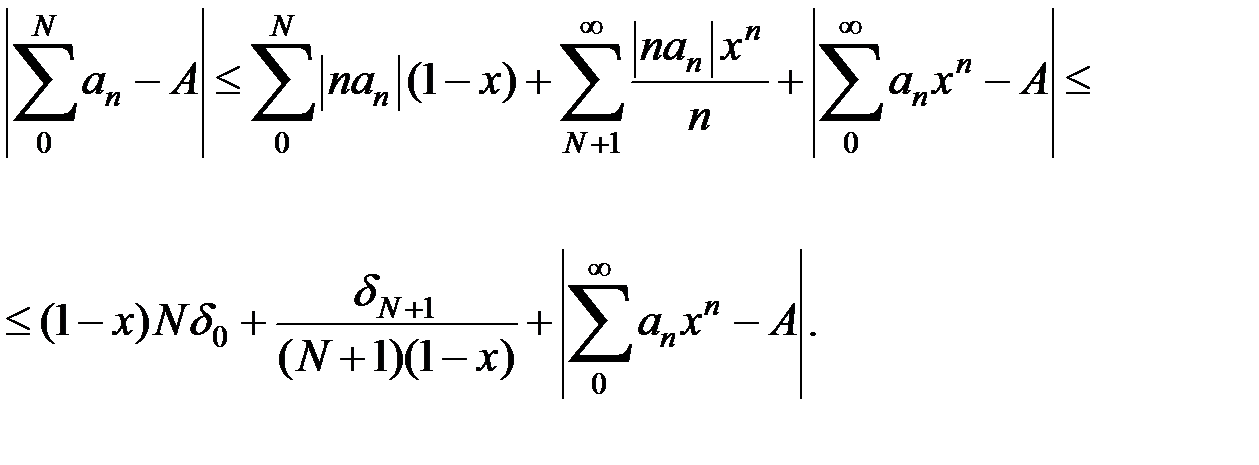
Взяв произвольно малое число 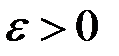, положим

Так что при . Пусть теперь 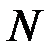выбрано достаточно большим чтобы: выполнялось неравенство ; соответствующее x было настолько близко к 1, что

. Тогда

Что и доказывает утверждение теоремы.

Дата добавления: 2015-08-17