Истоки проблемы

Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования рядов, в некоем новом смысле”.

Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ряды нередко встречались в математической практике.

Хотя применение их при доказательствах и оспаривалось, тем не менее иной раз делались попытки придавать им даже числовой смысл.

Вспомним, опять, наш колеблющийся ряд

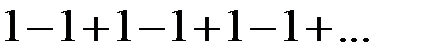
Еще со времен Лейбница в качестве "суммы" приписывалось число . Эйлер, например, мотивировал это тем, что из разложения

(которое в действительности имеет место лишь для ) при подстановке вместо х единицы как раз и получается

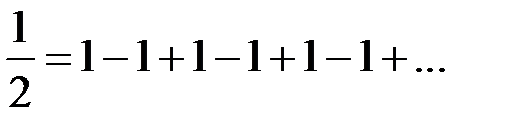
В этом уже содержалась истина, но постановке вопроса не хватало четкости; самый произвол в выборе разложения оставлял открытой возможность из другого разложения (где п и т - любые, но )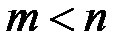

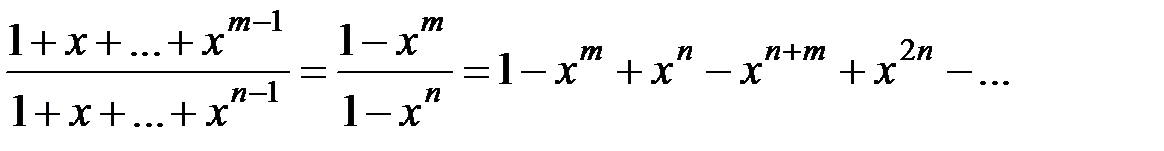
получить одновременно

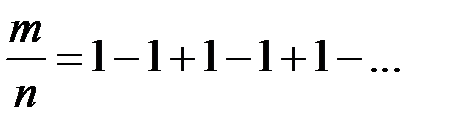
Современный анализ ставит вопрос по-другому. В основу кладется то или иное точно сформулированное определение “обобщенной суммы" ряда, придуманное не только для конкретно интересующего нас числового ряда, но приложимое к целому ряду классов таких рядов. Определение “обобщенной суммы" обычно подчиняется двум требованиям.

Во-первых, если ряду 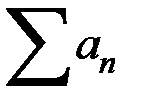приписывается “обобщенная сумма" А, а ряду 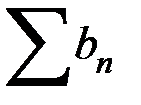- “обобщенная сумма" В, то ряд 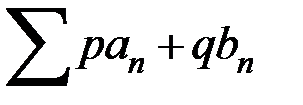, где p, q - две произвольные постоянные, то должен иметь в качестве “обобщенной суммы" число 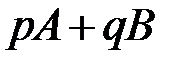. Метод суммирования, удовлетворяющий этому требованию, называется линейным.

Во-вторых, новое определение должно содержать обычное определение как частный случай. То есть, ряд, сходящийся в обычном смысле к сумме А, должен иметь “обобщенную сумму", и притом также равную А. Метод суммирования, обладающий этим свойством, называют регулярным. Разумеется, интерес представляют лишь такие регулярные методы, которые позволяют устанавливать “сумму” в более широком классе случаев, нежели обычный метод суммирования: лишь тогда с полным правом можно говорить об “обобщенном суммировании”. Мы переходим к теперь непосредственно к рассмотрению особо важных с точки зрения приложений методов ‘обобщенного суммирования".

Дата добавления: 2015-08-17