Читайте также:
|
Он состоит в следующем: по ряду (А) и его частичным суммам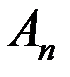 
строится выражение:
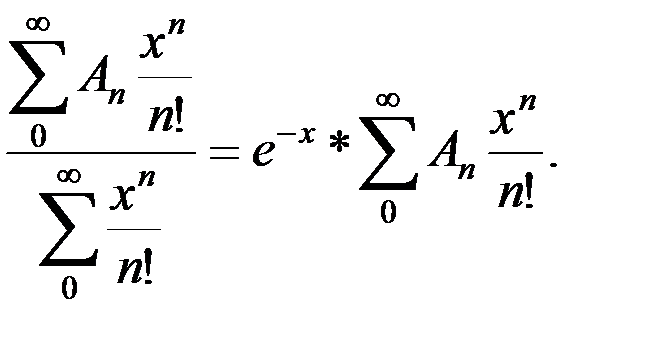
Если последний ряд сходится, хотя бы для достаточно больших значений х, и его сумма при 
имеет предел А, то это число и является “обобщенной суммой” в смысле Борелядля данного ряда (А).
Докажем регулярность метода Бореля. Допустим сходимость ряда (А) и обозначим его сумму через А, а остатки 
через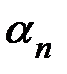 
. Имеем (для достаточно больших х)
Зададимся произвольно малым числом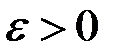 
; найдется такой номер N, что для 
будет:
.
Представим последнее выражение в виде суммы,
.
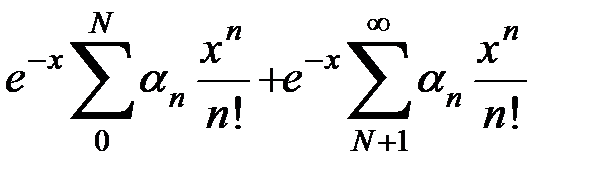Второе слагаемое по абсолютной величине 
, каково бы ни было х, а первое представляющее собой произведение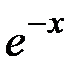 
на многочлен, целый относительно х, становится абсолютно при достаточно больших х. Этим все доказано.
Дата добавления: 2015-08-17; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обобщенные методы Чезаро | | | Метод Эйлера |