Теорема Абеля. Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле)

Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле), то для 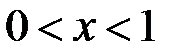сходится степенной ряд (1), и его сумма стремится к пределу А, когда .

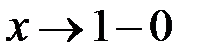Доказательство. Начнем с того, что радиус сходимости ряда (1) не меньше 1, так что для 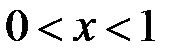ряд (1), действительно, сходится. Мы имели уже тождество

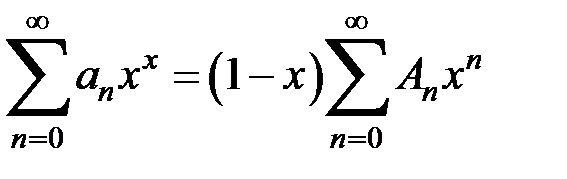
( где 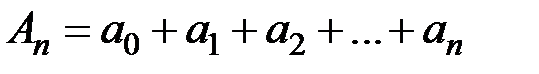); вычтем его почленно из тождества

.

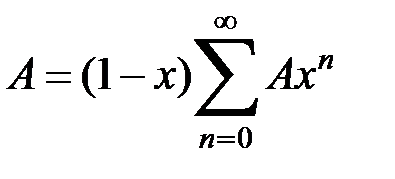Полагая 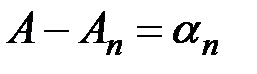, Придем к тождеству

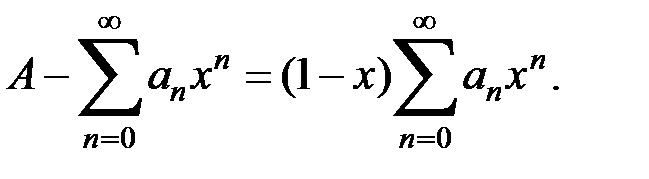(4)

Так как 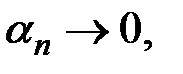то по произвольно заданному 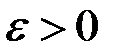найдется такой номер 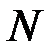, что 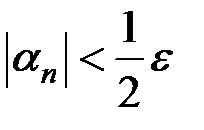, лишь только .

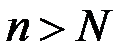Разобьем сумму ряда в правой части (4) на две суммы

Вторая оценивается сразу и независимо от :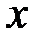

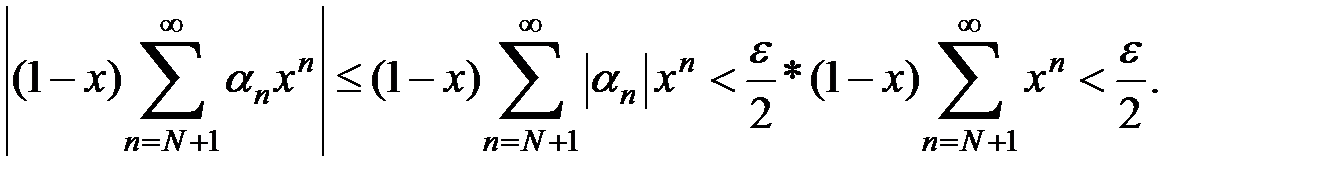
Что же касается первой, то она стремится к 0 при 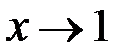и при достаточной близости 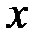к 1 будет

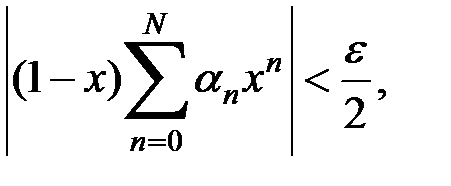
так что окончательно 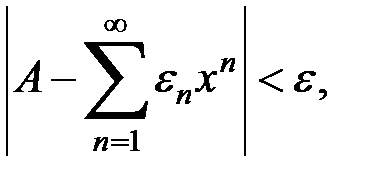что и доказывает утверждение.

Если ряд (А) суммируем по Пуассону-Абелю к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы. Иными словами из существования предела

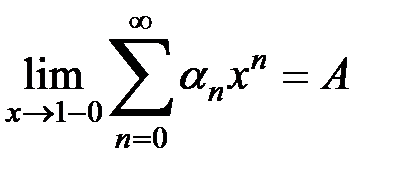, (5)

вообще говоря, не вытекает сходимость ряда (А). Естественно возникает вопрос, какие дополнительные условия надлежит наложить на поведение членов этого ряда, чтобы из (5) можно было заключить о сходимости ряда (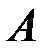), т.е. о существовании для него суммы 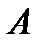в обычном смысле. Первая теорема в этом направлении была доказана Таубером.

Дата добавления: 2015-08-17