
|
Читайте также: |
Элементарной работой силы  называется скалярная величина:
называется скалярная величина:
 ,
,
где  - проекция силы
- проекция силы  на касательную к траектории, направленную в сторону перемещения точки, а ds- бесконечно малое перемещение точки, направленное вдоль этой касательной.
на касательную к траектории, направленную в сторону перемещения точки, а ds- бесконечно малое перемещение точки, направленное вдоль этой касательной.
Данное определение соответствует понятию о работе, как о характеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу  на составляющие
на составляющие 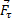 и
и  , то изменять модуль скорости точки будет только составляющая
, то изменять модуль скорости точки будет только составляющая 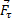 , сообщающая точке касательное ускорение. Составляющая же
, сообщающая точке касательное ускорение. Составляющая же  или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном движение изменяет давление на связь. На модуль скорости составляющая
или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном движение изменяет давление на связь. На модуль скорости составляющая  влиять не будет, т.е., как говорят, сила
влиять не будет, т.е., как говорят, сила  «не будет производить работу».
«не будет производить работу».
Замечая, что  , получаем:
, получаем:
 .
.
Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементарное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.
(51) Работа силы на конечных перемещениях

Работа силы на конечном перемещении определяется как интегральная сумма элементарных работ и при перемещении M 0 M 1выражается криволинейным интегралом:

или
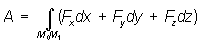
Дата добавления: 2015-08-17; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Момент силы относительно точки и оси | | | Парадигмы социального знания. |