
Читайте также:
|
Рассмотрим, как вычисляются скорость и ускорение точки при задании ее движения в полярных координатах, то есть когда заданы уравнения движения точки в виде r = r(t);  =
=  (t).
(t).
Вектор ускорения a точки направлен в сторону вогнутости траектории и определяется своими проекциями ar и 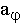 на оси Pr и P
на оси Pr и P  по формулам:
по формулам:
ar = d2r/dt2 - r (d  /dt)2 =
/dt)2 = 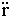 - r (
- r ( )2;
)2;
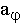 = r (d2
= r (d2  /dt2) + 2 (dr/dt) (d
/dt2) + 2 (dr/dt) (d  /dt) = r
/dt) = r 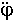 + 2
+ 2 
 .
.
Величины ar и 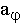 соответственно называются радиальным и трансверсальным ускорениями точки.
соответственно называются радиальным и трансверсальным ускорениями точки.

Дата добавления: 2015-08-17; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Связь полярных и декартовых координат. | | | Абсолютное ускорение точки |