Что такое циклоида.

Цикло́ида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса , катящейся без скольжения по прямой.

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса .

· Циклоида описывается параметрически

,

.

· Уравнение в декартовых координатах:

· Циклоида может быть получена как решение дифференциального уравнения:

29 Ускорение Кориолиса

Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e * ν_r, где ω _e - переносная угловая скорость, ν_r - относительная скорость точки. Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского. Величина ускорения Кориолиса определяется выражением a_C = 2 ω_e ν_r sinα,где α – угол между векторами ω_e и ν_r.

Ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

30 Неподвижная центроида

ЦЕНТРОИДА - геом. место мгновенных центров вращения при движении неизменяемой плоской фигуры в её плоскости. На неподвижной плоскости это геом. место образует неподвижную Ц., а на плоскости, движущейся вместе с фигурой,- подвижную Ц. В каждый момент времени эти Ц. касаются друг друга в точке, являющейся для этого момента мгновенным центром вращения. Движение фигуры в её плоскости можно осуществить качением без скольжения подвижной Ц. по неподвижной.

31 НЦУ

31. МЦУ

При движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нулю. Эту точку называют мгновенным центром ускорений (МЦУ). Для того чтобы определить МЦУ, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами . В точке пересечения проведённых прямых и будет находиться мгновенный центр ускорений. Угол должен удовлетворять равенству:

где

— угловое ускорение тела;

— угловая скорость тела.

32 Нормальная составляющая вектора скорости точки

При движении тела по криволинейной траектории его скорость изменяется по модулю и направлению. Изменение вектора скорости за некоторый малый промежуток времени Δ t можно задать с помощью вектора 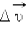(рис. 1.1.4).Вектор изменения скорости 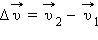за малое время Δ t можно разложить на две составляющие: 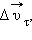направленную вдоль вектора (касательная составляющая), и 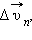направленную перпендикулярно вектору (нормальная составляющая).

Рисунок 1.1.4. Изменение вектора скорости по величине и направлению. – изменение вектора скорости за время

33, 34?

Дата добавления: 2015-08-17