
|
Читайте также: |
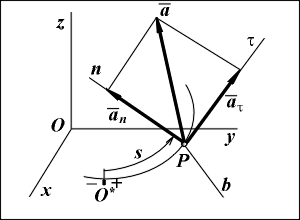 Вектор ускорения
Вектор ускорения 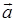 точки лежит в соприкасающейся плоскости
точки лежит в соприкасающейся плоскости 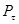 и определяется двумя проекциями
и определяется двумя проекциями 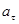 и
и 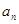 (
(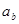 = 0):
= 0):
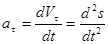 или
или 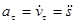 .
.
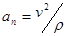 .
.Величины 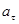 и
и 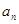 соответственно называют касательным и нормальным ускорениями точки.
соответственно называют касательным и нормальным ускорениями точки.
Вектор ускорения 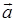 является векторной суммой касательной составляющей
является векторной суммой касательной составляющей 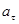 , направленной вдоль касательной
, направленной вдоль касательной 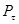 , и нормальной составляющей
, и нормальной составляющей 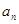 , направленной вдоль главной нормали
, направленной вдоль главной нормали 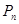 :
: 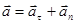 .
.
Так как эти составляющие взаимно перпендикулярны, то модуль вектора 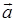 определяется по формуле:
определяется по формуле: 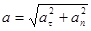 .
.
14. Чему равна производная от вектора постоянного по модуля по скалярному аргументу?
Производная постоянного по модулю вектора по скалярному аргументу есть вектор, перпендикулярный исходному.
Дата добавления: 2015-08-17; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула Ривальса | | | Связь полярных и декартовых координат. |