|
Читайте также: |
17. Движение тела может рассматриваться как результат сложения поступательного движения и вращения тела относительно одной из точек тела, называемой полюсом.
18. Трансверсальная составляющая ускорения точки
Ускорение точки: 
, где 
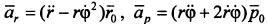- радиальная и трансверсальная составляющие ускорения точки соответственно. Так как составляющие ускорения взаимно перпендикулярны, то его модуль: 
.
19. С оставляющая же ускорения 
не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой.
Таким образом, имеем:
Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного 
.
Используя обозначения 
и 
, получим запись теоремы Кориолиса в более сжатом виде:
Дата добавления: 2015-08-17; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вектор ускорения точки при естественном способе задания движения. | | | Радиальная составляющая вектора ускорения |