Две задачи динамики точки

1. Первая задача состоит в том, чтобы по заданному закону движения точки массой m определить силу, под действием которой происходит это движение. Часто первую задачу рассматривают как задачу управления движением, в рамках которой требуется установить характеристики воздействия, обеспечивающие заданный закон движения материальной точки. В зависимости от способа задания движения при решении этой задачи используют соответствующие скалярные уравнения.

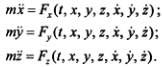(13.3)

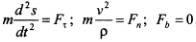
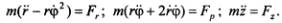
2. Вторая задача состоит в определении движения точки по заданным силам и начальным условиям движения, при этом силы должны быть выражены как функции переменных, используемых для задания движения. Решение этой задачи сводится к интегрированию дифференциальных уравнений второго порядка, в процессе которого в решениях появляются произвольные постоянные, подлежащие определению. Так, в задаче о движении точки в трехмерном пространстве, решаемой на основе дифференциальных уравнений 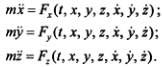, общие решения будут содержать шесть произвольных постоянных:

,

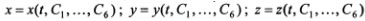для определения которых потребуется постановка дополнительных условий. Из математики известно, что если эти условия поставлены для начальных (при t = 0) значений функций и их первых производных, т. е. в виде x(0)=х₀, y(0)=у₀, z(0)=z₀, 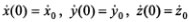,то задача (задача Коши) при некоторых ограничениях, налагаемых на правые части дифференциальных уравнений, имеет решение и причем единственное. Таким образом, приложенные к точке силы определяют только ее ускорение, движение же точки помимо сил зависит от начальных условий — положения точки в рассматриваемой инерциальной системе отсчета и ее скорости.

Две основные задачи динамики точки (из лекций):

1. Прямая: Зная m и действующую силу, определим движение материальной точки.

2. Обратная: Зная m материальной точки и ее уравнение движения, можно найти действующую на точку силу.

Дата добавления: 2015-08-17