Статистическая обработка результатов прямых измерений

Допустим, что было выполнено 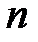измерений какой-либо физической величины (время, длина и т.д.) и результат записан в таблицу. Вследствие случайных факторов, в общем случае, получится совокупность 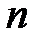различных значений одной и той же величины :

.

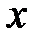По результатам 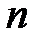измерений вычисляют среднее выборочное (см. (12.3)) и проверяют результаты измерений на промахи. Результат , принадлежащий нормальному распределению, считается с вероятностью 95% промахом, если

, (12.7)

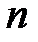где – величина выборочного среднеквадратичного отклонения (12.4), а в зависимости от принимает значения, приведённые в следующей таблице:

Таблица 12.2

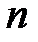
	1,41	1,69	1,87	2,0	2,09	2,17	2,24	2,29	2,34	2,39	2,49	2,62	2,80	3,20

Исключив промахи, снова вычисляют среднее выборочное , с изменённым соответственно .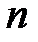

Вычисляют среднее квадратичное отклонение 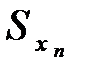по формуле

, (12.8)

здесь и далее 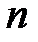– объём выборки с исключёнными промахами.

Задаваясь доверительной вероятностью , определяют по табл. 12.3 коэффициент Стьюдента и .

Оценивая погрешность приборов и табличных величин при ликвидации других систематических погрешностей, если они есть, вычисляют абсолютную погрешность по формуле

(12.9)

в случае если приборная и случайная погрешность одного порядка, то есть при

Таблица 12.3

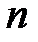
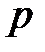
	6,31	12,71	31,82	63,66
	2,92	4,30	6,96	9,92
	2,35	3,18	4,54	5,84
	2,13	2,78	3,75	4,60
	2,02	2,57	3,36	4,03
	1,92	2,54	3,14	3,71
	1,89	2,36	3,00	3,50
	1,86	2,21	2,90	3,36
	1,83	2,26	2,28	3,23
	1,81	2,23	2,76	3,17
	1,80	2,20	2,72	3,11
	1,78	2,18	2,68	3,05
	1,77	2,16	2,65	3,01
	1,76	2,14	2,62	2,98
	1,75	2,13	2,60	2,95
	1,75	2,12	2,56	2,92
	1,74	2,11	2,57	2,90
	1,73	2,10	2,55	2,88
	1,73	2,09	2,54	2,86
	1,67	2,00	–	2,66
	1,66	1,98	–	2,62
	1,65	1,96	2,33	2,58

В предельных случаях:

1) если , то в (12.9) приборной погрешностью пренебрегают, тогда ;

2) если , то в (12.9) пренебрегают случайной погрешностью, тогда .

Далее, вычисляют относительную погрешность по формуле

. (12.10)

Относительная погрешность вводится для оценки точности измерений. Формула (12.10) удобна при сравнении точности измерений различных физических величин в одном эксперименте или одной величины разными приборами (или методами).

Округляя численные значения результата и погрешности, записывают окончательный результат в виде

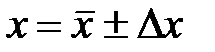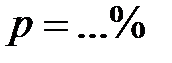, , . (12.11)

Дата добавления: 2015-08-17