
|
Читайте также: |
Цель работы – изучение равновесных термодинамических процессов в идеальных газах, определение показателя адиабаты для воздуха классическим методом Клемана и Дезорма.
Описание экспериментальной установки
Установка для измерения показателя адиабаты методом Клемана и Дезорма содержит стеклянный сосуд 1 с пробкой 2, в которой установлены подпружиненный клапан 3, а также соединительные трубки жидкостного U -образного манометра 4 и ручного насоса 5, который сообщается с сосудом через вентиль 6. Схема установки показананарис.10.1.
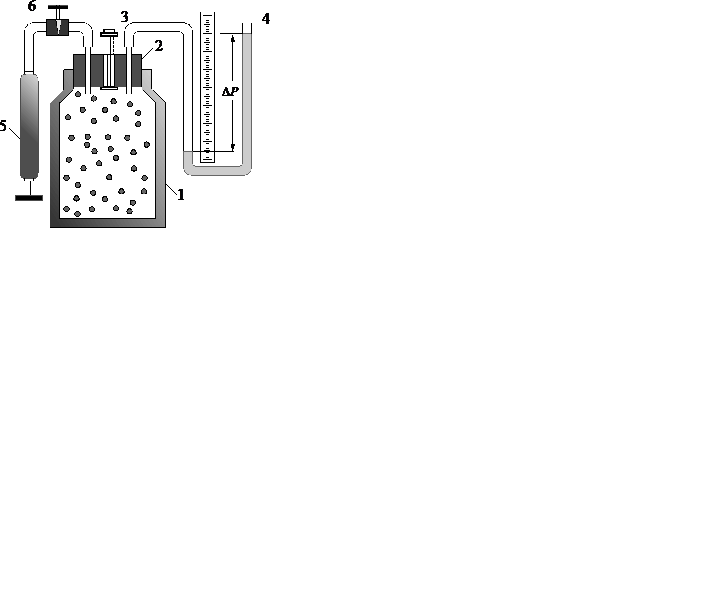
Рис.10.1
Методика эксперимента и вывод рабочих формул
Газ, находящийся в некотором замкнутом объеме, можно считать идеальным, если он удовлетворяет следующим условиям:
1) cобственный объем молекул газа много меньше объема сосуда, в который газ помещен;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Многие реальные газы (например, водород, гелий, неон, азот, кислород, воздух и др.) в условиях, близких к нормальным, близки по своим свойствам к идеальному газу. Кроме того, если внести поправки на объем молекул и молекулярные силы, от теории идеального газа можно перейти к теории реального газа.
Опытным путем до создания молекулярно-кинетической теории был открыт целый ряд законов, которым удовлетворяет идеальный газ.
Закон Гей-Люссака: объем данной массы газа ( ) при постоянном давлении (
) при постоянном давлении (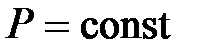 ) изменяется линейно с температурой:
) изменяется линейно с температурой:
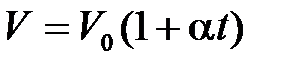 ,
,
где 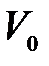 – объем газа при нулевой температуре (
– объем газа при нулевой температуре (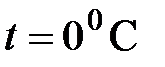 ), а
), а 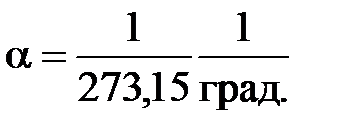 .
.
Процесс, протекающий при постоянном давлении, называется изобарическим (изобарным).
Закон Шарля: давление данной массы газа ( ) при постоянном объеме (
) при постоянном объеме (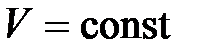 ) изменяется линейно с температурой:
) изменяется линейно с температурой:
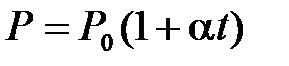 ,
,
где 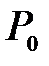 – объем при
– объем при 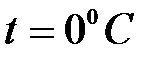 .
.
Процесс, протекающий при постоянном объеме, называется изохорическим (изохорным).
С введением термодинамической температуры T, выраженной в кельвинах (К):
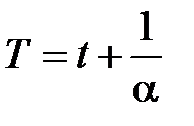 ,
,
законы Гей-Люссака и Шарля можно переписать в виде
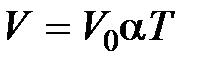 при
при 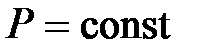 ,
, 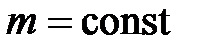
и
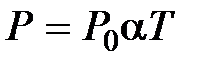 при
при  ,
, 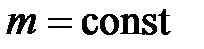 ;
;
или
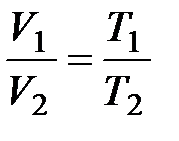 (
( ,
, 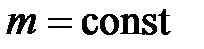 ); (10.1)
); (10.1)
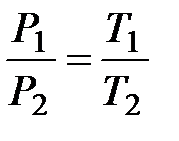 (
(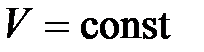 ,
, 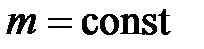 ). (10.2)
). (10.2)
Закон Бойля – Мариотта: для данной массы газа (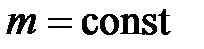 ) при постоянной температуре (
) при постоянной температуре (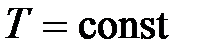 ) произведение давления газа на его объем есть величина постоянная:
) произведение давления газа на его объем есть величина постоянная:
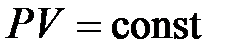 . (10.3)
. (10.3)
Процесс, протекающий при постоянной температуре, называется изотермическим.
Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы.
При нормальных условиях (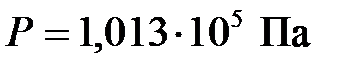 ,
,  ) этот объем составляет
) этот объем составляет 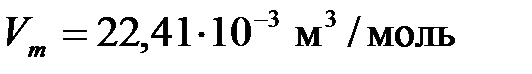 .
.
Моль – единица количества вещества в СИ. В одном моле содержится столько атомов (молекул, ионов), сколько атомов содержится в 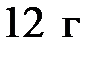 изотопа углерода с атомным весом
изотопа углерода с атомным весом  .
.
Из изложенного следует, что в одном моле различных веществ содержится одно и то же число молекул, которое называется числом Авогадро: 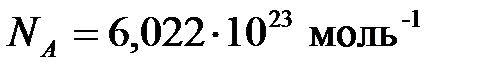 .
.
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов:
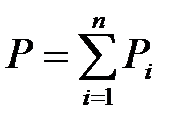 .
.
Парциальное давление (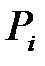 ) – давление, которое производил бы i -й газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
) – давление, которое производил бы i -й газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
Поскольку состояние с фиксированной массой газа определяется тремя параметрами ( ), можно составить уравнение, устанавливающее связь между этими параметрами:
), можно составить уравнение, устанавливающее связь между этими параметрами:
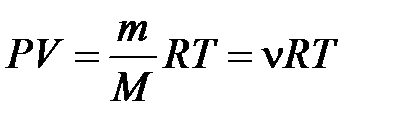 , (10.4)
, (10.4)
где  – количество молей газа;
– количество молей газа; 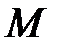 – масса одного моля газа;
– масса одного моля газа; 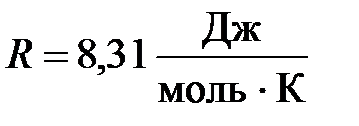 – одинаковая для всех газов величина, называемая универсальной газовой постоянной.
– одинаковая для всех газов величина, называемая универсальной газовой постоянной.
Уравнение (10.4) называется уравнением состояния идеального газа или уравнением Менделеева – Клапейрона.
Состояние термодинамической системы называют стационарным, если оно не изменяется во времени. Стационарное состояние называется равновесным, если неизменность системы во времени не обусловлена внешним воздействием.
Термодинамическое равновесие двух систем (или двух частей одной системы) характеризуется тем, что обе системы (части системы) имеют одинаковую температуру.
Идеальный газ, как и любая макроскопическая система, состоит из большого числа молекул (атомов), двигающихся и взаимодействующих друг с другом. Эта энергия всевозможных видов движения и взаимодействия микрочастиц (атомов, молекул, электронов, ядер и т.д.), образующих макроскопическую систему, называется внутренней энергией. Внутренняя энергия системы тел равна сумме внутренних энергий каждого из тел в отдельности и энергии взаимодействия между телами. Последняя столь мала по сравнению с внутренней энергией макроскопических тел, что ею можно пренебречь.
Для идеального газа внутренняя энергия определяется как
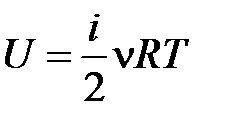 , (10.5)
, (10.5)
где 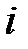 – количество степеней свободы молекул газа. Для одноатомного газа
– количество степеней свободы молекул газа. Для одноатомного газа  для двухатомного с жесткой связью между молекулами –
для двухатомного с жесткой связью между молекулами – 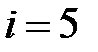 , для многоатомного газа с жесткой связью между молекулами –
, для многоатомного газа с жесткой связью между молекулами – 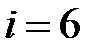 .
.
Обмен энергией между термодинамической системой и внешними телами может происходить двумя способами:
1) при совершении работы;
2) с помощью теплообмена.
Количество энергии, переданное системе внешними телами при силовом взаимодействии между ними, называется работой, совершенной над системой.
Полную работу  , совершаемую газом при изменении его объема от
, совершаемую газом при изменении его объема от 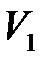 до
до 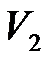 , можно найти по формуле:
, можно найти по формуле:
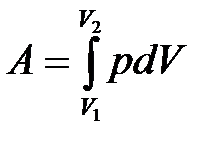 . (10.6)
. (10.6)
Количество энергии, переданное системе внешними телами путем теплообмена, называется количеством теплоты, сообщенной системе.
Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания одного моля вещества на  :
:
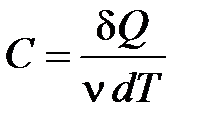 , (10.7)
, (10.7)
Из (10.7) для теплоемкости газа при изохорном процессе имеем:
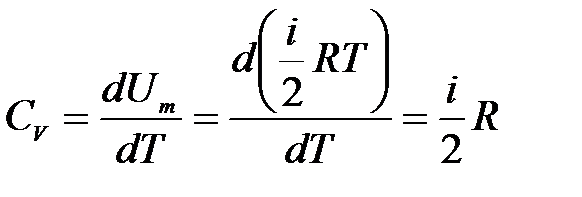 , (10.8)
, (10.8)
при изобарном процессе:
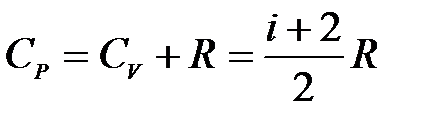 . (10.9)
. (10.9)
Работа и теплота являются энергетическими характеристиками процессов изменения состояния термодинамической системы и имеют смысл только при наличии таких процессов. Работа и теплота не являются видами энергии, поэтому нельзя говорить о запасе работы или запасе теплоты. Совершение работы над системой может изменить любой вид энергии системы: и внутреннюю, и кинетическую энергию системы как целого. Если энергия сообщается в форме теплоты, то она идет на увеличение внутренней энергии.
В зависимости от вида взаимодействия термодинамической системы с внешней средой выделяют следующие типы термодинамических систем.
Открытой называется термодинамическая система, которая может взаимодействовать с внешней средой.
Изолированной называется термодинамическая система, которая не может обмениваться с внешней средой ни энергией, ни веществом.
Замкнутой называется термодинамическая система, не способная к обмену энергией с внешней средой путем совершения работы.
Термодинамическая система называется адиабатической, если не происходит теплообмена между системой и внешней средой. При этом система может совершать работу против внешних сил или внешние силы могут совершать работу над ней.
За счет обмена энергией с внешней средой термодинамическая система переходит из одного состояния в другое, то есть совершается термодинамический процесс. При этом количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы против внешних сил:
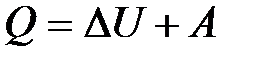 , (10.10)
, (10.10)
где 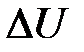 – изменение внутренней энергии системы;
– изменение внутренней энергии системы; 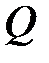 – подводимое к системе тепло;
– подводимое к системе тепло;  – работа, совершаемая системой против внешних сил. Если
– работа, совершаемая системой против внешних сил. Если 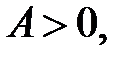 то работу совершает система, если
то работу совершает система, если  , то работа совершается над системой.
, то работа совершается над системой.
Формула (10.10) представляет собой интегральную форму записи первого начала термодинамики.
В дифференциальной форме записи первое начало термодинамики имеет вид
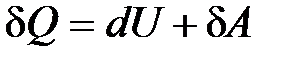 , (10.11)
, (10.11)
где 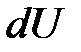 – элементарное (бесконечно малое) изменение внутренней энергии системы;
– элементарное (бесконечно малое) изменение внутренней энергии системы; 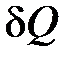 – элементарное подводимое к системе тепло (бесконечно малое количество теплоты);
– элементарное подводимое к системе тепло (бесконечно малое количество теплоты); 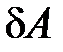 – элементарная работа, совершаемая системой.
– элементарная работа, совершаемая системой.
Термодинамический процесс называется равновесным (квазистатическим), если система бесконечно медленно проходит непрерывный ряд бесконечно близких (термодинамически) равновесных состояний.
Изотермический процесс протекает при постоянной температуре системы и принципиально является равновесным. Реально тепловые процессы, включая изобарический и изохорический, проводят более или менее быстро. В ряде случаев их можно рассматривать как равновесные только приближенно. Процессы, которые в определенных условиях с некоторым приближением можно рассматривать как равновесные, называют квазиравновесными, например, квазиравновесный адиабатический (адиабатный) процесс.
Адиабатический процесс – процесс, происходящий без теплообмена с внешней средой ( ). Для этого система должна быть термодинамически изолирована.
). Для этого система должна быть термодинамически изолирована.
На практике адиабатный процесс проводят как процесс квазиравновесный: объем системы изменяют настолько быстро, чтобы за время длительности процесса можно было пренебречь теплообменом системы с внешней средой, т.е. 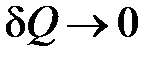 .
.
Адиабатный процесс в идеальном газе с постоянным числом одинаковых молекул аналитически описывается уравнением
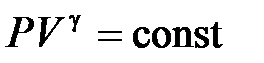 , (10.12)
, (10.12)
где показатель адиабаты 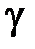 определяется только числом степеней свободы
определяется только числом степеней свободы 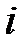 молекулы газа и равен отношению теплоемкостей газа при постоянном давлении
молекулы газа и равен отношению теплоемкостей газа при постоянном давлении 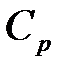 (изобарический процесс) и при постоянном объеме
(изобарический процесс) и при постоянном объеме 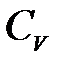 (изохорический процесс):
(изохорический процесс):
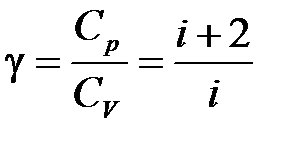 . (10.13)
. (10.13)
Наиболее просто с технической точки зрения осуществляется процесс адиабатного расширения газа из равновесного состояния 1, при котором температура системы 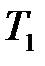 равна температуре
равна температуре 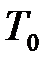 окружающей внешней среды, а давление
окружающей внешней среды, а давление 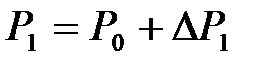 превышает значение атмосферного давления
превышает значение атмосферного давления 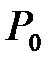 . По окончании адиабатного процесса в квазиравновесном состоянии 2 температура будет
. По окончании адиабатного процесса в квазиравновесном состоянии 2 температура будет 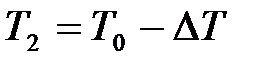 , а давление в системе
, а давление в системе 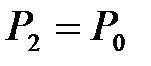 (рис.10.2).
(рис.10.2).
Для эксперимента необходима система, способная спонтанно увеличить свой объем при неизменном количестве вещества. Такая система не может быть ограничена стенками какого-либо сосуда, имеющего постоянный объем. В то же время избыточное давление в системе можно обеспечить только тогда, когда она заключена в таком сосуде. Для устранения этого противоречия выберем систему молекул, находящуюся внутри сосуда, но занимающую при избыточном давлении 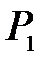 только небольшую часть
только небольшую часть 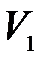 объема сосуда, как показано на рис. 10.2, где выделенная система условно ограничена круговой линией.
объема сосуда, как показано на рис. 10.2, где выделенная система условно ограничена круговой линией.

Рис.10.2
В исходное равновесное состояние 1 система приходит после предварительного сжатия (подкачка газа может быть осуществлена насосом) и последующей релаксации (в течение нескольких минут), когда в условиях теплового равновесия с внешней средой весь газ в сосуде будет иметь температуру 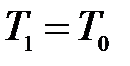 и установившееся давление
и установившееся давление 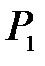 .
.
В процессе быстрого адиабатного расширения системы, производимого резким соединением через открывающийся клапан 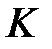 полости сосуда с внешней средой, теплообменом газа в сосуде и, тем более, в выделенной системе, можно пренебречь (
полости сосуда с внешней средой, теплообменом газа в сосуде и, тем более, в выделенной системе, можно пренебречь (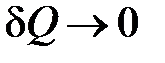 ). Внутренняя энергия системы уменьшается на величину
). Внутренняя энергия системы уменьшается на величину 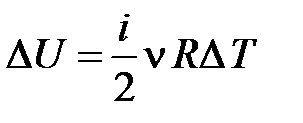 , расходуемую на работу
, расходуемую на работу 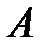 расширения системы:
расширения системы: 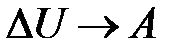 . На диаграмме (рис. 10.3) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
. На диаграмме (рис. 10.3) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
Из уравнения адиабатного процесса для состояний 1 и 2 имеем
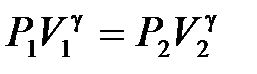 , (10.14)
, (10.14)
но так как 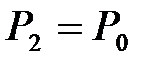 , то можно записать, что
, то можно записать, что 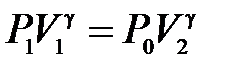 . Откуда показатель адиабаты
. Откуда показатель адиабаты
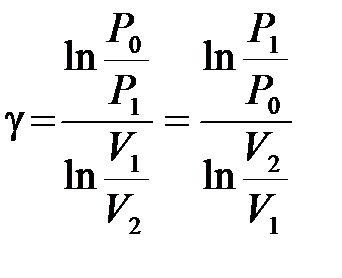 . (10.15)
. (10.15)
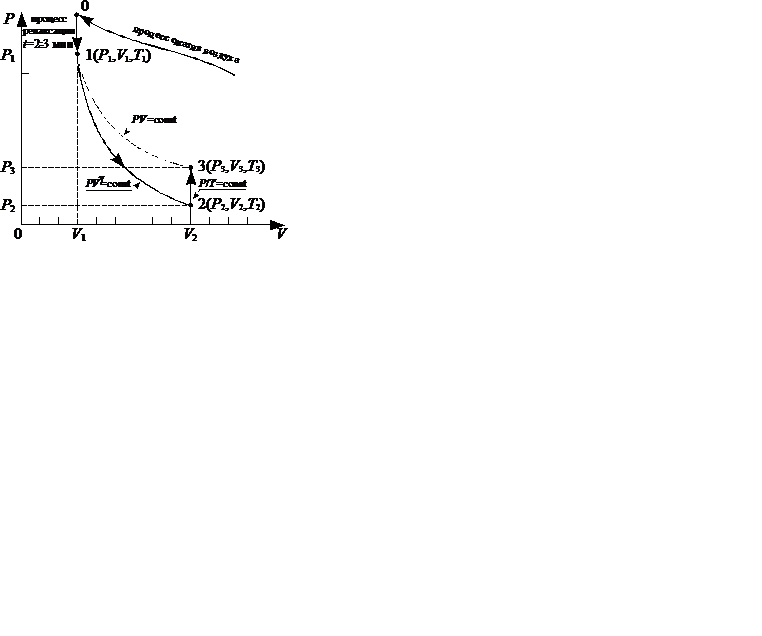
Рис.10.3
В формуле (10.15)
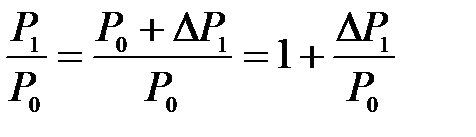 и
и 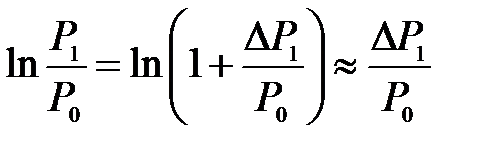 ,
,
так как
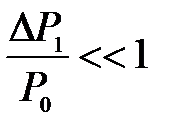 .
.
Особенностъ метода Клемана и Дезорма состоит в том, что после адиабатического процесса 1 - 2 из состояния 2 система, сохраняя постоянный объем, изохорически в течение некоторого времени переходит в равновесное состояние 3 (рис.10.3), приобретая температуру 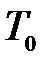 внешней среды:
внешней среды:  ,
, 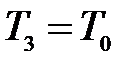 и
и 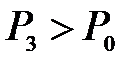 . Таким образом, состояния 1 и 3 являются изотермическими (
. Таким образом, состояния 1 и 3 являются изотермическими (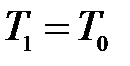 и
и 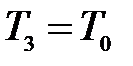 ), т.е. принадлежат некоторой теоретической изотерме (на рис.10.3 – пунктирная линия
), т.е. принадлежат некоторой теоретической изотерме (на рис.10.3 – пунктирная линия 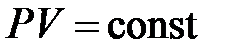 ). Поэтому для этих состояний можно записать равенство
). Поэтому для этих состояний можно записать равенство
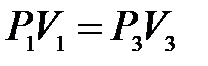
либо, учитывая, что  , равенство
, равенство
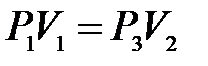 .
.
Отсюда следует, что в формуле (10.15) неизвестное отношение объемов можно заменить отношением давлений
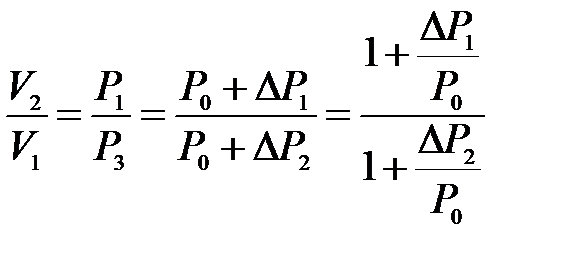 ,
,
где 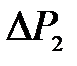 – приращение давления при изохорическом процессе. Учитывая, что
– приращение давления при изохорическом процессе. Учитывая, что  и
и 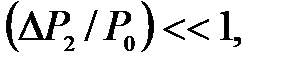 получим
получим
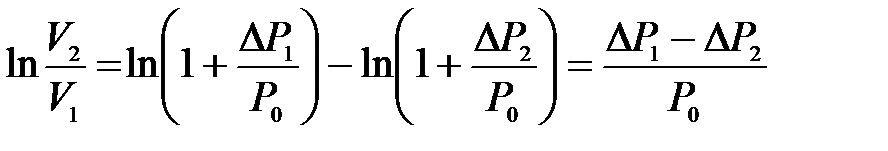 .
.
Подставляя найденные выражения для  и
и 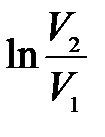 в формулу (10.15), запишем в окончательном виде соотношение, позволяющее определить показатель адиабаты по методу Клемана и Дезорма:
в формулу (10.15), запишем в окончательном виде соотношение, позволяющее определить показатель адиабаты по методу Клемана и Дезорма:
 . (10.16)
. (10.16)
Измерения с помощью формулы (10.16) являются косвенными. Однако при обработке результатов измерений их следует рассматривать как прямые, в каждом эксперименте вычисляя значение 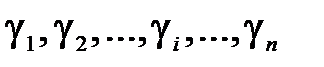 , а затем находя среднее значение
, а затем находя среднее значение 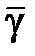 и доверительную погрешность
и доверительную погрешность 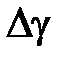 . Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (
. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (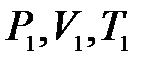 ) системы, которое образуется спонтанно из неравновесного состояния 0 (рис.10.3), в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
) системы, которое образуется спонтанно из неравновесного состояния 0 (рис.10.3), в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
Задание к работе
1. Получите допуск к выполнению работы у преподавателя.
2. Изучите метод Клемана и Дезорма, применяемый для измерения показателя адиабаты.
3. Подготовьте таблицу для измерения приращения давления 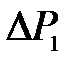 и
и 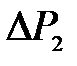 и статистической обработки результатов.
и статистической обработки результатов.
4. Откройте вентиль 6.
5. Насосом 5 малыми порциями накачайте воздух в сосуд 1, создавая давление, при котором в открытом колене манометра 4 уровень жидкости установится вблизи верхнего деления шкалы. Следите, чтобы жидкость из трубки манометра не вылилась наружу.
6. Закройте вентиль 6.
7. В течение 2-3 минут дайте системе прийти в состояние равновесия (исходное состояние 1) с температурой, равной температуре внешней среды; измерьте приращение давления 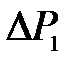 по шкале манометра 4.
по шкале манометра 4.
8. Резким нажатием клапана 3 осуществите быстрое адиабатическое расширение системы; в момент выравнивания уровней жидкости в обоих коленах манометра клапан 3 отпустите.
9. В течение 2-3 минут осуществите изохорический процесс, по окончании которого система придет в состояние равновесия 3, в котором давление  стабилизируется, а температура станет равной температуре внешней среды. Измерьте приращение давления
стабилизируется, а температура станет равной температуре внешней среды. Измерьте приращение давления 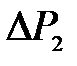 по шкале манометра 4.
по шкале манометра 4.
10. С помощью формулы (10.16) вычислите значение показателя адиабаты.
11. Проведите 10-15-кратное измерение (пункты 4-10) показателя адиабаты для воздуха, определяя приращения давления 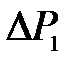 и
и 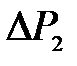 и вычисляя g по формуле (10.16).
и вычисляя g по формуле (10.16).
12. Вычислите среднее значение показателя адиабаты 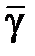 и случайную погрешность измерений
и случайную погрешность измерений 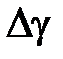 при доверительной вероятности p = 95%, считая измерения показателя адиабаты прямыми.
при доверительной вероятности p = 95%, считая измерения показателя адиабаты прямыми.
13. Считая воздух двухатомным идеальным газом, найдите для него теоретическое значение показателя адиабаты. Сравните теоретическое и экспериментально полученное значения.
Контрольные вопросы
1. Какова цель данной лабораторной работы?
2. Назовите законы идеального газа.
3. Дайте определение термодинамически изолированной системы.
4. Какие состояния системы называют равновесными?
5. Какие процессы называют равновесными и квазиравновесными?
6. Дайте определение всех изопроцессов и адиабатного процесса, напишите уравнения этих процессов, нарисуйте их графическое изображение на диаграмме состояний.
7. Охарактеризуйте изопроцессы и адиабатный процесс с точки зренияих равновесности.
8. Число степеней свободы молекулы. Чему оно равно для одно-, двух- и трехатомных молекул?
9. Дайте определение теплоемкости, удельной и молярной теплоемкостей системы. Чему равны молярные теплоемкости идеального газа при изобарическом и изохорическом процессах? Как эти теплоемкости связаны друг с другом?
10. Изложите сущность метода Клемана и Дезорма для измерения показателя адиабаты.
11. Что называется показателем адиабаты, чем он определяетсяи как связан с теплоемкостями идеального газа при изобарическом и изохорическом процессах?
11. ИЗУЧЕНИЕ ФАЗОВЫХ ПРЕВРАЩЕНИЙ ПЕРВОГО РОДА НА ПРИМЕРЕ НАГРЕВАНИЯ И ПЛАВЛЕНИЯ ОЛОВА
Дата добавления: 2015-08-17; просмотров: 150 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лабораторная работа 9 | | | Описание экспериментальной установки |