
|
Читайте также: |
Цель работы – изучение основного закона динамики вращательного движения твердого тела на примере маятника Обербека.
Описание экспериментальной установки
Маятник Обербека представляет собой крестовину, состоящую из четырёх стержней с нанесенными на них делениями, прикреплённых к барабану с осью (рис.6.1). На стержни надеваются одинаковые грузы в виде цилиндров массой  , радиусом
, радиусом  и образующей
и образующей 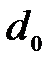 , которые могут быть закреплены на расстоянии
, которые могут быть закреплены на расстоянии  от оси вращения. На шкив радиусом
от оси вращения. На шкив радиусом 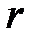 наматывается нить, к свободному концу которой прикрепляется груз массой
наматывается нить, к свободному концу которой прикрепляется груз массой  . Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Время движения груза
. Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Время движения груза  измеряется электронным секундомером, включение которого производится кнопкой «Пуск», а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние h, измеряемое вертикально закрепленной линейкой. Установка имеет электромеханическое тормозное устройство, управление которого осуществляется по сигналу фотодатчика.
измеряется электронным секундомером, включение которого производится кнопкой «Пуск», а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние h, измеряемое вертикально закрепленной линейкой. Установка имеет электромеханическое тормозное устройство, управление которого осуществляется по сигналу фотодатчика.

Рис.6.1
Методика эксперимента и вывод рабочих формул
Вращение – одна из распространенных форм движения в природе и технике. Вращаются колеса автомобилей, оси различных движущихся агрегатов, вращаются планеты вокруг своих осей и вокруг Солнца, вращаются звезды и целые галактики. Знать хорошо механику полезно и с той точки зрения, что часто механические модели используются для объяснения более сложных физических явлений в молекулярной физике, электродинамике, атомной физике и т. д. Таким образом, для дальнейшего успешного изучения физики и других дисциплин, в том числе и специальных, необходимо прочно усвоить фундаментальные законы механики и, конечно, основной закон динамики вращательного движения твердого тела.
Абсолютно твердым телом называется такое тело, расстояния между частицами которого не меняются во время движения.
При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности определенных радиусов  . Центры этих окружностей лежат на оси вращения (рис. 6.2).
. Центры этих окружностей лежат на оси вращения (рис. 6.2).
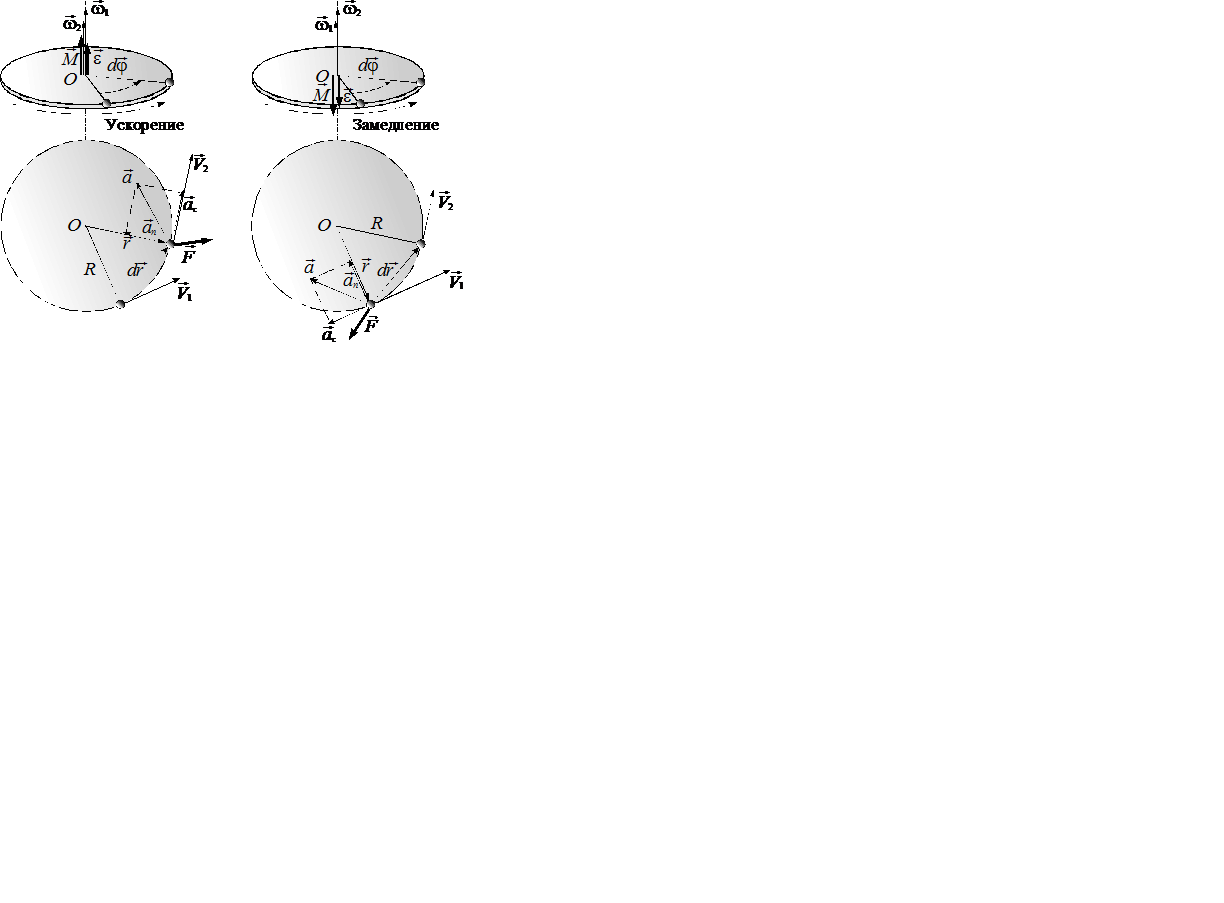
Рис.6.2
Для характеристики вращательного движения твердого тела вводят понятие угловой скорости.
Угловая скорость – это векторная физическая величина, характеризующая быстроту вращательного движения твердого тела:
 . (6.1)
. (6.1)
Единицей измерения угловой скорости в системе СИ является  .
.
Вектор  называется вектором элементарного углового перемещения. Длина его численно равна углу поворота
называется вектором элементарного углового перемещения. Длина его численно равна углу поворота  , выраженного в радианах, а направление совпадает с перпендикуляром к плоскости, в которой происходит этот поворот: если рукоятку правого винта вращать по направлению движения точки, то поступательное движение самого винта совпадает с направлением
, выраженного в радианах, а направление совпадает с перпендикуляром к плоскости, в которой происходит этот поворот: если рукоятку правого винта вращать по направлению движения точки, то поступательное движение самого винта совпадает с направлением  (правило буравчика).
(правило буравчика).
Как следует из (6.1) угловая скорость соноправлена с вектором элементарного углового перемещения (  ).
).
Вектор  может изменяться с течением времени как за счет изменения величины скорости вращения тела вокруг оси, так и за счет изменения направления вращения.
может изменяться с течением времени как за счет изменения величины скорости вращения тела вокруг оси, так и за счет изменения направления вращения.
Угловое ускорение – это векторная физическая величина, характеризующая быстроту изменения угловой скорости:
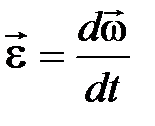 . (6.2)
. (6.2)
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости  , т.е. при ускоренном вектор
, т.е. при ускоренном вектор  сонаправлен с вектором
сонаправлен с вектором  (
( ), при замедленном движении вектор
), при замедленном движении вектор  направлен противоположно
направлен противоположно  (
( ) (см. рис.6.2). Единицей измерения углового ускорения в системе СИ является радиан на секунду в квадрате
) (см. рис.6.2). Единицей измерения углового ускорения в системе СИ является радиан на секунду в квадрате  .
.
Вращение можно также характеризовать линейной скоростью  , линейным ускорением
, линейным ускорением  , а также нормальным
, а также нормальным  и тангенциальным
и тангенциальным  ускорением (см. гл.1).
ускорением (см. гл.1).
Мерой действия, вызывающего вращение твердого тела, является момент силы:
 , (6.3)
, (6.3)
где 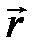 – радиус-вектор точки приложения силы;
– радиус-вектор точки приложения силы;  – сила, приложенная к телу;
– сила, приложенная к телу;  – угол между направлениями векторов
– угол между направлениями векторов 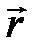 и
и  . Момент силы направлен вдоль оси вращения твердого тела.
. Момент силы направлен вдоль оси вращения твердого тела.
Следует помнить, что одна масса не является мерой инертности при вращательном движении твердого тела, так как при одной и той же массе инертность вращающихся тел может быть разной из-за различного ее распределения относительно оси вращения.
Мерой инертности при вращательном движении твердого тела является момент инерции  – скаляр, определяемый как
– скаляр, определяемый как
 ,
,
или для однородных тел
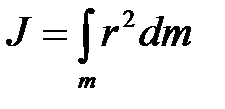 , (6.4)
, (6.4)
где  ,
,  – масса малого или элементарного объема твердого тела;
– масса малого или элементарного объема твердого тела;  – расстояние от этого объема до оси вращения.
– расстояние от этого объема до оси вращения.
Момент инерции сложного тела равен сумме моментов инерции его составных частей.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно другой параллельной оси определяется теоремой Штейнера: момент инерции тела  относительно любой оси вращения равен моменту его инерции
относительно любой оси вращения равен моменту его инерции  относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы
относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы  на квадрат расстояния
на квадрат расстояния  между осями:
между осями:
 . (6.5)
. (6.5)
Величина момента инерции тела зависит от массы тела и её распределения относительно оси вращения.
Основной закон динамики вращательного движения твердого тела – геометрическая сумма моментов внешних сил  , действующих на тело, равна скорости изменения момента импульса этого тела
, действующих на тело, равна скорости изменения момента импульса этого тела
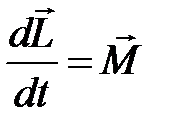 , (6.6)
, (6.6)
где в случае тела, симметричного относительно неподвижной оси вращения,
 (6.7)
(6.7)
есть момент импульса твердого тела, совпадающий по направлению с вектором угловой скорости  .
.
При 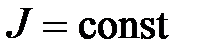 с учетом (6.7) закон (6.6) имеет вид
с учетом (6.7) закон (6.6) имеет вид
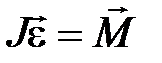 , (6.8)
, (6.8)
где угловое ускорение  .
.
Экспериментальная проверка выполнения закона (6.8) состоит в том, чтобы показать:
1) пропорциональность углового ускорения  моменту силы
моменту силы  , т.е.
, т.е. 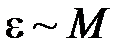 , которое проверяется при неизменном моменте инерции
, которое проверяется при неизменном моменте инерции 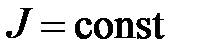 для двух разных моментов сил
для двух разных моментов сил  и
и  :
:
 . (6.9)
. (6.9)
2) обратную пропорциональность углового ускорения  моменту инерции
моменту инерции  , т.е.
, т.е.  , проверяется при неизменном моменте силы
, проверяется при неизменном моменте силы  для двух разных моментов инерции
для двух разных моментов инерции  и
и  :
:
 . (6.10)
. (6.10)
При 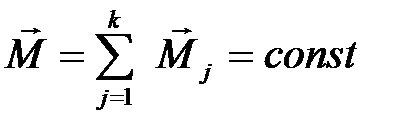 в течение времени
в течение времени  формула (6.6) преобразуется в формулу
формула (6.6) преобразуется в формулу  . Тогда для двух разных опытов можно проверить справедливость отношения
. Тогда для двух разных опытов можно проверить справедливость отношения
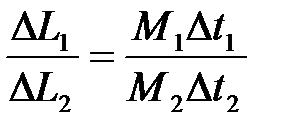 ,
,
или
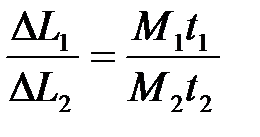 , (6.11)
, (6.11)
если отсчет времени производится от  .
.
Величины  и
и  – соответствующие изменения моментов импульсов твердого тела при начальной угловой скорости
– соответствующие изменения моментов импульсов твердого тела при начальной угловой скорости  .
.
Для более полной и детальной информации следует обратиться к литературе, например [1-4].
На рис.6.1 показаны силы, действующие на различные элементы установки. Так, на груз  действуют:
действуют:  – сила тяжести;
– сила тяжести;  – сила реакции нити. На нить:
– сила реакции нити. На нить:  – сила со стороны груза
– сила со стороны груза  ,
, 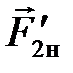 – сила со стороны блока;
– сила со стороны блока;  – сила тяжести, если нить весомая. На блок:
– сила тяжести, если нить весомая. На блок:  – сила со стороны нити;
– сила со стороны нити;  – сила реакции со стороны оси;
– сила реакции со стороны оси;  – сила тяжести блока, крестовины и четырех грузов массой
– сила тяжести блока, крестовины и четырех грузов массой  (последние две на рисунке не показаны). Поступательное движение груза
(последние две на рисунке не показаны). Поступательное движение груза 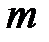 , нити
, нити 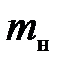 и вращательное движение маятника можно описать с помощью второго и третьего законов Ньютона и основного закона динамики вращательного движения твердого тела (6.8):
и вращательное движение маятника можно описать с помощью второго и третьего законов Ньютона и основного закона динамики вращательного движения твердого тела (6.8):
 ,
,
 ,
,
 , (6.12)
, (6.12)
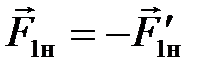 ,
,  ,
,
где  – момент сил трения (тормозящий момент);
– момент сил трения (тормозящий момент);  ,
, 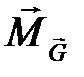 ,
,  – моменты сил
– моменты сил  ,
, 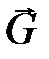 ,
,  соответственно;
соответственно;  – момент инерции крестовины с грузами
– момент инерции крестовины с грузами  (
( );
);  ,
,  – масса и ускорение нити.
– масса и ускорение нити.
Полагаем, что нить нерастяжима, тогда ее ускорение  равно ускорению
равно ускорению  груза
груза 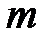 . Нить не скользит по блоку. Это означает, что
. Нить не скользит по блоку. Это означает, что  равно тангенциальному ускорению
равно тангенциальному ускорению  точек блока на его боковой поверхности:
точек блока на его боковой поверхности:  . При этом условии угловое ускорение ε можно найти из равенства
. При этом условии угловое ускорение ε можно найти из равенства
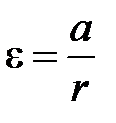 . (6.13)
. (6.13)
При условии невесомости нити  из второго и четвертого уравнений (6.12) следует, что
из второго и четвертого уравнений (6.12) следует, что  . Моменты сил
. Моменты сил  и
и 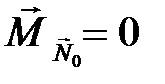 , так как силы пересекают ось вращения. Момент силы
, так как силы пересекают ось вращения. Момент силы  , согласно (6.3), равен
, согласно (6.3), равен  . Поскольку
. Поскольку  (см. рис.6.1),
(см. рис.6.1),
 . (6.14)
. (6.14)
Полагая в (6.12)  и учитывая (6.13) и (6.14), из (6.12) в проекциях на оси
и учитывая (6.13) и (6.14), из (6.12) в проекциях на оси  и
и  получим
получим
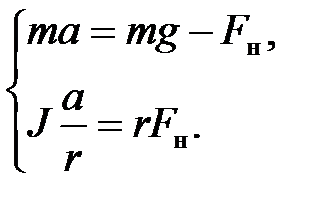 (6.15)
(6.15)
Из (6.15) найдем момент силы  :
:
 (6.16)
(6.16)
и момент инерции вращающейся части установки:
 . (6.17)
. (6.17)
Из уравнения (6.16) видно, что момент силы в рассматриваемой системе тел зависит от массы груза  и радиуса блока. От этих же факторов зависит и ускорение
и радиуса блока. От этих же факторов зависит и ускорение  . Движение груза
. Движение груза  можно считать равноускоренным, так как сила
можно считать равноускоренным, так как сила  при постоянстве перечисленных ранее факторов не меняется. Тогда ускорение груза
при постоянстве перечисленных ранее факторов не меняется. Тогда ускорение груза  при его начальной скорости
при его начальной скорости  определится по формуле
определится по формуле
 , (6.18)
, (6.18)
где  – высота, с которой опускается груз;
– высота, с которой опускается груз; 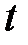 – время его движения.
– время его движения.
Поскольку крестовина с грузами  начинает вращение из состояния покоя, ее угловую скорость в конечный момент движения груза
начинает вращение из состояния покоя, ее угловую скорость в конечный момент движения груза 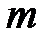 можно вычислить по формуле
можно вычислить по формуле
 , (6.19)
, (6.19)
а изменение ее момента импульса  за это время
за это время
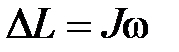 . (6.20)
. (6.20)
В результате равенство (6.11) примет вид
 . (6.21)
. (6.21)
Измерив высоту  движения груза
движения груза  , время
, время  его движения и радиус
его движения и радиус 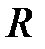 блока, можно по формулам (6.18), (6.13), (6.16), (6.17), (6.19) вычислить
блока, можно по формулам (6.18), (6.13), (6.16), (6.17), (6.19) вычислить  ,
, 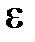 ,
,  ,
,  ,
, 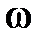 .
.
Дата добавления: 2015-08-17; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание к работе | | | Задание к работе |