Лабораторная работа 1

Цель работы – изучение движения тела, брошенного под углом к горизонту; экспериментальная проверка теоретического выражения для дальности полета тела.

Описание экспериментальной установки

Экспериментальная установка представляет собой пружинный пистолет, закрепленный на высоте над узкой доской вблизи ее конца. Угол наклона ствола пистолета a может изменяться. В наборе имеется несколько пуль с различной массой m. Поверхность доски и передняя часть пули покрыты лентой-липой, что позволяет предотвратить отскок пули при падении, а также зафиксировать положение пули для измерения дальности ее полета. Эти измерения проводятся с помощью закрепленной вдоль доски линейки.

Методика эксперимента и вывод рабочих формул

Кинематика – раздел механики, изучающий движение тел независимо от причин, обусловливающих это движение. Во многих случаях кинематика имеет дело с материальной точкой – телом, размерами которого в условиях данной задачи можно пренебречь.

Положение материальной точки в пространстве определяется заданием трех ее координат, например, трех декартовых координат , и . Совокупность трех величин x, y и z образует радиус-вектор, направленный из начала координат в точку, где находится частица (рис.1.1). Модуль этого вектора равен:

. (1.1)

Рис.1.1

Если точка движется, то ее положение относительно системы отсчета меняется со временем: . Геометрическое место точек концов радиуса-вектора представляет собой траекторию движения материальной точки. Для характеристики движения материальной точки вводится понятие скорости.

Скорость – это векторная физическая величина, характеризующая направление и быстроту движения материальной точки:

. (1.2)

Скорость направлена по касательной к траектории движения и имеет размерность .

Если при движении материальной точки ее скорость меняется, то для описания этого изменения вводится понятие ускорения.

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости, как по величине, так и по направлению:

. (1.3)

Как следует из (1.3) ускорение измеряется в .

Наиболее простой вид движения – это прямолинейное движение материальной точки.

Движение, при котором материальная точка за любые равные промежутки времени совершает равные перемещения, называется равномерным прямолинейным движением. Для данного типа движения справедливо:

,

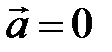, (1.4)

.

Движение, при котором скорость материальной точки за любые равные промежутки времени изменяется на одинаковую величину, называется равнопеременным прямолинейным движением. Для данного типа движения справедливо:

,

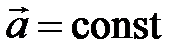, (1.5)

.

Если , то движение называют равноускоренным, в противном случае, когда , – равнозамедленным.

Вектор ускорения при криволинейном движении тела часто представляют в виде суммы двух составляющих (рис.1.2):

, (1.6)

где 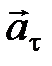− тангенциальное ускорение, направленное по касательной к траектории движения; − нормальное ускорение, направленное по нормали к траектории (перпендикулярно касательной) к центру её кривизны.

Рис.1.2

Из рисунка видно, что модуль полного ускорения равен

. (1.7)

Тангенциальное ускорение характеризует быстроту изменения скорости по величине, следовательно,

. (1.8)

Нормальное ускорение определяет быстроту изменения скорости по направлению и численно определяется как

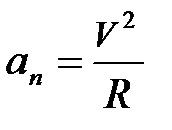, (1.9)

где R − радиус кривизны траектории в данной точке.

Для более полной и детальной информации следует обратиться к литературе, например [1-4].

Тело (пуля), брошенное под углом a к горизонту (рис.1.3), движется под действием силы тяжести. Если другими силами (например, сопротивлением воздуха) можно пренебречь, то движение называют свободным падением. Ускорение при этом называют ускорением свободного падения . Оно направлено вертикально вниз и в условиях опыта может считаться постоянным по модулю.

Рис.1.3

Движение тела можно описать следующими векторными кинематическими уравнениями:

, (1.10)

, (1.11)

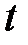где – вектор скорости пули в момент времени ; – вектор скорости пули при (начальная скорость); – радиус-вектор, определяющий местоположение пули в момент времени t относительно начала координат; – радиус-вектор в момент времени .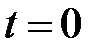

В проекциях на ось X, направленную горизонтально в сторону полета пули, и ось Y, направленную вертикально вверх (рис.1.3), уравнения (1.10) и (1.11) имеют вид:

; (1.12)

; (1.13)

; (1.14)

. (1.15)

Таким образом, это сложное движение материальной точки (пули) можно рассматривать как результат сложения двух движений: равномерного прямолинейного движения по оси и равнопеременного прямолинейного движения по оси .

Скорость пули сразу после выстрела можно определить, стреляя первоначально в горизонтальном направлении (). Из (1.14) и (1.15) при этом получим:

. (1.16)

где 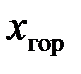– дальность полета пули.

Таким образом, произведя выстрел в горизонтальном направлении с высоты , и измерив дальность полета пули , по формуле (1.16) можно вычислить ее начальную скорость . Эта скорость определяется потенциальной энергией сжатой пружины пистолета, она практически не зависит от угла a.

Теперь рассмотрим полет пули, пущенной под углом a к горизонту с высоты . В точке падения координата . Используя (1.14) и (1.15), обозначив дальность полета пули , получим формулу для расчета этой величины:

, (1.17)

где 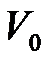определяется по формуле (1.16).

Задание к работе

1. Получите допуск к выполнению лабораторной работы у преподавателя.

2. Установите пружинный пистолет горизонтально. Определите высоту , на которой находится пуля. Соблюдая правила техники безопасности, зарядите пистолет, закрепив в стволе одну из пуль.

3. Нажав спусковую кнопку, произведите выстрел. Измерьте дальность полета . Запишите полученные результаты.

4. Повторите опыт пятикратно. Рассчитайте среднюю дальность полета и определите доверительную погрешность измерения .

5. Рассчитайте значение начальной скорости пули , используя формулу (1.16). Определите погрешность косвенных измерений начальной скорости.

6. Установите пружинный пистолет под углом к горизонту. Запишите значение этого угла.

7. Зарядите пистолет пулей, для которой проведен опыт пункта 2. Произведите выстрел. Измерьте и запишите дальность полета этой пули при заданном угле .

8. Повторите опыт пятикратно. Проведите статистическую обработку полученных результатов: определите среднюю дальность полета 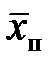и доверительную погрешность измерения .

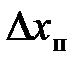9. Получите расчетное значение дальности полета пули по формуле (1.17). Сравните его с полученным в опыте.

10. Повторите пункты 4-6 для других (по указанию преподавателя) углов .

11. Повторите пункты 1-6 для пуль с другими (по указанию преподавателя) массами.

Контрольные вопросы

1. Какова цель данной лабораторной работы?

2. Какими характеристиками описывается движения материальной точки?

3. Какое движение называется равномерным прямолинейным? равнопеременным прямолинейным?

4. Получите векторные кинематические уравнения (1.4) и (1.5).

5. Какое движение тела называется «свободным падением»? С каким ускорением оно происходит?

6. Как можно определить скорость пули сразу после выстрела. От чего она зависит?

7. Зависит ли начальная скорость пули от ее массы? Какой характер имеет эта зависимость?

8. Получите формулу для определения дальности полета пули, пущенной под углом к горизонту с высоты . Начальная скорость пули равна .

9. Используя формулы (1.14) и (1.15), получите уравнение траектории пули. Определите координаты ее вершины. Чему равна и как направлена скорость пули в верхней точке траектории?

10. Определите при каком угле дальность полета пули будет максимальной. Какова при этом будет высота подъема пули?

2. Определение коэффициента трения скольжениЯ

Лабораторная работа 2

Цель работы – изучение законов сухого (внешнего) трения, экспериментальное определение коэффициента трения скольжения.

Описание экспериментальной установки

Установка представляет собой наклонную плоскость 1, которую с помощью винта 2 можно устанавливать под разными углами a к горизонту (рис. 2.1). Угол a измеряется с помощью шкалы 3. На плоскость может быть помещен брусок 4 массой m. Предусмотрено использование двух брусков разной массы. Каждый брусок состоит из двух частей, изготовленных из различных материалов: дерево-дюраль и дерево-сталь. Бруски закрепляются в верхней точке наклонной плоскости с помощью электромагнита 5, управление которым осуществляется с помощью электронного секундомера СЭ1. Пройденное бруском расстояние измеряется линейкой 6, закрепленной вдоль плоскости. Время соскальзывания бруска измеряется автоматически с помощью датчика 7, выключающего секундомер в момент касания бруском финишной точки.

Рис.2.1

Методика эксперимента и вывод рабочих формул

Динамика – раздел механики, изучающий движения тел в связи с теми причинами, которые обусловливают тот или иной характер движения.

В основе так называемой классической или ньютоновской механики лежат три закона, сформулированные И. Ньютоном в 1687 г. Законы Ньютона возникли в результате обобщения большого количества опытных фактов. Классическая механика является механикой тел больших (по сравнению с массой атомов) масс, движущихся с малыми (по сравнению со скоростью света) скоростями.

Первый закон Ньютона: существуют такие системы отсчета, относительно которых, всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока на него не действуют внешние силы или это действие скомпенсировано.

Таким образом, тело изменяет свою скорость, когда на него действуют другие тела. Если воздействия со стороны других тел отсутствуют, то скорость тела остается неизменной .

Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Инерциальной системой отсчета является такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно другой инерциальной системы. Первый закон Ньютона называют иногда законом инерции.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью тела. Мерой инертности тел является масса. Масса тела − физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. Инертная и гравитационная массы равны друг другу с точностью, не меньшей 10^-12 их значения.

Чтобы описать воздействия, упоминаемые в первом законе Ньютона, вводится понятие силы. Сила − это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение (динамическое проявление силы) или изменяет свою форму или размеры (статическое проявление силы). Единица силы в системе СИ − Ньютон (Н).

Второй закон Ньютона (основной закон динамики поступательного движения): ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело и вызвавшей данное ускорение, и обратно пропорционально массе тела:

, (2.1)

где − векторная сумма всех сил, действующих на тело. Из (2.1) следует, что ускорение всегда сонаправлено с силой (равнодействующей), вызвавшей данное ускорение ().

Таким образом, второй закон Ньютона устанавливает связь между мерой взаимодействия (силой ), мерой инертности тел (массой 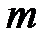) и ускорением .

Учитывая, что в классической механике масса материальной точки (тела) есть величина постоянная, то второй закон Ньютона можно записать в виде

.

Векторная величина , численно равная произведению массы тела на его скорость и имеющая направление скорости, называется импульсом (количеством движения) этого тела.

Выражение

(2.2)

является более общей формулировкой второго закона Ньютона: скорость изменения импульса тела равна действующей на тело силе.

Взаимодействие между телами определяется третьим законом Ньютона: тела действуют друг на друга с силами равными по величине и противоположными по направлению, причем приложены эти силы к разным телам:

, (2.3)

где – сила, действующая на первое тело со стороны второго; – сила, действующая на второе тело со стороны первого.

Из третьего закона Ньютона следует:

1) силы в природе возникают попарно;

2) силы взаимодействия не могут компенсировать друг друга, так как приложены к разным телам.

В современной физике различают четыре вида взаимодействий:

1) гравитационное (или взаимодействие, обусловленное всемирным тяготением);

2) электромагнитное (осуществляемое через электрические и магнитные поля);

3) сильное или ядерное (обеспечивающее связь частиц в атомном ядре);

4) слабое (ответственное за многие распады элементарных частиц).

В рамках классической механики имеют дело с гравитационными и электромагнитными силами, которые являются фундаментальными, т. е. их нельзя свести к другим, более простым, силам, а также с упругими силами и силами трения, которые определяются характером взаимодействия между молекулами вещества. Для этих сил можно получить лишь приближенные эмпирические формулы.

Для более полной и детальной информации следует обратиться к литературе, например [1-4].

При соскальзывании бруска с наклонной плоскости на него действует несколько сил: сила тяжести , сила нормальной реакции опоры и сила трения скольжения (рис. 2.2). Ускорение бруска постоянно и направлено вдоль плоскости вниз.

Выберем направление координатной оси X вдоль плоскости вниз, а координатной оси Y перпендикулярно плоскости вверх. Запишем уравнение динамики поступательного движения бруска (второй закон Ньютона) в проекциях на эти оси:

OX: ; (2.4)

OY: . (2.5)

Рис.2.2

Учтем, что сила трения скольжения равна

, (2.6)

где – коэффициент трения скольжения.

Решая систему уравнений (2.4)-(2.6), получаем

. (2.7)

Величину ускорения можно найти, измерив пройденный бруском путь S и соответствующее время :

. (2.8)

Формула (2.8) получена при нулевом значении начальной скорости, что соответствует условиям опыта. Подставляя (2.8) в (2.7), получаем рабочую формулу для определения коэффициента трения скольжения:

. (2.9)

Задание к работе

1. Получите допуск к выполнению лабораторной работы у преподавателя.

2. Ослабив винт 2 (рис. 2.1), установите плоскость под углом 25° к горизонту, электромагнит при этом должен находиться в нижней части плоскости. Закрепите плоскость в таком положении, зажав винт 2.

3. Включите секундомер СЭ-1. Убедитесь, что он находится в режиме 1.

4. Поместите брусок с большей массой (сталь-дерево) на наклонную плоскость в положении деревом вниз, прижмите торец бруска, на который наклеена металлическая пластина, к электромагниту. Убедитесь, что брусок удерживается в этом положении.

5. Нажмите кнопку «Пуск» секундомера. При этом происходит одновременное отключение электромагнита и включение секундомера. Выключение секундомера происходит автоматически в момент удара бруска по финишному датчику.

6. Занесите время соскальзывания бруска t, пройденный бруском путь S в табл. 2.1.

7. Вычислите коэффициент трения скольжения по формуле (2.7). Результат занесите в табл. 2.1.

8. Повторите опыт пятикратно. Проведите статистическую обработку полученных результатов, определите погрешность измерений коэффициента трения скольжения. Запишите результат в виде

Таблица 2.1

№ п/п	t, с	S, м

9. Повторите пункты 3-7, повернув брусок в положение сталью вниз.

10. Повторите пункты 3-8 для других (по указанию преподавателя) углов .

11. Повторите пункты 3-9 для второго бруска.

12. Сравните полученные в опыте значения коэффициентов трения скольжения с табличными.

Контрольные вопросы

1. Какова цель данной лабораторной работы?

2. Какое трение называется сухим (внешним)? Чем оно обусловлено? Какие виды сухого трения Вы знаете?

3. Как определить направление силы трения покоя и силы трения скольжения?

4. Сформулируйте законы сухого (внешнего) трения.

5. От чего зависит коэффициент трения скольжения?

6. Докажите, что движение бруска по наклонной плоскости является равноускоренным.

7. Получите рабочую формулу для определения коэффициента трения скольжения.

3. ИЗМЕРЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Дата добавления: 2015-08-17