
|
Читайте также: |
Цель работы – ознакомление с элементами теории механического удара и экспериментальное определение времени удара  , средней силы удара
, средней силы удара 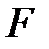 , коэффициент восстановления
, коэффициент восстановления 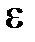 .
.
Описание экспериментальной установки
Экспериментальная установка состоит из стального шарика  , подвешенного на проводящих нитях и неподвижного тела
, подвешенного на проводящих нитях и неподвижного тела  большой массы
большой массы  , с которой шарик соударяется (рис. 5.1). Начальный угол отклонения подвеса шара от вертикального положения
, с которой шарик соударяется (рис. 5.1). Начальный угол отклонения подвеса шара от вертикального положения  определяется с помощью шкалы. Также по шкале определяется максимальный угол отклонения шара после удара.
определяется с помощью шкалы. Также по шкале определяется максимальный угол отклонения шара после удара.
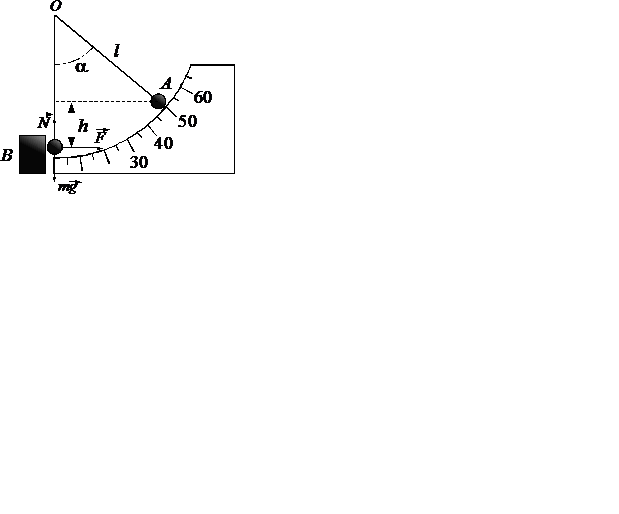
Рис.5.1
Методика эксперимента и вывод рабочих формул
Ударом называется изменение состояния движения тела вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменение формы (деформацию).
Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел за короткое время преобразуется в энергию упругой деформации и в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.
Процесс удара можно разделить на две фазы. В течение первой фазы происходит сближение тел. При этом кинетическая энергия системы тел уменьшается, относительная скорость убывает до нуля. Вслед за этим наступает вторая фаза удара: тела начинают удаляться друг от друга, восстанавливая свою форму, а кинетическая энергия и относительная скорость их возрастает. Когда тела отдаляются. Процесс удара заканчивается.
Наблюдения показывают, что относительная скорость после удара не достигает своего прежнего численного значения. Это объясняется тем, что на практике мы никогда не имеем дело с идеально упругими деформациями тел.
Пусть на плоскую поверхность массивной пластины падает шар с некоторой скоростью  и отскакивает от неё со скоростью
и отскакивает от неё со скоростью  (см. рис. 5.2).
(см. рис. 5.2).

Рис.5.2
Обозначим:  ,
,  ,
,  ,
,  – нормальные и тангенциальные составляющие скоростей
– нормальные и тангенциальные составляющие скоростей  и
и  , а
, а  и
и  соответственно углы падения и отражения. В идеальном случае, при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны
соответственно углы падения и отражения. В идеальном случае, при абсолютно упругом ударе, нормальные составляющие скоростей падения и отражения и их касательные составляющие были бы равны  ,
,  .
.  Это означало бы, что скорость шара до удара равна его скорости после удара
Это означало бы, что скорость шара до удара равна его скорости после удара  а также угол падения равен углу отражения
а также угол падения равен углу отражения  . В условиях реального удара всегда происходит потеря механической энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются:
. В условиях реального удара всегда происходит потеря механической энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются:  ,
, 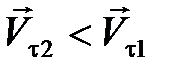 . Отношение численного значения нормальной составляющей относительной скорости после удара к её величине до удара есть физическая характеристика, зависящая от природ сталкивающихся тел
. Отношение численного значения нормальной составляющей относительной скорости после удара к её величине до удара есть физическая характеристика, зависящая от природ сталкивающихся тел 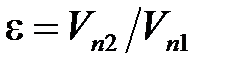 .
.
Эту характеристику  называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.
называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.
1. Вывод формул для косвенных измерений скорости шарика до и после удара, силы удара и коэффициента восстановления
В момент удара на шар массой 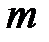 действует сила тяжести со стороны Земли
действует сила тяжести со стороны Земли  , сила реакции со стороны нити
, сила реакции со стороны нити  , средняя сила удара
, средняя сила удара  со стороны тела
со стороны тела  . На основании теоремы об изменении импульса материальной точки
. На основании теоремы об изменении импульса материальной точки
 , (5.1)
, (5.1)
где  ,
,  – векторы скоростей шара до и после удара;
– векторы скоростей шара до и после удара; 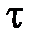 – длительность удара.
– длительность удара.
После проектирования уравнения (5.1) на горизонтальную ось определим среднюю силу удара:
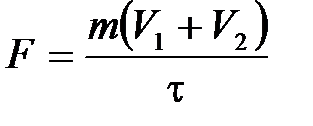 . (5.2)
. (5.2)
Скорости шарика  и
и  определяются на основании закона сохранения и превращения энергии для системы тел «шарик-плита». Поскольку внешняя сила
определяются на основании закона сохранения и превращения энергии для системы тел «шарик-плита». Поскольку внешняя сила  перпендикулярна перемещению и нить нерастяжима, то эта сила работу не совершает. Внешняя сила
перпендикулярна перемещению и нить нерастяжима, то эта сила работу не совершает. Внешняя сила  – потенциальна и ее работа при движении шарика от начального положения до момента соударения с плитой равна
– потенциальна и ее работа при движении шарика от начального положения до момента соударения с плитой равна  . Уравнение баланса энергии можно записать в виде:
. Уравнение баланса энергии можно записать в виде:
 . (5.3)
. (5.3)
Из рис. 5.1 следует, что
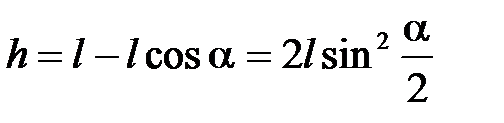 . (5.4)
. (5.4)
Тогда из уравнения (5.3) с учетом (5.4) получим значение начальной 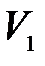 , и конечной
, и конечной  скоростей шарика:
скоростей шарика:
 , (5.5)
, (5.5)
где  и
и  – углы отклонения шара
– углы отклонения шара  до и после соударения.
до и после соударения.
Определив скорости шарика до удара  и после удара
и после удара  , можно определить коэффициент восстановления:
, можно определить коэффициент восстановления:
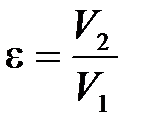 . (5.6)
. (5.6)
Для более полной и детальной информации следует обратиться к литературе, например [1-4].
2. Вывод формул для расчета погрешностей косвенных измерений
В работе определяют скорости шарика до удара  и после удара
и после удара  о металлическую плитку, время удара
о металлическую плитку, время удара 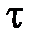 , среднюю силу удара
, среднюю силу удара  , коэффициент восстановления
, коэффициент восстановления 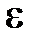 для различных начальных углов
для различных начальных углов  .
.
Исходными данными к работе являются
1. Длина нити 
 ,
,  ,
,
2. Масса шарика 
 ,
, 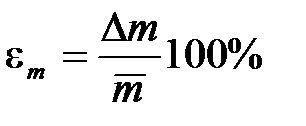 ,
,
3. Ускорение свободного падения 
 ,
, 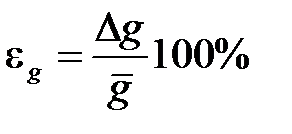 .
.
Приборные погрешности берутся равными:
1. Для цифрового измерителя времени  ,
,
2. Для шкалы отсчёта углов  .
.
Для каждого заданного угла  измеряем
измеряем  раз угол
раз угол 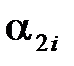 отскока шарика после удара и
отскока шарика после удара и 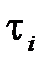 – время удара. После предварительного исследования результатов опыта на промахи (см. (12.3) гл.12) находим среднее выборочное значение:
– время удара. После предварительного исследования результатов опыта на промахи (см. (12.3) гл.12) находим среднее выборочное значение:
 ,
,
 .
.
Затем по формуле (5.5), (5.2) и (5.6) находим значение скорости до и после удара, среднюю силу удара и коэффициент восстановления:
 ,
,
 ,
,
 ,
,
 .
.
Выбираем общую для всех результатов доверительную вероятность  и для неё находим коэффициенты Стьюдента
и для неё находим коэффициенты Стьюдента  и
и  по табл. 12.3 (см. гл. 12).
по табл. 12.3 (см. гл. 12).
Погрешность измерения начального угла отклонения 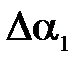 берем равной
берем равной  . Тогда относительную погрешность измерения угла
. Тогда относительную погрешность измерения угла 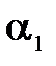 можно определить
можно определить
 .
.
Погрешность измерения начального угла отскока  определяем как погрешность многократных измерений. Для этого по формуле 12.8 (см. гл. 12) находим среднее квадратичное отклонение
определяем как погрешность многократных измерений. Для этого по формуле 12.8 (см. гл. 12) находим среднее квадратичное отклонение
 ,
,
а затем по (12.9) (см. гл. 12) определяем абсолютную погрешность  :
:
 .
.
C округлением результата можно записать
 ,
,  ,
,  .
.
Аналогично вычисляют погрешности времени удара:
 ,
,
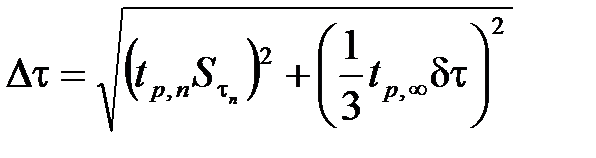 ,
,
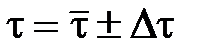 ,
,  ,
,  .
.
Расчёт погрешностей косвенных значений производится согласно гл.12.
В формулу (5.5) величины  ,
,  ,
, 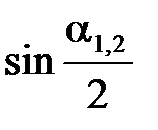 входят как сомножители, поэтому удобно воспользоваться вторым способом метода, основанного на применении формулы полного дифференциала. Логарифмируем выражение для скорости
входят как сомножители, поэтому удобно воспользоваться вторым способом метода, основанного на применении формулы полного дифференциала. Логарифмируем выражение для скорости  :
:
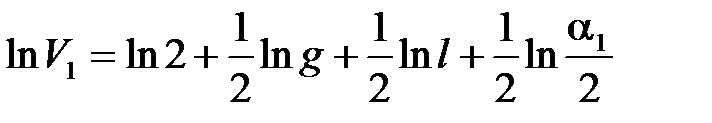 .
.
Берем частные производные по  ,
,  ,
,  и подставляем в формулу (12.17) гл. 12. После несложных математических преобразований получаем
и подставляем в формулу (12.17) гл. 12. После несложных математических преобразований получаем
 .
.
где  выражено в радианах, а
выражено в радианах, а 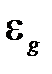 ,
,  уже найдены ранее. Находим абсолютную погрешность
уже найдены ранее. Находим абсолютную погрешность
 ,
,
и записываем результат
 ,
,  ,
,  .
.
Аналогично находим погрешности скорости 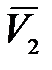 :
:
 ,
,
где  выражено в радианах, определяем
выражено в радианах, определяем  и записываем результат
и записываем результат
 ,
,  ,
,  .
.
Далее исходя из формул (5.6) и (5.2) аналогично вычисляем погрешность коэффициента восстановления
 ,
,
где 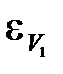 и
и  – уже найдены ранее,
– уже найдены ранее,  ,
,
 ,
, 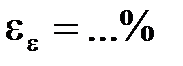 ,
,  ;
;
и средней силы удара
 ,
,
где 

 уже найдены, а
уже найдены, а  определяем следующим образом:
определяем следующим образом:
 ,
,
где  , а
, а  и
и 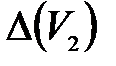 уже найдены.
уже найдены.
Далее находим абсолютную погрешность
 ,
,
и записываем результат
 ,
, 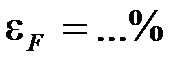 ,
,  .
.
Такую погрешность обработки экспериментальных данных следует повторить для различных углов  (по заданию преподавателя)
(по заданию преподавателя)
Дата добавления: 2015-08-17; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание к работе | | | Задание к работе |