Лабораторная работа 3

Цель работы – ознакомление с методикой определения скорости полета пули с помощью баллистического маятника.

Описание экспериментальной установки

Баллистический маятник представляет собой массивный цилиндр M, заполненный пластилином. В цилиндр в горизонтальном направлении производят выстрел пулей массы 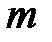из пружинного пистолета , неподвижно закрепленного вблизи маятника (рис. 3.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное горизонтальное отклонение маятника от его положения равновесия фиксируется механизмом .

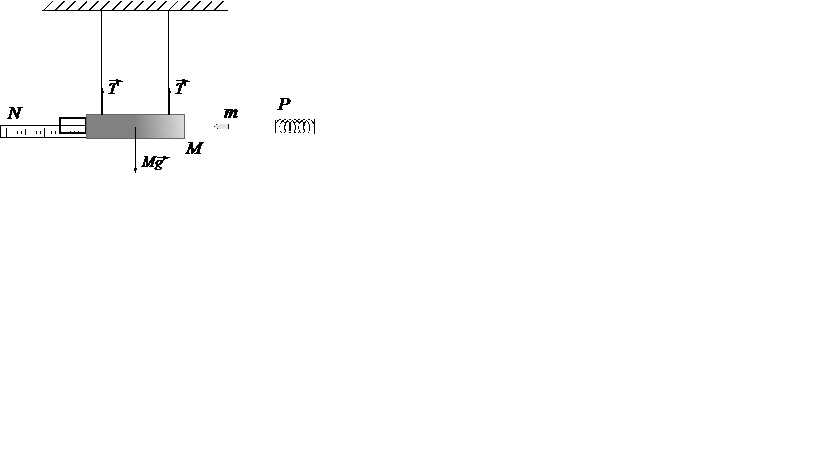
Рис.3.1

Методика эксперимента и вывод рабочих формул

Энергия является универсальной количественной мерой движения и взаимодействия всех видов материи. С различными формами движения материи связывают различные виды энергии: механическую, тепловую, электромагнитную, ядерную и др.

В одних процессах форма движения материи и, соответственно, форма энергии не меняются (например, от горячего тела тепло передается холодному), в других – одна форма движения (соответственно, форма энергии) переходит в другую (например, механическая энергия в результате трения превращается в тепловую). Однако во всех случаях энергия, отданная (в той или иной форме) одним телом другому, равна энергии, полученной последним телом. В этом смысл закона сохранения энергии.

Количественно процесс обмена энергией между взаимодействующими телами в механике характеризуется работой.

Если материальное тело движется под действием силы, то работа вычисляется как

, (3.1)

где – путь, пройденный телом.

Скалярная величина называется элементарной работой силы 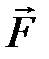на перемещении .

Механическая энергия бывает двух видов – кинетическая и потенциальная.

Кинетическая энергия тела – мера его механического движения. Она определяется работой, которую необходимо совершить, чтобы вызвать данное движение:

. (3.2)

Для тела массой , двигающегося поступательно со скоростью , кинетическая энергия равна

. (3.3)

Потенциальная энергия – часть общей механической энергии системы тел, определяемая взаимным расположением тел и характером взаимодействия между ними.

Потенциальная энергия вводится, когда взаимодействие тел осуществляется посредством силовых полей (поле упругих сил, гравитационное поле, электрическое поле и т.д.), характеризующихся тем, что работа, совершаемая действующими в них силами при перемещении центра масс тела из одной точки в другую, не зависит от того, по какой траектории это перемещение произошло, а определяется только начальным и конечным положением тела. Такие поля называются потенциальными, а силы, действующие в них, – консервативными.

Если работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, такая сила называется неконсервативной. К числу неконсервативных сил относятся, в частности, диссипативные силы, например, силы трения и сопротивления среды.

Работа консервативных сил, действующих на тело, таким образом, равна приращению потенциальной энергии тела, взятому с противоположным знаком:

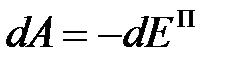, (3.4)

т.е. консервативные силы совершают работу, приводящую к убыли* потенциальной энергии тела.

Конкретный вид функции 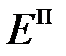зависит от характера силового поля. Например, потенциальная энергия тела массой , поднятого на высоту над поверхностью Земли, записывается как

. (3.5)

Выражение (3.5) свидетельствует о том, что потенциальная энергия равна работе силы тяжести при падении тела с высоты на поверхность Земли, где полагаем .

Так как начало отсчета потенциальной энергии выбирается произвольно, потенциальная энергия может иметь как положительное, так и отрицательное значения (кинетическая энергия всегда положительна).

Потенциальная энергия упругодеформированного тела, например, пружины определяется формулой:

, (3.6)

где 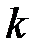– коэффициент упругости (для пружины – жесткость); – величина деформации.

Формула (3.6) получена в предположении, что потенциальная энергия недеформированного тела равна нулю.

Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними называются силы, действующие на данное тело со стороны других тел, входящих в систему; внешними – силы, действующие со стороны тел, не входящих в данную систему.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой.

Замкнутыми системы тел могут быть только приближенно, когда можно пренебречь какими-то слабыми внешними взаимодействиями по сравнению с сильными внутренними. Например, Луна вращается вокруг Земли. Если пренебречь их взаимодействием с Солнцем и другими планетами, то можно приближенно считать данную систему замкнутой.

Для замкнутых систем существуют такие функции координат и скоростей тел (материальных точек), образующих систему, которые сохраняют при движении постоянные значения. Эти функции называются интегралами движения.

Аддитивных интегралов движения три: импульс, энергия, момент импульса. Таким образом, для замкнутых систем неизменными являются три перечисленные физические величины. В соответствии с этим имеют место три закона сохранения – законы сохранения импульса, энергии и момента импульса. Рассмотрим первые два из них.

Закон сохранения импульса. При отсутствии внешних сил (рассматриваем замкнутую систему) из второго закона Ньютона в импульсной форме для системы тел (см. (2.2)) следует

, т.е. , (3.7)

где и - масса и скорость -го тела системы; - количество тел в системе.

Последнее выражение и является законом сохранения импульса: импульс замкнутой механической системы остается постоянным во времени.

Закон сохранения полной механической энергии − результат обобщения многих экспериментальных фактов. Идея закона принадлежит Ломоносову, а количественная формулировка закона дана немецкими учеными Майером и Гельмгольцем.

Итак, в замкнутой системе тел, в которой действуют только консервативные силы, полная механическая энергия системы сохраняется во времени

. (3.8)

Такие системы называются замкнутыми консервативными. Внутри системы могут происходить превращения кинетической энергии в потенциальную и обратно, но полная (суммарная) механическая энергия остается неизменной.

Для более полной и детальной информации следует обратиться к литературе, например [1-4].

1. Вывод формулы, определяющей зависимость скорости полета пули от ее массы

Сжатием пружины пистолет заряжается пулей массой . При этом в пружине будет запасена, согласно (3.6), потенциальная энергия:

, (3.9)

где – коэффициент упругости пружины; – величина деформации пружины.

Если потери энергии на преодоление трения между пулей и стволом пистолета и на сообщение кинетической энергии самой пружине незначительны, то, согласно закону сохранения полной механической энергии, вся энергия сжатой пружины при выстреле полностью превратится в кинетическую энергию пули. Так как геометрические размеры всех пуль одинаковы, а, значит, одинакова деформация пружины для любой пули и, следовательно, одинакова запасаемая пружиной потенциальная энергия, то из закона сохранения механической энергии следует, что пули различных масс , вылетая из пружинного пистолета, должны иметь одинаковые кинетические энергии:

, (3.10)

где – скорость i -й пули после выстрела.

Из (3.10) следует, что зависимость скорости пули после выстрела от ее массы:

. (3.11)

Поскольку величины и для всех пуль одинаковы, то график ожидаемой зависимости скорости пули от должен, согласно формуле (3.11), представлять собой прямую линию, проходящую через начало координат.

2. Вывод рабочей формулы для определения скорости полета пули

Пролетев небольшое расстояние между пистолетом и маятником, пуля входит в пластилин, заполняющий цилиндр, и за счет вязкого трения быстро теряет скорость. При этом часть механической энергии пули расходуется на неупругую деформацию и превращается во внутреннюю энергию пластилина и пули, то есть пластилин и пуля нагреваются. Такой удар пули и маятника, в результате которого они начинают двигаться как единое целое, называется абсолютно неупругим (см. гл.4). Механическая энергия в процессе такого удара не сохраняется (убывает).

Процесс удара является кратковременным. Если масса маятника достаточно велика по сравнению с массой пули (), то за время удара он в силу своей инерционности не успевает выйти из положения равновесия. Это позволяет считать систему «маятник-пуля» в момент удара замкнутой в горизонтальном направлении, так как при вертикальном положении маятника сила тяжести и сила натяжения подвеса направлены вертикально. В замкнутой системе выполняется закон сохранения импульса:

, (3.12)

где – проекция на горизонтальную ось скорости пули до удара (при этом скорость маятника равна нулю); 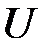– проекция скорости, приобретенная системой «маятник-пуля» сразу после удара.

Маятник вместе с пулей, получив за счет неупругого удара импульс, отклоняется от положения равновесия на угол . В процессе отклонения на маятник действуют сила тяжести, направленная вертикально вниз, и сила упругости подвеса, перпендикулярная направлению мгновенной скорости маятника. Если потеря энергии на трение в подвесе и на сопротивление воздуха не значительна, то работу при отклонении маятника совершает только сила тяжести, которая является консервативной. В замкнутой системе, между телами которой действуют только консервативные силы, выполняется закон сохранения полной механической энергии:

, (3.13)

где g – ускорение свободного падения; – наибольшая высота, на которую поднимается маятник (рис. 3.2).

В формуле (3.13) слева стоит кинетическая энергия при поступательном движении системы «маятник-пуля» сразу после удара (в этом положении потенциальная энергия принимается равной нулю), а справа – потенциальная энергия системы в момент ее остановки на высоте .

Рис.3.2

Если угол отклонения маятника от положения равновесия мал, то из рис. 3.2 следует, что

, (3.14)

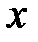где – длина нити подвеса; – горизонтальное смещение маятника (определяется механизмом ).

Из (3.14) следует

. (3.15)

Уравнения (3.12), (3.13) и (3.15) образуют систему, решая которую, можно определить скорость пули перед ударом

. (3.16)

Выражение (3.16) позволяет, осуществив прямые измерения смещения маятника и зная значения остальных величин, входящих в эту рабочую формулу, определить скорость пули путем косвенных измерений. Измерив скорости для пуль с разными массами , можно убедиться в справедливости теоретической зависимости (3.11).

3. Вывод формулы для определения погрешности

косвенных измерений скорости

Методика оценки истинных значений и погрешностей при прямых и косвенных измерениях изложена в гл. 12. Проведя прямые многократные измерения смещения маятника для одной и той же пули (см. задание к работе), можно оценить истинное значение и доверительную погрешность этой величины, записав результат в виде м.

Истинные значения остальных аргументов рабочей формулы (3.16) и их доверительные погрешности определены заранее и указаны в таблице исходных данных, расположенной около установки. Подставляя истинные значения аргументов в рабочую формулу (3.16), получим оценку истинного значения скорости пули

, (3.17)

где черта сверху означает «оценка истинного значения».

В формуле (3.16) пять аргументов (), каждый из которых определен с некоторой погрешностью. Следовательно, согласно (12.16) (см. гл. 12), формула для определения абсолютной погрешности скорости пули будет иметь вид

. (3.18)

Пользуясь формулой (3.16), вычислим частные производные от скорости по каждому из аргументов. В результате получим следующее выражение:

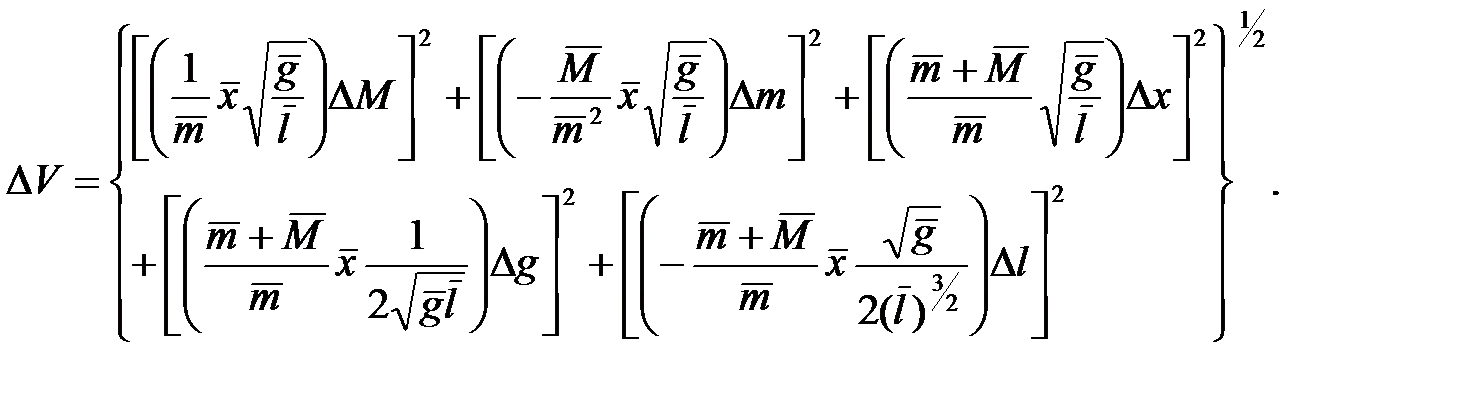(3.19)

В формулу (3.19) входит пять квадратичных членов, каждый из которых определяет вклад погрешности одного из пяти аргументов формулы (3.16) в погрешность величины . Прежде чем применять формулу (3.19), следует отдельно вычислить (приближенно) каждый из пяти квадратичных членов, чтобы сравнить их друг с другом. Сравнение покажет, точность определения каких аргументов мало влияет на абсолютную погрешность скорости. Эти члены из формулы (3.19) надо исключить, и только после этого, применив (3.19), получить оценку погрешности скорости . Численные результаты, полученные с помощью формул (3.17) и (3.19), записываются в виде

. (3.20)

Дата добавления: 2015-08-17