Цель работы – изучение метода измерения момента тормозящей силы, действующий на тело в процессе вращения; экспериментальное определение момента инерции тела.

Описание экспериментальной установки

Установка представляет собой тело со шкивом, которое вращается в шарикоподшипниках. На шкив намотана нить, один конец которой прикреплен к шкиву, а другой – к подставке массой 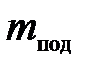. На подставку могут помещаться подгрузки массой . Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того, как груз от отметки 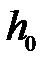опустится на полную длину нити до отметки 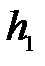(рис7.1), тело, вращаясь по инерции, поднимет груз снова на некоторую высоту до отметки h ₂.

Рис.7.1

В процессе движения часть механической энергии системы «тело-груз» расходуется на работу против тормозящей силы и, следовательно, превращается во внутреннюю энергию системы и окружающего воздуха, которые нагреваются. Из этого следует, что тело поднимет груз на высоту меньшую начальной, то есть отметка всегда будет расположена ниже отметки . Тормозящая сила складывается из силы трения в подшипниках и из силы трения о воздух при движении тела и груза.

Методика эксперимента и вывод рабочих формул

1. Вывод формулы для косвенных измерений момента тормозящей силы

Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей силы при переходе системы «тело-груз» из начального состояния в конечное равна

, (7.1)

где – механическая энергия системы «тело-груз» в начальном состоянии; – механическая энергия системы «тело-груз» в конечном состоянии.

Механическая энергия системы складывается из кинетической и потенциальной энергий. В те моменты времени, когда система покоится, кинетическая энергия равна нулю и, следовательно, механическая энергия становится равной только потенциальной энергии системы. Такие состояния системы возникают в начальный момент времени, когда груз находится на отметке 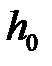, и в тот момент, когда, спустившись вниз, груз за счет вращения тела поднимается до отметки (рис.7.1). Если принять, что на высоте 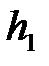потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно

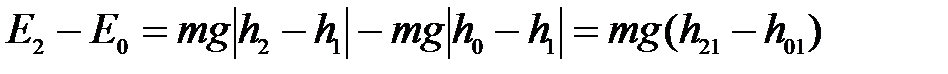, (7.2)

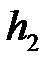где m – масса подставки с подгрузками; – расстояние между отметками и ; – расстояние между отметками и .

Будем считать, что момент тормозящей силы в основном связан с вращательным движением тела, т. е. тормозящей силой, действующей на груз, пренебрежем. Тогда элементарная работа момента тормозящей силы равна скалярному произведению

,

где – вектор момента тормозящей силы; – вектор бесконечно малого углового перемещения тела.

Оба вектора и направлены вдоль оси вращения, но в противоположные стороны. Следовательно,

.

Полная работа тормозящей силы, если предположить, что ее момент постоянен, равна

, (7.3)

где – угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки 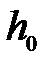до отметки ).

При движении груза вниз от отметки 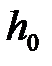до отметки 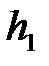со шкива сматывается нить длиной 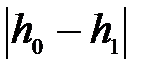. Учитывая, что длина окружности шкива равна и каждый оборот шкива соответствует углу радиан, найдем угол поворота шкива при движении груза вниз:

радиан. (7.4)

Очевидно, что при дальнейшем вращении тела до момента, когда груз остановится на отметке , оно повернется на угол

радиан.

Тогда общий угол поворота тела, соответствующий движению груза от отметки 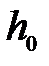до отметки , равен

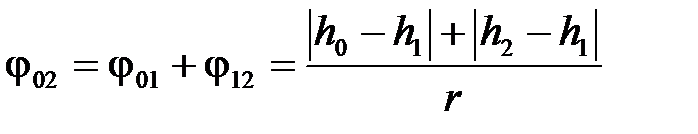радиан. (7.5)

Подставляя (7.2) и (7.3) в (7.1), найдем

.

Отсюда, используя (7.5), получаем формулу для определения величины момента тормозящей силы

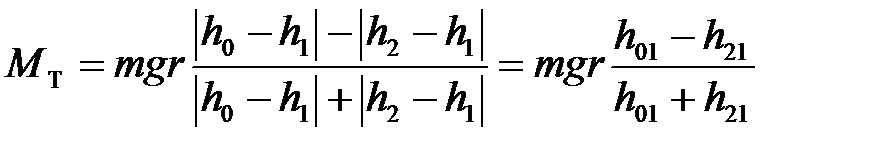. (7.6)

2. Вывод формулы для косвенных измерений момента инерции тела (с учетом момента тормозящей силы)

Рассмотрим систему «тело-груз» в начальный момент времени, когда груз находится на отметке 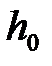, а в качестве конечного выберем тот момент времени, когда груз опустился до нижней отметки , соответствующей полной длине нити. Опять будем исходить из энергетического соотношения (7.1).

Для выбранных начального и конечного состояний получим

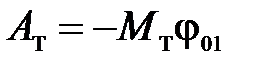, (7.7)

где 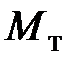– момент тормозящей силы (7.6); – угол поворота тела, соответствующий перемещению груза от отметки до и определяемый по формуле (7.4).

Начальная механическая энергия системы «тело-груз» равна

. (7.8)

Конечная механическая энергия системы складывается из кинетической энергии вращательного движения тела и кинетической энергии поступательного движения груза в момент прохождения им отметки :

, (7.9)

где – момент инерции тела; – угловая скорость вращения тела в момент 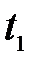(рис.7.1); – скорость поступательного движения груза в момент .

Таким образом, в процессе движения груз за счет упругого растяжения нити опускается чуть ниже отметки , тормозится нитью, а затем за счет упругого сжатия нити возвращается на эту отметку.

Предполагая, что движение системы является равноускоренным, для скорости груза на отметке 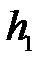получаем

, (7.10)

где – время, за которое груз опустится от отметки до .

Угловая скорость вращения тела в тот же момент времени равна

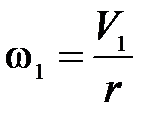, (7.11)

где – радиус шкива, на который намотана нить.

Подставляя (7.7), (7.8), (7.9) в (7.1), получим

.

Из этой формулы, учитывая (7.4), (7.10) и (7.11), выражаем момент инерции :

, (7.12)

где – момент тормозящей силы, который вычисляется по формуле (7.6).

3. Вывод формул для расчета погрешностей косвенных измерений момента тормозящей силы и момента инерции тела

Методика определения оценок истинных значений величин и погрешностей при прямых и косвенных измерениях описана в главе «Обработка результатов измерений физических величин». При выполнении данной лабораторной работы прямыми будут являться измерения длины и времени . Остальные величины, входящие в рабочие формулы (7.6) и (7.12), измеряются заранее и их истинные значения с указанием погрешностей приведены в таблице исходных данных, помещенной около экспериментальной установки.

Выполнив прямые многократные измерения величин 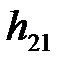и (см. задание к работе) и проведя их статистическую обработку по методике, описанной в гл.12, найдите 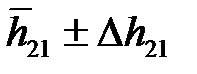и для выбранного значения доверительной вероятности. Эти величины будут в дальнейшем использованы для оценки истинного значения и погрешности при косвенных измерениях.

Подставляя в рабочую формулу (7.6) истинные значения всех аргументов, получим оценку истинного значения момента тормозящей силы:

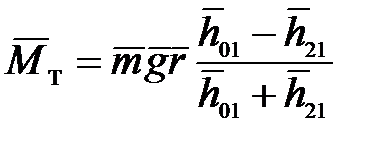, (7.13)

где черта над величиной означает «оценка истинного значения».

Абсолютная погрешность косвенных измерений величины определяется формулой

.

Взяв частные производные по всем аргументам, получаем

. (7.14)

В формулу (7.14) входят пять квадратичных членов. Вклад каждого из них в погрешность величины 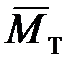не одинаков. Поэтому, чтобы упростить вычисления, прежде чем применять эту формулу, необходимо оценить вклад каждого квадратичного слагаемого и оставить в формуле только наибольшие. Эта оценка, кроме того, позволит выявить те величины, точность измерения которых определяет точность получаемого результата.

Оценку истинного значения величины момента инерции тела, определяемого в опытах с помощью формулы (7.12), получим, подставив в нее истинные значения входящих аргументов:

. (7.15)

Абсолютная погрешность косвенных измерений величины определяется формулой

.

Взяв частные производные по всем аргументам, получаем

. (7.16)

В формулу (7.16) входит шесть квадратичных членов. Один из них (пятый) связан с погрешностью величины , которая определяется формулой (7.14). Как было отмечено ранее, прежде, чем применять формулу (7.16), необходимо оценить вклад каждого квадратичного слагаемого, сохранив только наибольшие.

Дата добавления: 2015-08-17