Лабораторная работа 9

Цель работы –определение момента инерции физического маятника с применением уравнения колебаний.

Описание экспериментальной установки

Установка представляет собой физический маятник – твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр масс.

Физический маятник в данной работе состоит из барабана массой m ₁ с осью вращения О, стержня массой m ₂ и двух грузов с одинаковыми массами m ₃, которые можно закреплять в нужном положении на стержне (рис.9.1).

Рис.9.1

Методика эксперимента и вывод рабочих формул

Пока сила тяжести , приложенная к центру масс С, направлена вдоль оси стержня (рис.9.1, а), система находится в равновесии. Если отклонить стержень на некоторый малый угол (рис.9.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна

, (9.1)

где ; L – расстояние между осью вращения О и центром масс С.

Вращающий момент М, создаваемый силой , при малых углах равен

.

Он вызывает ускорение при вращательном движении маятника. Связь между этим ускорением и моментом силы тяжести задается основным уравнением динамики вращательного движения:

, (9.2)

где J – момент инерции маятника относительно оси О.

Введем обозначение

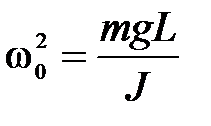. (9.3)

Тогда из уравнения (9.2) получаем

. (9.4)

Уравнение (9.4) описывает колебательный процесс с циклической частотой .

Период колебаний равен

. (9.5)

Из формулы (9.5) выразим момент инерции

. (9.6)

Если положение центра масс системы не изменяется, то величина L постоянна и в формулу (9.6) можно ввести постоянный коэффициент

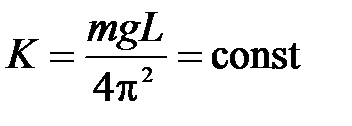. (9.7)

Измеряя время t, в течение которого происходит n полных колебаний, найдем период как

.

Подставив T и K в (9.6), получим рабочую формулу

. (9.8)

С помощью формулы (9.8) производятся косвенные измерения момента инерции физического маятника относительно оси О.

С другой стороны, момент инерции J зависит от положения грузов 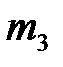на стержне. Переместим грузы 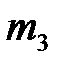вдоль стержня так, чтобы они располагались симметрично относительно некоторой точки А. Эта математическая точка выбрана произвольно вблизи середины стержня. Центр масс системы при этом сохраняет свое местоположение. Будем считать размеры грузов малыми по сравнению с расстояниями и (рис.9.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением

, (9.9)

где – момент инерции системы без грузов; x – расстояние груза до точки А; l – расстояние от точки А до оси вращения маятника О.

Выполнив преобразования в (9.9), получаем

, (9.10)

где – момент инерции маятника при расположении грузов в точке А.

В процессе выполнения лабораторной работы проверим зависимость (9.10), получив величины и 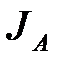экспериментально с помощью формулы (9.8).

Для более полной и детальной информации следует обратиться к литературе, например [1-4].

Задание к работе

1. Получите допуск к выполнению лабораторной работы у преподавателя.

2. При подготовке к лабораторной работе получите расчетную формулу для погрешности косвенных измерений D J момента инерции (см. гл. 12). Учтите, что момент инерции определяется с помощью рабочей формулы (9.8).

3. Подготовьте таблицу для статистической обработки прямых пятикратных измерений времени t (в качестве образца возьмите табл. 12.3 гл. 12).

4. Подготовьте таблицу для исследования зависимости .

5. Включите электронный секундомер. Нажатием кнопки «Режим» установите режим 3 (светится индикатор «Реж. 3»), при этом отключится тормозное устройство, удерживающее тело.

6. Приступая к работе, поместите оба груза в точку А.

7. Отклоните маятник рукой на небольшой угол , и в момент отпускания маятника включите секундомер нажатием кнопки «Пуск». Отсчитав 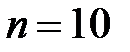полных колебаний маятника, остановите секундомер нажатием кнопки «Стоп». Запишите полученное время в таблицу измерений.

8. Проведите пятикратные измерения времени t десяти полных колебаний физического маятника, не меняя положение грузов.

9. Рассчитайте среднее время и определите доверительную погрешность измерения .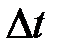

10. Используя рабочую формулу (9.8), определите значение момента инерции , а по формуле, полученной в пункте 2 задания к работе, определите погрешность измерения этой величины . Результат запишите в виде . Результат занесите в таблицу для значения .

11. Раздвиньте грузы симметрично относительно точки А на расстояние (рис.9.1). Рекомендуется расстояние взять равным тому значению. Проведите однократные измерения времени t десяти полных колебаний физического маятника.

12. Повторите опыт, описанный в пункте 11, для пяти различных расстояний .

13. Определите момент инерции маятника при различных расстояниях 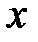с помощью формулы (9.8). Результаты занесите в таблицу.

14. Пользуясь таблицей, постройте график зависимости . Нанесите на этот же график теоретическую зависимость, определяемую формулой (9.10). Проведите сравнение и анализ полученных результатов.

Контрольные вопросы

1. Какова цель данной лабораторной работы?

2. Момент инерции тела, его физический смысл.

3. Сформулируйте и примените к данной работе основной закон динамики вращательного движения твердого тела.

4. Что такое центр масс системы?

5. Почему местоположение центра масс маятника не меняется при изменении расстояния x от грузов до точки A?

6. Найдите момент инерции системы относительно центра масс, задав или измерив нужные для этого величины.

7. Сформулируйте закон сохранения энергии и запишите его применительно к колебаниям физического маятника.

8. Получите рабочую формулу (9.8) и зависимость (9.10).

9. Получите формулу для расчета погрешности косвенных измерений момента инерции.

10. Сформулируйте теорему Штейнера и примените ее к исследуемой системе.

11. Почему в работе предлагается построить график зависимости момента инерции от квадрата величины , а не от самой этой величины?

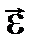12. Что такое момент силы , угловая скорость , угловое ускорение , угловое перемещение 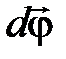, как направлены эти векторы?

10. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ

МЕТОДОМ КЛЕМАНА И ДЕЗОРМА

Дата добавления: 2015-08-17