Статическая обработка результатов косвенных измерений

При косвенных измерениях результаты получаются при помощи вычисления по формулам, в которые входят результаты прямых измерений, табличные величины, справочные данные и т.д., определённые с конечной точностью.

Предположим, что мы определяем значение функции от непосредственно измеряемых величин (или найденных справочных или заданных) 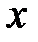, , 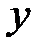. Обозначим через

(12.12)

значение функции для каждого опыта .

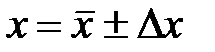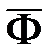Пользуясь конечным видом функции и имеющимися значениями , , , необходимо оценить и величину погрешности , характеризующую разброс значений , относительно . Для определения этих оценок удобно использовать два практически тождественных по результатам метода.

Метод выборок – применяется в тех случаях, когда значения 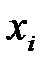, , определяются из различных опытов и для данного 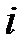могут существенно отличаться от таких же величин для другого значения 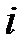. Статическое усреднение отдельных величин 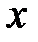, , в этом случае не имеет смысла. Тогда поступают следующим образом:

1) по формуле (12.12) определяют значения для каждого опыта ;

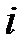2) по формуле (12.3) вычисляют среднее значение ;

3) вычисляют абсолютную погрешность так же, как в случае прямых измерений;

4) вычисляют относительную погрешность по формуле, аналогичной (12.10):

; (12.13)

5) записывают окончательный результат в виде

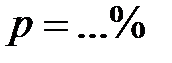, , . (12.14)

Метод, основанный на применении формулы полного дифференциала, используется в тех случаях, когда величины , , определяются из одного эксперимента и могут быть статически обработаны до подстановки в формулу (12.12). Тогда среднее значение вычисляют по формуле

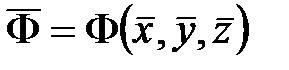, (12.15)

а погрешности находят двумя способами.

Первый способ. На основании формулы полного дифференциала

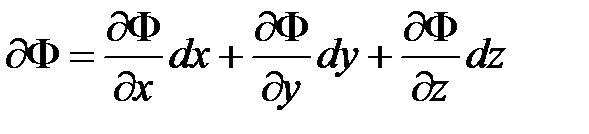
и процедуры квадратичного усреднения для погрешности (с учётом того, что она достаточно мала) можно получить следующее выражение

, (12.16)

где индексы , , у частных производных указывают на то, что численные значения этих производных берутся при , , 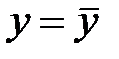, а , , 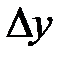– соответствующие погрешности прямых измерений или табличных, справочных величин. Формула (12.16) может применяться и тогда, когда значения 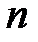при измерениях 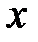, , (например, за счёт промахов) различны.

Зная абсолютную погрешность , легко найти относительную погрешность по формуле (12.13) и записать результат в виде (12.14).

Второй способ. Разделив обе части (12.16) на 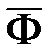и учитывая, что

,

,

,

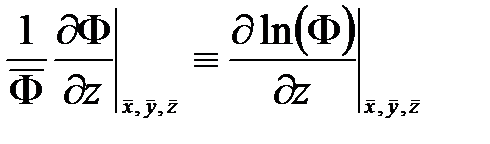получим формулу для относительной погрешности

. (12.17)

Если функция имеет логарифмический вид (независимые переменные входят как сомножители), то формула (12.17) приводит к более простым выкладкам, чем формула (12.16).

Определив , можно найти и абсолютную погрешность по формуле

. (12.18)

Зная абсолютную погрешность , можно записать результат в виде (12.14).

Дата добавления: 2015-08-17