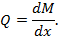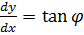Пример 7.

Р=7

q=3

Пронумеруем границы характерных участков. Расчет начнем с участка 1-2. Для этого вновь прибегнем к уже ставшему стандартным приему – мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис.37,а). При этом эпюра на участке 1-2 является аналогом первого частного случая (см. рис.18), ее характер и величина изгибающего момента правее точки 2 известны (рис.37,б).

Рис.37

3

q=3

а)

б)

Р=7

Р=7

P×L=7×3=21

Р=7

3

M=21

3×4²/2=24

21 +7×4= 49  

=

а)

б)

в)

3

3

М=21

q=3

Р=7

Р=7

q=3

q=3

q=3

На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставим ее в сечение 3 (рис38,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2-3. Приложим к нему сосредоточенный момент М=21, отложенный ниже нейтральной оси в сечении правее т.2 (см. рис.38,б) и растягивающий, таким образом, нижние волокна. Также в сечение 2 переносим сосредоточенную силу Р=7. Кроме того, на участке 2-3 (рис.38,б) добавляем равномерно-распределенную нагрузку интенсивностью q = 3.

- 25 -

Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие сосредоточенного момента М=21 соответствует частному случаю 2 (рис.21), приводя к растяжению нижних волокон. Отложим ординату 21 ниже нейтральной оси (рис.38,в); независимое действие сосредоточенной Р=7 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна P×L= 7×4= 28. Отложим эту ординату ниже нейтральной оси. Воздействие равномерно-распределенной нагрузки на участок 2-3 приводит к возникновению изгибающего момента, растягивающего верхние волокна (по третьему частному случаю) и равного М=q×L²/2=3×4²/2=24. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=21+28-24=25. Этот момент растягивает нижние волокна. В пределах характерного участка 2-3 эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью вниз. Результат проведенного расчета на участке 2-3 (пока без построенной эпюры) – на рис.36,г.

Рис.38

г)

На этом рисунке пунктиром показаны два варианта прохождения криволинейной эпюры М через точки с ординатами 25 и 21 – либо по пологой кривой, либо по кривой, имеющей точку экстремума. Для конкретизации характера поведения данной эпюры обратим свои взоры к еще одному важному разделу расчета стержневых систем, а именно, к процессу построения эпюры поперечных сил.

Как построить эпюру поперечных сил по имеющейся эпюре изгибающих моментов?

В основе данной процедуры лежит известное нам соотношение, вытекающее из теоремы Журавского, а именно:

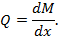
Смысл этого соотношения в том, что поперечная сила Q является первой производной по моменту M. Напомним, что геометрический смысл первой производной – это тангенс угла наклона φ касательной t, проведенной в расчетной точке (рис.39).

-

φ

t

26 –

Рис.39

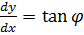
В рамках предлагаемой процедуры следует различать два случая:

- эпюра изгибающих моментов – прямолинейна;

- эпюра изгибающих моментов криволинейна (рассмотрим случай очертания эпюры по квадратной параболе).

Дата добавления: 2015-08-17