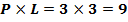Пример 1. Анализ предложенной задачи приводит к следующим выводам:

Анализ предложенной задачи приводит к следующим выводам:

- данная конструкция является консольной балкой;

- определение опорных реакций в такой конструкции необязательно;

- построение эпюры моментов следует начинать со свободного конца;

- число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков для лучшего усвоения предлагаемого алгоритма построения эпюры изгибающих моментов. Расчет начинаем с участка 1-2. Для этого прибегнем к такому приему – мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис.25,а). При этом участок 1-2 становится аналогом первого частного случая (см. рис.18), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис.25,б).

3

P₂=3

P₁=7

а)

Рис.25

P₂=3

б)

- 14 –

На следующем шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис26,а). При этом балка в сечении 2 восстанавливает свои кинематические характеристики. Далее рассмотрим участок 2-3. Приложим к нему сосредоточенный момент М=9, отложенный выше нейтральной оси в сечении, правее т.2 (см. рис.25,б) и растягивающий, таким образом, верхние волокна. Кроме того, на участок 2-3 переносим сосредоточенную силу Р₂=3, прикладываем ее в точке 2 (рис.26,б) и добавляем сосредоточенную силу Р₁= 7. Определим равнодействующую двух вертикальных сил в сечении 2: R = P₁-P₂= 7-3= 4 (рис.26,в). Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=9 соответствует частному случаю 2 (рис.21), приводя к растяжению верхних волокон. Отложим ординату 9 выше нейтральной оси (рис.26,г); независимое действие сосредоточенной силы R=4 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна М₃=Р×L=4×4=16. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16-9=7. Этот момент растягивает нижние волокна. В пределах характерного участка 2-3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2-3 – на рис.26,д. На рис. 26,е изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой сосредоточенных сил.

3

P₂=3

P₁=7

3

P₂=3

P₁=7

3

M=9

M=9

3

R=4

M=9

4×4=16

=

R=4

M=9

7

9

P₂=3

P₁=7

9

7

Рис.26

а)

б)

в)

г)

д)

е)

R=4

- 15 –

Обратим внимание на характерную особенность полученной эпюры в сечении 2. При действии сосредоточенной силы на эпюре изгибающих моментов в этом сечении наблюдается перелом (или же излом) в сторону действия этой нагрузки. Это свойство широко применяетсяпри визуальном контроле правильности построения эпюры изгибающих моментов.

P=7

M=17

Пример 2.

Анализ новой задачи вновь приводит к таким выводам:

- данная конструкция является консольной балкой;

- определение опорных реакций в такой конструкции необязательно;

- построение эпюры моментов следует начинать со свободного конца;

- число характерных участков равно двум (см. стр.10).

Вновь пронумеруем границы характерных участков. Расчет начинаем с участка 1-2. Для этого вновь прибегнем к уже известному приему – мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис.27,а). При этом участок 1-2 становится аналогом второго частного случая (см. рис.21), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис.27,б).

а)

Рис.27

б)

3

M=17

P₁=7

На следующем шаге вновь ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис28,а). При этом балка в сечении 2 восстанавливает свои кинематические характеристики. Далее рассматриваем участок 2-3. Приложим к нему сосредоточенный момент М=17, отложенный выше нейтральной оси в сечении правее т.2 (см. рис.27,б) и растягивающий, таким образом, верхние волокна. Кроме того, на участке 2-3, прикладываем в точке 2 (рис.28,б) сосредоточенную силу Р₁=7. Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=17 соответствует частному случаю 2 (рис.21), приводя к растяжению верхних волокон. Отложим ординату 17 выше нейтральной оси (рис.28,в); независимое действие сосредоточенной силы Р₁=7 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3

- 16 -

равна М₃=Р×L=7×4=28. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=28-17=11. Этот момент растягивает нижние волокна. В пределах характерного участка 2-3 эпюра изгибающих моментов прямолинейна. Результат рассмотрения участка 2-3 – на рис.26,г. На рис. 26,д изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой нагрузок.

M=17

M=17

177

P₁=7

17

111

Рис.28

а)

б)

г)

д)

3

M=17

P₁=7

3

P₁=7

3

M=9

7×4=28

=

в)

P₁=7

P₁=7

M=17

При визуальном контроле построенной эпюры с удовлетворением отмечаем наличие перелома под действием сосредоточенной силы Р₁, что указывает на правильность наших действий.

Дата добавления: 2015-08-17