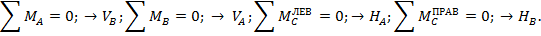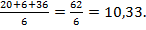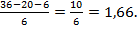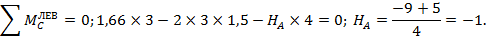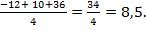Построение эпюр внутренних усилий в трехшарнирных рамах.

Что понимается под определением «трехшарнирная рама»?

Трехшарнирная рама – один из видов т.н. трехшарнирных стержневых систем, среди которых – уже упомянутые трехшарнирные рамы, трехшарнирные арки и фермы. Далее расчету будут подвергнуты два типа подобных рам: трехшарнирная рама «классического» очертания с опорами на одном уровне или сводящиеся к этому типу, а также трехшарнирная рама «с затяжкой».

С

А

H_B

H_A

V_A

V_B

L

H

q(x)

В

x

Какова последовательность расчета классической рамы, изображенной на рис.53?

Рис.53

Начнем со структурного анализа новой конструкции. Она представляет собой три жестких диска- АС, СВ и «землю»- объединенные между собой тремя шарнирами А, В и С, не лежащими на одной прямой. Подобная конструкция геометрически неизменяема.

- 36 -

Пусть трехшарнирная рама находится под действием произвольной системы сил q(x). Расстояние между опорами А и В принято называть пролетом рамы L, H – это высота рамы или же ее «подъем», V_A и V_B - ee вертикальные реакции, а H_A и H_B – реакции горизонтальные или «распор». Соединительный шарнир С называют «ключевым» или «ключом».

Приступим к определению опорных реакций. В первую очередь запишем выражение для ΣM_А=0 – «сумма моментов всех внешних и внутренних сил относительно шарнира А равна 0». Так как линии действия горизонтальных и левой вертикальной реакций проходят через точку А их моменты относительно нее равны 0. Поэтому из этого уравнения однозначно определяется правая вертикальная опорная реакция. Из аналогичного уравнения относительно точки В получим величину и направление левой вертикальной реакции. Для определения левой горизонтальной реакции применим такой расчетный прием: запишем выражение для суммы моментов всех внешних и внутренних сил (включая известную уже левую вертикальную реакцию), приложенных к левой, относительно ключевого шарнира С, части рамы, и приравняем ее 0. Аналогично поступим при определении правой горизонтальной реакции. Схема определения опорных реакций в классической трехшарнирной раме приведена ниже.

После определения опорных реакций строятся эпюры внутренних усилий.

P=5  

H_A

q=2

m=6

С

А

H_B

V_A

V_B 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

В

Пример 9.

ΣM_A=0; 5×4+6+2×6×3-V_B×6=0; V_B=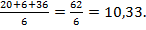  

- 37 –

Знак «+» указывает на правильность первоначального выбора направления опорной реакции V_B. Определим опорную реакцию V_A.

ΣM_B=0; 5×4 + 6 - 2×6×3 + V_A×6 = 0; V_A=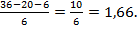

При записи «моментных» уравнений, типа приведенных только что выше, следует руководствоваться таким соображением: моменты, вращающие в разные стороны, должны иметь разные знаки. Что и было использовано при определении вертикальных реакций для данной трехшарнирной рамы.

а)

q=2

P=5  

H_A=1

С

А

V_A=1,66

б)

q=2

m=6

H_B=4

V_B=10,33 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

В

С

Переходим к определению левой горизонтальной реакции. Для этого «рассечем» раму по соединительному шарниру С и рассмотрим равновесие ее левой части (рис.54,а). При определении правой горизонтальной реакции рассмотрим равновесие правой относительно ключевого шарнира С части рамы (рис.54,б).

Рис.54

Знак «минус» указывает на необходимость изменения направления полученной реакции, что и сделано на рис.54,а.

P=5  

q=2

m=6

С

10,33 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

Рис.54

1,66

А

В

Далее, пронумеруем границы характерных участков, а по направлению опорных стержней рамы приложим найденные опорные реакции.

- 38 –

Следует запомнить, что отправными точками для построения эпюры М могут служить лишь те сечения, для которых одновременно известны величины и моментов и поперечных сил. Таким образом, «стартовать» по нашему желанию мы можем с точек А, В и 3. Наметим последовательность построения эпюры изгибающих моментов для данной рамы. Сначала рассмотрим участок 3-2, затем участок В-2, «вырежем» узел 2 и получим момент левее узла 2. После чего изменим «движение» по раме и последовательно рассмотрим участки А-1 и 1-С.

m=6

10,33 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

В

а)

б)

С

в)

P×L=4×4=16

V_А=1,66 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

6+16=22

q=2

1,66

А

P×L=1×4=4

г)

Рис.55 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

5 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

д)

M₁^ПРАВ=4

е)

q×L²/2=2×3²/2=9

4+1,66×3=4+5=9

Участок 3-2 – это аналог второго частного случая (стр.21), растянутые волокна – верхние (рис.55,а). Участок В-2 – аналог первого частного случая (стр.18) – растянутые волокна справа от нейтральной оси (рис.55,б), а правая вертикальная реакция не влияет на изменение момента на этом участке. На рис.55,в показан вырезанный узел 2, результирующий момент М₂^ЛЕВ=16+6=22. Для равновесия узла он должен быть направлен против часовой стрелки, т.е. растягивать верхние волокна. Участок А-1 – аналог первого частного случая (стр.18), растянутые волокна – справа от нейтральной оси (рис.55,г), а левая вертикальная реакция в расчете не участвует.

= 0

Для перехода на горизонтальный участок 1-С, т.е. для вычисления момента правее узла 1, вырежем и уравновесим этот узел. Искомый момент М₁^ПРАВ=4 и растягивает нижние волокна, что видно из рис.55,д. Перейдем на участок 1-С, установив мысленно жесткую заделку левее шарнира С. При расчете этого участка необходимо учесть влияние левой вертикальной реакции и разместить ее в точке 1. Используя принцип независимости действия сил, вычислим изгибающий момент левее точки С. Он, как и ожидалось, равен 0 (рис.55,е). Для выяснения характера криволинейной эпюры моментов на участке 1-2, предварительно построим здесь эпюру поперечных сил Q (рис.56).

q=2

С

?

(22+4)/6=4,33

-

+

2×6/2=6

2×6/2=6

+

=

- -

+

!

-

6-4,33=1,67

Рис.56

- 39 -

6+4,33=10,33

P=5  

q=2

m=6

А

В

С

М

1,66

10,33 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

Q

+

+

+

-

Узел 1

Узел 2

Рис.57

Из анализа рис.56 становится очевидным наличие экстремума на участке с криволинейным очертанием эпюры М (1-2) в сечении, где происходит изменение знака поперечной силы. На рис.57 показаны полные эпюры изгибающих моментов М и поперечных сил Q в рассчитываемой раме, а на рис.58 – алгоритм построения эпюры продольных сил N.

Рис.58

1,66

10,33

N

-

-

-

Узел 1

10,33

ΣX=0; N_2-3+4-4=0; N_2-3=0. ΣY=0; N_2-B+10,33=0; N_2-B= -10,33.  

ΣX=0; N_1-С+5-1=0; N_1-C= -4; ΣY=0; N_1-A+1,66=0; N_1-A= -1,66.

N_2-B

N_2-3

Узел 2

N_1-С

N_1-А

1,66

Вырежем последовательно с эпюры Q узлы 1 и 2.

- 40 –

Каковы особенности расчета трехшарнирной рамы с затяжкой?

муфта

Рассмотрим это на конкретной задаче.

P=6  

H_A=12

q=2

m=10

С

А

V_A=14,5

V_B=8,5 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

В

Рис.59 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

X

X

Пример 10.

Особенностью такой конструкции является наличие только одной из горизонтальных опор (в отличие от классической трехшарнирной рамы) и появление нового конструктивного элемента – «затяжки» 3-4. Обозначим все характерные сечения рамы, а также покажем положительные направления опорных реакций (что полностью является нашим произволом). Вертикальные реакции определяем аналогично классической раме, т.е.:

ΣM_A=0; -6×2+10+2×6×3-V_B×4=0; V_B=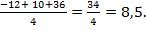  

ΣM_B=0; 6×2 + 10 + 2×6×3 + V_A×4 = 0; V_A=

На заданной схеме (рис.59) зафиксируем полученный результат. Знак «плюс» у найденной реакции подтверждает правильность наших предположений относительно ее направления. Теперь определим левую вертикальную реакцию:

ΣX=0; 2×6 + H_A = 0; H_A=

Знак «минус» указывает на необходимость поменять первоначальное направление искомой реакции на противоположное (что фиксируем на заданной схеме). Горизонтальную реакцию H_A получим следующим образом:

Меняем направление горизонтальной реакции на противоположное (см.рис.59). Для определения усилия в затяжке (работающей при отсутствии на ней поперечной нагрузки только на «растяжение-сжатие»), т.е. продольной силы, разделим раму на две части, проведя сечение 1-1 через ключевой шарнир С. Этим самым мы переводим усилие X в затяжке из разряда внутреннего в разряд внешнего. Для сохранения структурной неизменяемости вводим специальное устройство, называемое «муфтой». Зададим положительное направление усилия

- 41 -

X «от узла». Затем запишем уравнение, аналогичное примененному в случае с классической рамой, для определения одной из горизонтальных реакций:

P=6  

q=2

m=10

С

А

14,5

8,5 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

В

X=2,33

X=2,33

Рис.60 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

Знак «минус» указывает на то, что усилие в затяжке сжимающее, т.е. отрицательное. Выбор правого моментного уравнения обусловлен простотой определения усилия X. Приступим к построению эпюры М и по направлению опорных стержней рамы приложим найденные опорные реакции, а в точках 3 и 4 – найденные усилия в затяжке (рис.60).

. Наметим последовательность построения эпюры изгибающих моментов для данной рамы. Сначала рассмотрим участок 4-2, затем участок 5-2, «вырежем» узел 2 и получим момент левее узла 2. После чего изменим «движение» по раме и последовательно рассмотрим участки 3-1 и А-1, затем вырежем узел 1 и получим момент правее узла 1. Заметим, что на участке В-2 эпюра моментов отсутствует.

m=10

а)

в)

М ₂^ЛЕВ = 7+10=17

q=2

= 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

2,33

г)

1

q×L²/2=2×3²/2=9

2,33×3=7

3

Рис.60 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

2,33

б)

P×L=2,33×3=76

Участок 5-2 – это аналог второго частного случая (стр.21), растянутые волокна – верхние (рис.61,а). Участок 4-2 – аналог первого частного случая (стр.18) – растянутые волокна слева от нейтральной оси (рис.61,б). На рис.61,в показан вырезанный узел 2, результирующий момент М₂^ЛЕВ=7+10=17. Для равновесия узла он должен быть направлен против часовой стрелки, т.е. растягивать верхние волокна.

- 42 –

Используя принцип независимости действия сил, рассмотрим участок 3-1 и вычислим изгибающий момент выше точки 1. Независимое действие сосредоточенной силы 2,33 соответствует частному случаю 1 (стр.18), приводя к растяжению правых волокон. Отложим ординату 7 правее нейтральной оси (рис.60,г). Воздействие равномерно-распределенной нагрузки на участок 3-1 приводит к возникновению изгибающего момента, растягивающего левые волокна (по третьему частному случаю) и равного М=q×L²/2=2×3²/2=9. Суммарное воздействие этих двух факторов приводит к растяжению левых волокон, а вызванный ими изгибающий момент равен 2.. В пределах характерного участка 3-1 эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью вправо. Для выяснения характера криволинейной эпюры моментов на участке 3-1, предварительно построим здесь эпюру поперечных сил Q (рис.61,а).

а)

2/3=0,66

(9+5)/2=7

Рис.61

+

б)

q=2

= 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

А

1

q×L²/2=2×3²/2==9

12×3=36

в)

М₁^ПРАВ =29

г)

27/3=9

+

+

+

(2×3)/2=3

(2×3)/2=3

=

-

9+3=12

+

9-3=6

М

+

+

(2×3)/2=3

(2×3)/2=3

-

0,66+3=3,66

-

=

+

!

3-0,66=2,34

Используя принцип независимости действия сил, рассмотрим участок 1-A и вычислим изгибающий момент ниже узла 1. Независимое действие сосредоточенной силы 12 соответствует частному случаю 1 (стр.18), приводя к растяжению правых волокон. Отложим ординату 36 правее нейтральной оси (рис.61,в). Воздействие равномерно-распределенной нагрузки на участок 1-А приводит к возникновению изгибающего момента, растягивающего левые волокна (по третьему частному случаю) и равного М=q×L²/2=2×3²/2=9. Суммарное воздействие этих двух факторов приводит к растяжению правых волокон, а вызванный ими изгибающий момент равен 27. В пределах характерного участка 1-А эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью вправо. Для

- 43 -

выяснения характера криволинейной эпюры моментов на участке 1-А, предварительно построим здесь эпюру поперечных сил Q (рис.61,г). Вид построенной эпюры поперечных сил на этом участке указывает на отсутствие точки перегиба. На рис.61,д показана эпюра изгибающих моментов для данной рамы. Обратим внимание на «перелом» эпюры моментов под действием сосредоточенной силы в шарнире С. На рис.62,а показана эпюра поперечных сил, построенная по эпюре М. Отметим скачок поперечной силы в ключевом шарнире на величину сосредоточенной силы Р=6. На рис.62,б и в – последовательность построения эпюры продольных сил N. Сама эпюра продольных сил – на рис.62,г. В связи с отсутствием продольной нагрузки на участках 3-1 и 4-2 соответствующие продольные силы автоматически равны 0. Продольная сила в затяжке равна по величине и знаку усилию X.

!

Рис.62 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

Узел 1

Узел 2

8,5

2,33

ΣX=0; 2,34-2,34=0; ΣY=0; N_2-B+8,5=0; N_2-B= -8,5.  

ΣX=0; N_1-С+3,66-6=0; N_1-C= 2,34; ΣY=0; N_1-A-14,5=0; N_1-A= 14,5.  

N_2-B

2,34

N_1-С

N_1-А

14,5

3,66

7/3=2,33

Узел 2

3,66

2,34

29/2=14,5

-

Q

=

!

+

+

-

-

17/2=8,5

+

Узел 1

а) 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

б) 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

в) 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

г) 9.еской трехшарнирной раме строятся эпюры внутренних услий. Схема определения опорных реакций реакцию

2,34

N

=

+

+

14,5

-

8,5

2,34

Дата добавления: 2015-08-17