
|
Читайте также: |
Если в системе автоматического регулирования имеется лишь одна одно- значная нелинейность
y = F (x), (9.7)
то, объединив вместе все остальные (линейные) уравнения системы, мож- но всегда

|
y = F (x 1)
(б)
получить общее уравнение линейной части системы (рисунок 9.2,а) в виде
Q (p) x = R (p) y, (9.8)
где
Q (p) x = a 0
p n 1 +... + a
p + an,
R (p) x = b 0
p m + b p m 1+... + b
m 1
p + am,
причем будем считать т < п.
Пусть нелинейность y=F(x) имеет любое очертание, не выходящее за пределы заданного угла arctg k (рисунок 9.2, б), т. е. при любом х,
0< F(x) < kx. (9.9)
ние
Пусть многочлен Q(p) или, что то же, характеристическое уравне-
линейной части Q(p) =0 имеет все корни с отрицательными вещественными частями или же кроме них имеется еще не более двух нулевых корней. Дру-
гими словами, допускается, чтобы
an = 0 или
an = 0 и
an 1= 0 в выражении
Q(p), т. е. не более двух нулевых полюсов в передаточной функции линей- ной части системы
 W (p) = R (p).
W (p) = R (p).
Q (p)
Приведем без доказательства формулировку теоремы В.М.Попова: для установления устойчивости нелинейной системы достаточно подобрать та-
кое конечное действительное число h, при котором при всех
CO z 0
 Re(1 + jCOh) W (jCO) + 1 > 0, (9.10)
Re(1 + jCOh) W (jCO) + 1 > 0, (9.10)
k
где
W (jCO)
- амплитудно-фазовая частотная характеристика линейной части
системы. При наличии одного нулевого полюса требуется еще, чтобы
Im W (jCO) í 00
при
CO í 0,
а при двух нулевых полюсах
Re W (jCO) í 00
при CO í 0, a
Im W (jCO) -< 0
при малых CO.
Теорема справедлива также и при наличии в знаменателе Q(p) переда- точной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия, на- зываемые условиями предельной устойчивости.

Рисунок 9.3 График W * (jCO)
Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характери- стики W * (jCO), которая определяется следующим образом:
Re W * (jCO) = Re W (jCO), 1l
(9.11)
Im W * (jCO) = CO Im W (jCO).1J
График
W * (jCO)
имеет вид (рисунок 9.3, а), аналогичный
W (jCO), когда в
выражениях Q(p) и R(p) разность степеней п- т >1. Если же разность степе-
ней
n m = 1, то конец графика
W * (jCO)
будет на мнимой оси ниже начала ко-
ординат (рисунок 9.3, б).
Преобразуем левую часть неравенства (9.10):

 Re(1 + jCO h) W (jCO) + 1 = Re W (jCO) CO h Im W (jCO) + 1.
Re(1 + jCO h) W (jCO) + 1 = Re W (jCO) CO h Im W (jCO) + 1.
k k
Тогда, положив
W * (jCO) = U * (CO)+ jV * (CO)
и использовав соотношения (9.11), получим вместо (9.10) для теоремы В. М. Попова условие
при всех CO z 0.
U * (CO) hV * (CO) + 1> 0
 k
k
(9.11)
Очевидно, что равенство
 U * (CO) hV * + 1 = 0
U * (CO) hV * + 1 = 0
k
(9.12)
представляет уравнение прямой на плоскости W * (jCO).
Отсюда вытекает следующая графическая интерпретация теоремы В. М. Попова: для установления устойчивости нелинейной системы доста-
точно подобрать такую прямую на плоскости
W * (jCO), проходящую через
точку
(1, j 0), чтобы вся кривая
 k
k
W * (jCO)
дежала справа от этой прямой
(рисунок 9.4).

Рисунок 9.4 – Графическая интерпретация теоремы В.М. Попова
Основная литература: 3 [324-348].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Условия абсолютной устойчивости нелинейных систем.
2. Какую устойчивость называют абсолютной устойчивостью.
3. Частотный метод В.М.Попова.
4. Критерий В.М.Попова.
Конспект лекции № 10
Тема лекции: 10 Устойчивость процессов в нелинейных САР.
В нелинейных системах в ряде случаев представляет интерес опре- деление устойчивости не только положения равновесия, но также и опре - деленны х проц ессо в, поско льк у в общем сл учае устойчивость равнове- сия в нелинейной системе может и не совпадать с устойчивостью процесса. Я. 3. Цыпкин показал, что критерий Попова может быть распространен и на исследование устойчивости процессов.
Определим условия абсолютной устойчивости вынужденного процесса в нелинейной системе, определяемого выражением
xB (t) =
f (t)
t
|
(t ¢Ñ)Ô x
(¢Ñ)] d¢Ñ. (10.1)
Путем соответствующей замены переменных в интеграле выражение
(10.1) можно представить в виде
xB (t) =
f (t)
f kИ
(¢Ñ)Ô x
(¢Ñ)] d¢Ñ
(10.2 а)
|
системе приложено исчезающее воздействие
f 1 (t). Тогда
f 1 (t)
налагается на
действовавшее ранее f(t), а процесс хв(t) также получает вариацию
(t):
xB (t) + (t) =
f (t) + f 1
(t)
t
|
(t ¢Ñ)Ô x
(¢Ñ) + (¢Ñ)] d¢Ñ
(10.3)
Из уравнения (10.3), выражающего возмущенный процесс, вычтем уравнение (10.1) вынужденного процесса и получим уравнение для отклоне- ния:
(t) =
f 1 (t)
t
f k И
(t ¢Ñ)Ô 0
(¢Ñ), ¢Ñ ] d¢Ñ, (10.4)
где
|
l0,
|
¢Ñ z 0,l
|
(10.5)
Учитывая (10.5) и (10.2 а), уравнение (10.4) представим в таком виде:
(t) =
f 1 (t)
t
f kИ
(t ¢Ñ)Ô0
(¢Ñ), ¢Ñ ] d¢Ñ, (10.6)
Это уравнение отличается от уравнения, для которого был выведен кри-
терий Попова, тем, что функция Ô 0
теперь зависит явно от времени - нелиней-
ный элемент обладает нестационарной характеристикой.
Доказано следующее условие: для того чтобы процесс в нелинейной системе, вызванный ограниченным внешним воздействием, был абсолютно ус- тойчив, достаточно, чтобы при заданном r преобразованная линейная часть
была устойчива и чтобы частотная характеристика линейной части удовлетворяла условию
W (jCO)
W (jCO) 1
(0:: CO -< 00), (10.7)

 Re + z 0 1 + rW (jCO) K r
Re + z 0 1 + rW (jCO) K r
а производная нелинейной характеристики
Ô(x)
принадлежала бы полосе
(r +,
K), т. е.
r +:: d Ô(x):: K,
 dx
dx
(10.8)
где - сколь угодно малая положительная величина.
В случае, если линейная часть (непреобразованная) устойчива, пола-
гаем
r = 0 и получаем
Re W (jCO) + 1 z 0
 K
K
(0:: CO -< 00)
или
Re KW (jCO) + 1 z 0.
Геометрически это означает, что характеристика разомкнутой линеаризо-
ванной системы
KW (jCO), которая получается из исходной нелинейной системы
в результате замены нелинейного элемента линейным с коэффициентом пере-
дачи К, должна лежать правее прямой
V (CO) = 1, или же характеристика
W (jCO)
должна лежать правее прямой, V (CO) = 1/ K
(рисунок 5.11).

. Рисунок 10.1 Рисунок 10.2. Новел системе коодинат Характеристика разомкнутой
линеаризованной системы
При этом характеристики нелинейного элемента должны удовлетворять ус- ловиям
0 -<
Ô x (t) + (t)] Ô x (t)]
(t)
-< K,
(10.9)
т. е. характеристика должна лежать в секторе (01, K 1) новой системы коор-
динат (рисунок 10.2). Очевидно, наклон
 d Ô1()
d Ô1()
01 K 1
равен наклону ОК. Если
0 -<
d ()
-< K, это условие выполняется. В общем случае, когда разомкнутая
линейная система неустойчива или нейтральна и r отлично от нуля, имеем
KW (j CO )
1
(10.10)
Re + z 0,
A + KW (jCO) A 1
где обозначено
A = K.
 r
r
Пусть
KW (jCO) = U + jV. Тогда, заменяя неравенство (5.65) равенством, по-
лучаем уравнение границы области, внутрь которой не должна входить ха-
рактеристика
KW (jCO):
U + jV 1
+ = 0,
A + U + jV
A 1
что можно привести к виду
(

A + 1\

+ V 2 = (A 1\.
(10.11)
касания (1,
j 0).

Рисунок 10.3 Рисунок 10.4 Геометрическая интерпретация критерия Геометрическая интерпретация абсолютной устойчивости
Нетрудно видеть, что семейство окружностей получается примерно та- ким, какое мы получали в ч. I при построении круговых диаграмм для равных значений ординат вещественной частотной характеристики замкнутой систе- мы.
Теперь можно дать следующую геометрическую интерпретацию крите- рию абсолютной устойчивости процессов в общем случае: для того чтобы про- цессы в нелинейной системе при ограничен них воздействиях были абсолютно устойчивы, достаточно, чтобы производная от характеристики нелинейного
элемента
d Ô / dx
принадлежала полосе (r +,
K), где — сколь угодно малая
положительная величина, и чтобы частотная характеристика линеаризо-
ванной разомкнутой системы
KW (jCO), удовлетворяя частотному крите-
рию Найквиста, находилась вне соответствующей А-окружности (риу-
нок10.3), или же чтобы характеристика
W (jCO)
лежала вне окружности,
пересекающей ось абсцисс в точках
1/ K - и
1/ r
(рису но к, 10.4).
Основная литература: 3 [324-348].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Устойчивость процессов в нелинейных САР.
2. Условие абсолютной усточивости вынужденного процесса в нелинейной сис- теме.
3. Частотный критерий Найквиста.
Конспект лекции №11
Тема лекции: 11. Основные понятия о фазовой плоскости.
Метод изображения переходных процессов в фазовом пространстве, в фазовой плоскости был введен в теорию регулирования академиком Л. Л. Ан- дроновым. Им был решен ряд классических задач теории регулирования, в том числе задача Вышнеградского с учетом сухого трения в регуляторе.
Метод дает возможность получить наглядную н точную картину всей совокупности переходных процессов при любых начальных условиях для свобод- ных колебаний в системах второго порядка, содержащих нелинейные элементы. А. А. Андронов решил одну из задач для уравнений третьего порядка. Большое
количество задач построения «фазовых портретов» различных нелинейных систем было решено В. В. Казакевичем, В. В. Петровым и Г. М. Улановым и рядом других авторов.
Хотя исследование систем второго порядка для теории регулирования имеет ограниченный интерес, знакомство с основами метода фазовой плос- кости весьма полезно благодаря его исключительной наглядности и изяще- ству.
Фазовой плоскостью называется плоскость, в которой по осям коор- динат откладываются какие-либо две переменные, характеризующие пе- реходный процесс в системе. Наиболее часто в качестве таких переменных принимают отклонение регулируемой величины х и скорость ее изменения по времени
 dx = y dt
dx = y dt
(11.1)
При изображении процессов на фазовой плоскости уравнение второго по- рядка удобно свести к двум уравнениям первого порядка:
 dx =
dx =
dt
dy
f (x, y), l
(11.2)
dt = f 2 (x, y),1J
где
f 1 и
f 2 - в общем случае нелинейные функции координат. Чтобы изобра-
зить переходный процесс на фазовой плоскости, из уравнений (11.2) исклю- чим время, для чего поделим второе уравнение на первое:
 dy =
dy =
dx
f 2 (x, y). (11.3)
 f 2 (x, y)
f 2 (x, y)
Мы получили нелинейное дифференциальное уравнение, общих мето- дов точного решения которого не существует, и в каждой задаче приходится изыскивать частный метод его решения. Решением уравнения (11.3) будет некоторая функция
y = F (x), (11.4)
графическое изображение которой на фазовой плоскости называется ф а -
з о в о й т р а е к т о р и е и. Как известно, каждой совокупности начальных
условий
x 0,
y 0 будет соответствовать свое решение и своя фазовая траекто-
рия. Фазовая плоскость для каждого уравнения покрывается множеством фа- зовых траекторий, однако это множество обладает весьма ценным свойством:
если функции
f 1и
f 2 однозначны, то каждой точке (х, у) на плоскости (за
исключением, может быть, ограниченного числа изолированних особых точек) соответствует только одно значение производной dy/dx. Это означает, что через каждую точку фазовой плоскости (за исключением особых точек) проходит только одна фазовая траектория и что фазовые траектории не пе- ресекаются друг с другом. Данное обстоятельство и позволяет получать на- глядные «фазовые-портреты» исследуемой системы, на которых ясно виден характер возможных движений, подобно тому, как с помощью магнитных силовых линий получаем наглядное представление о магнитном поле.
Однако многие нелинейности характерны тем, что при возрастании
координаты, т. е. при
x > 0, движение происходит по одной ветви кривой, а
при ее убывании, т. е. при
x -< 0, по другой. Тогда, хотя характеристика эле-
мента неоднозначна, на фазовой плоскости будем иметь опять-таки непересе-
кающиеся фазовые траектории, так как области
x > 0 и
x -< 0
разграничены
осью абсцисс
y = x = 0, которую можно при этом назвать линией переключе-
ния, поскольку на этой оси происходит переход фазовой траектории, опреде- ляемой одним уравнением, на траекторию, описываемую другим уравнени- ем.
И лишь в том случае, если неоднозначность является более сложной, может оказаться, что в точках некоторых областей фазовой плоскости будут пересе- каться несколько фазовых траекторий. В этом случае прибегают к понятию многолопастных фазовых плоскостей.
Мы упомянули о том, что однозначность фазовых траекторий, прохо- дящих через данную точку, может не иметь места в так называемых «особых точках». Эти особые точки представляют собой те точки, в которых проис-
ходит одновременное обращение в нуль функций
f 1 и
f 2:
|
(11.6)
Особые точки, определяемые решением системы уравнений (11.5),
отмечены нами нулевым индексом вверху, чтобы отличить их от начальных
условий
x 0,
y 0, отмечаемых нулевым индексом внизу.
Заметим, что на основании (11.2) в особых точках dx/dt и dy/dt обра- щаются в нуль, т. е. движение системы прекращается. Это означает, что особые точки представляют собой точки равновесия системы. Заметим сра- зу же что эти точки могут быть как реализуемыми физически, т.е. устойчи- выми, так и нерелизуемыми, т.е. неустойчивыми, и в неустойчивых точках возможность прекращения движения существует только формально.
Мы говорили о том, что чаще всего за координату y принимают скорость изменения координаты х. Тогда уравнения (11.2) принимают вид
 dx = y, l
dx = y, l
dt 1
dy
(11.6)
dt J
Фазовые траектории при этом приобретают некоторые дополнительные свойства. Прежде всего, из уравнений (11.6) следует, что х всегда возрас-
тает в верхней полуплоскости (где
y > 0), т. е. движение вдоль фазовой тра-
ектории при возрастании t происходит слева направо. В нижней же полу-
плоскости (где
y -< 0) координата х убывает, и движение по фазовой траекто-
рии происходит справа налево.
Следующее интересное свойство вытекает из уравнения (11.3), которое в данном случае принимает вид
dy f
(x, y)

 =. (11.7)
=. (11.7)
dx y
При у= 0 величина dy/dx становится бесконечно большой во всей фазовой плоскости, за исключением точек равновесия, где f(х, у) = 0. Это означает, что в точках пересечения фазовых траекторий с осью х касательные к фазовым траекториям перпендикулярны к оси х.
Хотя метод фазовых траекторий разработан, применительно к нели- нейным системам, представляет интерес сначала рассмотреть фазовые тра- ектории колебательного линейного звена второго порядка, так как на ней можно легко проследить получение фазовых траекторий и особых точек наиболее важных типов, которые встречаются и нелинейных системах.
Фазовое пространство
Для наглядного представления о сложных нелинейных процессах регули- рования часто прибегают к понятию фазового пространства, которое заключа- ется в следующем. Дифференциальное уравнение замкнутой системы регу- лирования n -го порядка можно преобразовать к системе п дифференциаль- ных уравнений первого порядка в виде

 dx 1 dt dx 2
dx 1 dt dx 2
dt
= Ô1(x 1, x 2,..., xn,
= Ô 2 (x 1, x 2,..., xn,
f, g) l
(11.8)
............................................. 1
 dxn
dxn
dt
= Ô n (x 1, x 2,..., xn,
f, g)1
1J
с начальными условиями
x 1= x 10,
x 2= x 20,..., xn = xn 0
при
t = 0,
где
x 1, x 2,..., xn- переменные, являющиеся искомыми функциями времени, при-
чем
xi может обозначать регулируемую величину,
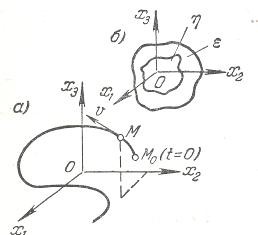
Рисунок 11.1. Трехмерная система
а x 2,..., xn
- вспомогательные переменные; f и g возмущающее и задающее
воздействия.
Пусть, например, в уравнениях (11.8) будет п= 3 (система третьего по- рядка). Переменные x 1, х 2, х 3 здесь могут иметь любой физический смысл. Но условно их можно представить мысленно как прямоугольные координаты некоторой точки М (рисунок 11.1, а).
Дата добавления: 2015-08-20; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Конспект лекции №1 3 страница | | | Конспект лекции №1 5 страница |