|
Читайте также: |
k 1предпочтительнее вычислять по выражению
ò о
k = M y х / cr 2,
(4.5)
1 x
L J
где М-символ математического ожидания.
Если
x (t), то
ô (x) -одномерная функция плотности распределения вероятности
my =
f ô (x) f (x) dx;
|
(4.6)
cr x
{ f 2 (x) ô (x) dx m 2}0.5;
(4.7)
|
= 1
cr 2
f(x mx) f (x) ô (x) dx;
(4.8)
x 00
здесь (1) и (2) у
k 1 относятся к первому (4.4) и второму (4.5) способам вычисле-
ния
k 1.
Расчеты показывают, что при выборе
k 1по первому и второму способам в
корреляционной функции выходного сигнала получаются односторонние
ошибки разных знаков, поэтому в качестве
k 1целесообразно использовать
(1)
(2)]/ 2.
k 1= k 1
+ k 1
(4.9)
Совместная гармоническая и статистическая линеаризация. Часто
входной сигнал
z (t) нелинейного звена представляют суммой синусоидального
сигнала и случайной функции
x (t):
о
z (t) = A sin wt + x (t) = A sin wt + m x + х (t).
(4.10)
В этом случае применяют совместную гармоническую и статистическую
линеаризацию, т.е. заменяют характеристику нелинейного звена приближенной
y (t) =
f z (t)]
y (t) �
о
f 0 + 1 A cos wt + 2 A cos wt + х (t),
(4.11)
линейной относительно синусоидальной и центрированной случайных состав- ляющих входного сигнала.
При нечетной характеристике
y = f (z)
f 0= 0 mx.
(4.12)
Значения
0,1,2
и можно определить различными способами из усло-
вия правильного учета передачи нелинейным звеном полезного сигнала, пер- вой гармоники и уровня флюктуации входного сигнала.
Предположим, что mx
и cr 2 изменяются достаточно медленно и их можно
|
y (t) �
о
|
|
(4.13)
|
|
|
входного сигнала значения
0 k 1оказываются периодическими функциями
времени, следовательно к ним можно применить гармоническую линеаризацию
|
|
f 0(mx + A sin wt, cr x) �
f 0(A, mxcr x) +1(A, mx, cr x) A sin wt + 2(A, mx, cr x) A cos wt,
(4.14)
где
1 2 ï
|
2 ï
f f 0(mx + A sin, cr x) d
(4.15)
1 2 ï
|
(4.16)
1 2 ï
|
(4.17)
k = (A, m, cr) � 1
1 x x 2 ï
2 ï
f k 1(mx + A sin, cr x) d
(4.18)
= COt
Если известна
ô (x)
- одномерная функция плотности распределения ве-
роятности, то на основании предыдущего раздела о статистической линеариза- ции имеем
f * =
f f (x + A sin) ô (x) dx;
0.5 00
(4.19)
l
k = 1 k (1) + k (2) ]= 1 1
ò
cr 1 f f 2(m
+ А sin) ô (x) dx (f *)2
1 1
+ 
|
|
(4.20)
1 2 1 1
í±
21l
x x
L 00
0 cr 2
x
dx
1J
Основная литература: 1 [210 - 220].
Дополнительная литература: 1 [365 - 414].
Контрольные вопросы:
1. Метод гармонического баланса.
2. Гармонические коэффициенты передачи некоторых нелинейных элементов.
3. Изменение входной величины нелинейного элемента
Конспект лекции 5
Тема лекции: 5. Исследование нелинейных систем. Метод гармонического баланса и статистической линеаризации
Метод гармонического баланса позволяет оценить устойчивость нели- нейных систем, определить амплитуду и частоту автоколебаний, а также вы- брать корректирующие цепи, обеспечивающие заданные характеристики нели- нейных систем. Возможность применения этого метода к стационарным систе- мам определяется близостью периодического движения системы к гармониче- скому. Это условие обычно удовлетворяется, когда линейные части системы являются фильтрами низких частот, т.е. хорошо отфильтровывают высокие гармоники.
Предположим, что нелинейная система состоит из линейной части с ком-
плексной частотной функцией
Wë (jCO)
и нелинейного безынерционного звена с
комплексным гармоническим коэффициентом усиления
Wí (A). Пусть в этой
системе возникли автоколебания с частотой COa и амплитудой критерию Найквиста
Aa, тогда согласно
Wл (jCO) Wн (A) = 1, (5.1)
или, обозначив
|
|
(5.2)
условия возникновения автоколебаний запишем в виде
M л (jCO) = Wн (jCO).
(5.3)
Для определения частоты
COа
и амплитуды
Аа автоколебаний решение
(5.3) удобно проводить графически. Для этого построим (рисунок 5.3, а) в ком-
плексной плоскости
Wл (jCO) и
- M н (A). если они пересекаются, то в системе
возможны автоколебанбия, если не пересекаются, то автоколебания невозмож-
ны. Параметры автоколебаний
COa и
Аа определяются точкой пересечения
Wл (jCO)
и M н (A): COа по Wл (jCO) и
Аа по
- M н (A).
Если
Wл (jCO)
и M н (A) пересекаются в нескольких о то как рисунок 5.2 б,
то это свидетельствует, что в системе возможны автоколебания с различными
параметрами
(CO и
A).
Определение устойчивости автоколебаний производится по следующему
правилу: если Wл (jCO)
при изменении CO от 0 до 00 охватывает часть
- M н (A),
соответствующую увеличению амплитуды, от автоколебания неустойчивые, в неустойчивые, в противном случае- устойчивые.
Рисунок 5.1. Графический метод определения параметров автоколебаний в не- линейной систем
Руководствуясь этим правилом, можно заключить, что из трех автоколе- баний на рисунке 5.1, а и б устойчивым будут только автоколебания в первой
точке на рисунке 5.1, б с параметрами COa 1и
Aa 1.
Метод статистической линеаризации. Рассмотрим нелинейную систе- му, изображенную на рисунке 5.2, где <ð - нелинейное звено с характеристикой
z = <ð (y), (5.4)
W (p) - передаточной функция линейной части системы.
x (t)
с ма-
тематическим ожиданием
mx и дисперсией
cr x. Необходимо определить харак-
теристики выходного сигнала
y (t): математическое ожидание my
и дисперсию
(5.4)
Произведем статистическую линеаризацию нелинейной характеристики
z (t) = k 0 my + k 1 y (t), (5.5)
где коэффициенты
k 0 и
k 1 в общем случае являются известными функциями
пока неизвестных величин
my и cr y:
k 0= k 0(my, cr y);
k 1= k 1(my, cr y);
(5.6)
Таким образом, в результате статистической линеаризации нелинейное звено заменяется безынерционным усилителем с различными коэффициентами
усиления полезного сигнала
my и помехи
y (t). Передаточные функции линеа-
ризованной системы для полезного сигнала и помехи имеют вид
|
y
(p) = W (p) / 1 + k 0 W (p)];
(5.7)
|
y
(p) = W (p) / 1 + k 1 W (p)].
(5.8)
С использованием (5.7) при
mx = const
m = m W (0)/ 1+ k (m, cr
) W (0)].
(5.10)
y x 0 y y
Уравнение (5.10) содержит две неизвестные величины
(my
и cr y) и
поэтому может быть решено только совместно с уравнением, определяющим дисперсию выходной величины,
|
f S x
ò
(CO)
W (jCO)
dCO,
(5.11)
2 ï 00
L1 + k 1 (my, cr y) W (jCO) J
х + W (p) y
– z
Woc (p)
Рисунок 5.2. Нелинейная АСР
где
S x (CO)
спектральная плотность
x (t).
Уравнения (5.10) и (5.11) могут быть решены совместно методом последовательных приближений. Для этого необходимо задать исходные
приближенные значения
k 0 и
k 1и вычислить в первом приближении
my и
cr y по
(5.10) и (5.11). После этого можно уточнить значения
k 0 и
k 1и вычислить
my и
cr y
во втором приближении и т.д.
Уравнения (5.10) и (5.11) можно решить графическим методом. Для этого
заменим (5.10) равноценной системой уравнений
= my;
(5.12)
= mxW (0) /[1 + k 0(my, cr y) W (0)].
(5.13)
Уравнению (5.12) соответствует биссектриса координатного угла на
рисунке 5.3, a в координатах
my; в этих же координатах уравнению (5.13)
соответствует семейство кривых с параметром
cr y, построив кривые, соответст-
вующие (5.13) для ряда значений
cr y
и определив точки пересечения их с пря-
мой (5.12), найдем значения
myi, соответствующие
cr y
выбранным значениям
cr yi. После этого по найденным точкам построим кривую 1 (рисунок 5.3, б) в
координатах
mycr y. В этих же координатах построим кривую 2 по уравнению
(5.11). Точка А пересечения кривых 1 и 2 дает искомое решение.
Изложенный метод применим только к системам, где невозможны авто-
колебания, так как только при их отсутствии
my может быть постоянной вели-
чиной при постоянном
mx. Поэтому прежде чем применять изложенный метод,
необходимо исследовать систему на возможность возникновения в ней автоко- лебаний, что можно сделать методом гармонического баланса. Если исследова- ние покажет, что в системе возможны устойчивые автоколебания, то для опре- деления ее точности необходимо применять метод совместной статической и гармонической линеаризации.
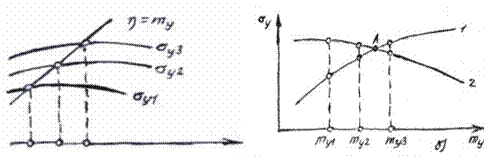
а) б)
Рисунок 5.3. Графическое решение уравнений (5.10) и (5.11)
Основная литература: 1 [210-220].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Статистическая характеристика нелинейного элемента.
2. Математическое ожидание нелинейной функции.
3. Расчет нелинейных систем методом статистической линеаризации.
Конспект лекции № 6
Тема лекции: 6 Метод фазовых траекторий
Метод фазовых траекторий. Состояние динамической системы, описы-
ваемое дифференциальными уравнениями
n го порядка, в каждый момент
времени определяется значениями регулируемой величины и
(n 1)
ее произ-
водных. Это дает возможность представить в некотором
n мерном простран-
стве состояние системы в каждый момент времени отдельной точкой- так назы- ваемой изображающей точкой. Процесс изменения состояния системы пред- ставляется как некоторое движение изображающей точки, точнее – как ее тра- ектория, так называемая фазовая траектория. Совокупность фазовых траекто- рий составляет фазовую картину системы (фазовый портрет системы).
Для практических расчетов пользование многомерным фазовым про- странством связано с определенными трудностями, поэтому при анализе нели- нейных систем обычно ограничиваются двухмерной фазовой плоскостью. В этом случае по оси абсцисс откладывают значение регулируемой величины у
(ее отклонение от установившегося состояния), а по оси ординат – значение
z = dy / dt.
Состояние АСР, описываемое управлением не выше второго порядка, в каждый момент времени определяется значениями y и z и может быть охарак- теризовано положением точки M на фазовой плоскости (рисунок 6.1). в пере- ходном процессе значения y и z будут изменяться и, следовательно, изобра- жающая точка M будут занимать различные положения на фазовой плоскости. По траектории этой точки можно судить о характере переходного процесса.
Если y - отклонение регулируемого параметра от установившегося зна-
чения, то для устойчивых систем в установившемся состоянии
y = 0 и
z = 0,
следовательно, фазовые траектории устойчивой АСР при
t í 00 должны стре-
миться к началу координат, а фазовые траектории неустойчивой АСР при t í 00 должны удаляться от начала координат. Точки фазовой плоскости, где сходится (или откуда расходятся) фазовые траектории, называется особыми точками.
Рисунок 6.1. Характеристики состояния динамической системы:
а во временной области; б
на фазовой плоскости
В параметрической форме фазовые траектории описываются системой уравнений
dy dt = P (y, z):l
|
(6.1)
где
P (y, z)
и Q (y, z) нелинейные функции y и z.
Разделив второе уравнение системы (6.1) на первое, получим дифферен- циальное уравнение фазовой траектории.
dz dy = Q (y, z) / P (y, z) = H (y, z).
(6.2)
Разделив переменные и проинтегрировав (6.2) получим выражения для семейства фазовых траекторий. Для определения устойчивости АСР следует рассматривать поведение фазовых траекторий в окрестностях особых точек (в данном случае – в окрестности начала координат). Для этой цели линеаризуем систему уравнений (6.1), т.е. разложим их в ряд Маклорена, и ограничимся двумя первыми членами, в результате получим
dy dt = ay + bz;
(6.3)
dy dt = cy + bz, (6.4)
где
a = ä P
ä y;
b = ä P
ä z;
c = ä Q
ä y;
d = ä Q
ä y;
при
y = z = 0.
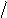Решив (6.3) и (6.4) относительно y, получим линеаризованное уравнение движения системы в окрестностях особой точки:
y,,(a + b) y, + (ad bc) y = 0. (6.5)
Поведение системы в окрестностях особой точки определяется корнями характеристического уравнения
p 2 (a + b) p + (ad bc) = 0
(6.6)
Например. если корни уравнения мнимые, т.е.
p 1.2= ± jCO, то
y (t) = A cos COt;
(6.7)
z (t) = y (t) = ACO sin COt.
(6.8)
Возведя в квадрат (6.7) и (6.8) и сложив, получим уравнение фазовых тра- екторий в виде
y 2 / A 2+ z 2 / A 2 CO 2 = 1.
(6.9)
Это – уравнение эллипса. Переходной процесс и фазовая траектория для этого случая изображены на рисунок 6.2. особой точкой, которая носит название центр, здесь является начало координат.
Отметим, что незатухающим колебаниям
y (t)
(автоколебаниям) на фазо-
вой плоскости соответствуют фазовые траектории в виде эллипсов; другим словами, наличие замкнутых фазовых траектории на фазовой плоскости свиде- тельствует о возможности возникновения автоколебаний в АСР.
Различные случаи особых точек, их названия, соответствующие им пере- ходные процессы и фазовые траектории приведены в таблица 6.1, где 1-3- раз- личные переходные процессы и соответствующие им фазовые траектории на фазовой плоскости.
Приведенные в талблица 6.1 фазовые траектории справедливы только
для определенной области
y z, в которой допустима линеаризации системы
уравнений (6.1). За пределами этой области в силу существенного отхода от линейных соотношений в исходных временных уравнениях фазовые траекто- рии будут иметь качественно иной характер. Для тех нелинейных АСР, у кото-
рых статистические характеристики нелинейных звеньев могут быть разбиты на линейные участки, можно построить фазовые траектории отдельно для каж- дого линейного участка, а затем соединить (припасовать) их друг с другом.
a) б)
Рисунок 6.2. Переходный процесс (а) и фазовая траектория
(б) для автоколебаний
Рисунок 6.3 – Построение фазовых траекторий методом изоклин
Таблица 2.1
Особые точки
| Название | Переходный | Фазовые траектории |
| Устойчивый фокус |
|
|
| Неустойчивый фокус |
|
|
| Устойчивый узел |
|
|
| Неустойчивый узел |
|
|
| Седло |
|
|
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Основные понятия о фазовой плоскости.
2. Что такое фазовая плоскость?
3. Что такое фазовая траектория?
4. Что такое фазовое пространство?
Конспект лекции №7
Тема лекции: 7 Построение фазовых траектории методом изоклин предель- ные циклы
Дата добавления: 2015-08-20; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Конспект лекции №1 1 страница | | | Конспект лекции №1 3 страница |
