Конспект лекции №1 1 страница

Тема лекции: 1. Особенности нелинейных систем и нелинейные характери- стики

Особенности нелинейных систем

Нелинейной называется система, для которой не выполняется принцип суперпозиции [1]. Поведение такой системы описывается нелинейными диффе- ренциальными уравнениями. На практике наиболее часто встречаются системы с безынерционными нелинейными звеньями. Оператором преобразования тако- го звена является функциональная зависимость между входной и выходной ве- личинами, называемая статической характеристикой звена.

Нелинейным АСР присущи принципиально новые свойства в динамике, которые отсутствуют у линейных АСР. Обратим внимание на некоторые из них.

Во-первых, к нелинейным АСР, как указывалось выше, неприменим принцип суперпозиции. Во - вторых, качество переходных процессов в нели- нейных АСР зависит от величины возмущения. На рисунок 1.1 иллюстрируется характер переходных процессов в одной и той же нелинейной системе при раз- личных возмущениях.

Отличительной особенностью нелинейных систем является возможность возникновения в них автоколебаний. На рисунок 1.2 а показан

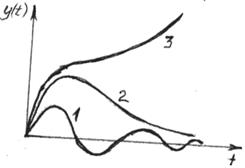
Рисунок 1.1. Переходные процессы при различных возмущениях:

1- колебательная устойчивость; 2- апериодическая устойчивость; 3 - неустойчивый процесс

случай, когда при любых возмущениях в системе устанавливаются незатухаю- щие колебания с постоянной амплитуды. Такие устойчивые колебания с посто- янной амплитудой называются автоколебаниями. Автоколебания представляют собой новый вид установившегося режима, возможного при отсутствии внеш- них возмущений и характерного только для нелинейных систем. На рисунок 1.2 б показан случай, когда амплитуда установившихся колебаний зависит от сте- пени возмущения. На рисунок 1.2 в показан случай, когда при малых возмуще- ниях автоколебания устойчивые, а при больших возмущениях-неустойчивые.

Таким образом, при указанных особенностях нелинейных систем необхо- димо при рассмотрении устойчивости оговаривать начальные условия и внеш- ние воздействия. Поэтому для нелинейных систем надо говорить не об устой-

чивости вообще, а об устойчивости определенного их режима. В связи с этим при изучении нелинейных систем употребляют понятия устойчивости в малом, в большом и в целом.

Устойчивость в малом – это устойчивость при бесконечно малых откло- нениях от исходного режима. Устойчивость при конечных отклонениях, воз- можных в данной системе по условиям ее работы. Устойчивость в целом – это устойчивость при отсутствии каких-либо ограничений на отклонения.

Нелинейные характеристики

Большинство встречающихся на практике нелинейных статических ха- рактеристик

а)

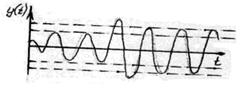
б)

в)

Рисунок 1.2. Различные виды автоколебаний в нелинейных системах

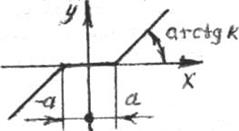
Рисунок 1.3. Характеристика типа «нечувствительность»

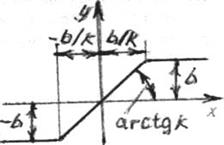
Рисунок 1.4. Характеристика типа «ограничение»

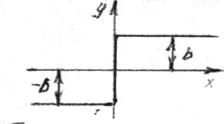
Рисунок 1.5. Идеальная релейная характеристика

y = f (x)

может быть сведено к типовым, рассмотренным ниже, и разделено на

две группы: однозначные и неоднозначные. Однозначной статической харак- теристикой называется такая, вид которой не зависит от направления измене- ния входной величины х нелинейного звена. Вид неоднозначной статической характеристики зависит от направления изменения входной величины х: при

увеличении

x [ dx / dt)0]

выходная величина у изменяется по одной зависимости

от входной, при уменьшении

x [ dx / dt <0] -по другой.

n

Однозначные нелинейные статические характеристики. При матема- тическом описании однозначные нелинейные статические характеристики мо- гут быть представлены в виде непрерывных и разрывных функций от х. Непре- рывные нелинейные характеристики чаще всего определяются в виде полинома степени п для определенного диапазона изменения х:

y = a 0

x n + a x n 1+... + a

при

b < x < c, (1.1)

где

ai -постоянные коэффициенты, b и

c (b < c)-диапазон изменения х.

Разрывные характеристики могут быть сведены к различным комбинаци- ям из четырех приведенных ниже типовых характеристик:

Рисунок 1.6. Релейная характеристика с зоной нечувствительности

Рисунок 1.7. Характеристика типа «люфт»

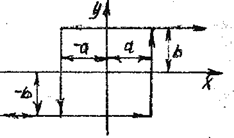
Рисунок 1.8. Двухпозиционная релейная характеристика с зоной нечувстви- тельности

Рисунок 1.9. Трехпозиционная релейная характеристика с зонами нечувстви- тельности

нечувствительность (рисунок 1.3):

y = 0

при

х < а; l

у = k(x - a)

J

при х > а;

(1.2)

у = k(x - a)

при х < а; 1

ограничение (рисунок 1.4):

y = kx

при

х < b/k; l

1

y = b

при х > b/k;

(1.3)

y = -b

при х < -b/k;1

J

идеальная релейная характеристика (рисунок 1.5):

y = b y = -b

при х > 0;l

J

при х < 0;

(1.4)

релейная с зоной нечувствительности (рисунок 1.6):

y = 0

при

х < а; l

1

у = b

у = b

при х > а;

J

при х < а; 1

(1.5)

Неоднозначные нелинейные статические характеристики. Наиболее распространенные типовые разрывные характеристики приведены ниже:

л юфт (рисунок 1.7):

у = k(x - a)

у = k(x + a)

при dx / dt > 0; l

при dx / dt < 0; 1

1

(1.6)

dy / dx = 0

при y/k x < a; J

двухпозиционная релейная характеристика с зонами нечувствительно- сти (рисунок 1.8):

y = b y = -b

y = b

при х > а;l l

если dx/dt > 0; 1

при х < а;J 1

при х > а; l

(1.7)

если dx/dt < 0;1

y = -b

при х < а;J J

т рехпозиционная релейная характеристика с зонами нечувствительно- сти (рисунок 1.9):

y = b

при x > a 2; l l

1 1

y = -b

при х < -а1;

если dx/dt > 0; 1

y = 0

при - а1

< х < а 1 11

2 J

(1.8)

y = b

при

x > a 1; l 1

y = b

при х < -а;

1 если dx/dt < 0.1

1 1

y = 0

при - а

< х < а, 1 1J

2 1 J

Основная литература: 4 [599-610].

Дополнительная литература: 1 [365-414].

Контрольные вопросы:

1. Нелинейные системы и элементы.

2. Звено релейного типа.

3. Звено с кусочно-линейной характеристикой.

4. Класс нелинейных систем.

5. Какие системы автоматического регулирования называются нелинейными?

6. Какие виды нелинейных элементов Вам известны?

Конспект лекции № 2

Тема лекции: 2. Линеаризация нелинейных характеристик путем разложе- ния в ряд

Разработанные в настоящее время точные методы исследования нелиней- ных АСР практически могут применяться для систем, описываемых нелиней- ными дифференциальными уравнениями невысокого порядка, и часто сложны для инженерного использования. Поэтому в инженерной практике большое применение находят приближенные методы, основанные на замене действи- тельных зависимостей между входной и выходной переменными приближен- ными линейными. При этом линеаризацию необходимо производить так, чтобы учесть хотя бы приближенно нелинейные свойства звеньев, т.е. чтобы для ли- неаризованных элементов не выполнялся принцип суперпозиции.

Линеаризация нелинейных характеристик путем разложения в ряд

состоит в замене характеристики

y = f (x)

приближенной линейной зависимо-

стью, определяемой двумя первыми членами разложения характеристики в ряд

Тейлора. Пусть характеристика

y = f (x)

дифференцируема и входной сигнал

x (t)

y =

мало отличается от некоторого среднего значения

'

f (x) можно заменить приближенной

x 0, тогда зависимость

y = f (x 0

)+ f

(x 0)(x x 0),

(2.1)

Замена нелинейной зависимости

y = f (x)

линейной (2.1) геометрически

представляет собой замену кривой

y = f (x), касательной к ней в точке

x 0.

Действующие в АСР внешние возмущения можно представить как ста-

ционарные случайные функции

x (t)

с математическим ожиданием mx

о

и центри-

рованной случайной составляющей

х (t):

x (t) = mx + x (t)

(2.2)

В этом случае практически линеаризацию нелинейной характеристики целесообразно производить относительно центрированного входного случайно-

го сигнала

x (t), т.е. за центр разложения

x 0 в (2.1) взять математическое ожида-

ние mx

входного сигнала

x (t). В результате получается

y (t) �

f (mx) + f

(mx) x (t)

(2.3)

'

Таким образом, приближенная зависимость (2.3) линейна только относи-

о

тельно случайной составляющей

тельно математического ожидания неприменим.

x (t) входного сигнала и нелинейна относи-

mx, поэтому принцип суперпозиции здесь

Основная литература: 4 [600-620].

Дополнительная литература: 1 [365-414].

Контрольные вопросы:

1. Метод решения задачи, методом припасовывания.

2. Как определяется амплитуда найденных автоколебаний?

Конспект лекции № 3

Тема лекции: 3. Линеаризация нелинейных характеристик. Метод гармони- ческой линеаризации

В целом ряде практических задач приходится рассматривать воздействие на линейное звено гармонических колебаний

x (t) = Àsin wt

= Àsin;

= wt.

(3.1)

Выходной сигнал нелинейного звена также будет периодическим, но не гармоническим. В качестве примера на рисунок 3.1 приведены графики сигна-

лов

y (t) на выходе нелинейных звеньев с различными характеристиками.

Идея гармонической линеаризации состоит в том, что выходные перио-

дические колебания

y (t) разлагают в ряд Фурье и для дальнейших исследований

ограничиваются рассмотрением лишь первых гармоник

а) б)

Рисунок 3.1. Сигнал (а) на выходе нелинейного звена с характеристикой (б)

этого ряда. В этом случае нелинейная зависимость ется приближенной

y = f (x) =

f (Àsin) заменя-

y (t) = a 0+ a sin wt + b cos wt

= a 0+ q 1 x + q 2 x / w,

(3.1)

где

a = 1

0 2 ï

2 ï

f f (Àsin) d;

(3.2)

1 2 ï

q 1= ï Àf f (Àsin)sin d;

(3.3)

1 2 ï

q 2 = ï Àf f (Àsin) cos d;

(3.4)

Коэффициенты

q 1 и

q 2называются гармоническими коэффициентами

усиления нелинейного звена, они зависят от характеристики нелинейного эле-

мента и от амплитуды А входного синусоидального сигнала, т.е.

q 1= q 1(À),

q 2= q 2(À). Для типовых нелинейных характеристик формулы для вычисления

q 1 (À) и

q 2(À) приведены в таблица 3.1. Для нечетных характеристик

a 0= 0,

для

однозначных характеристик нелинейные характеристики.

q 2(A) = 0. В дальнейшем рассматриваются нечетные

Выражение (2.1) при

a 0= 0 можно представить в виде

y (t) = c À sin(wt + 8),

(3.5)

где

c = q 1
+ q 2;

0 = arctg (q 2/ q 1).

(3.6)

Часто удобно входной сигнал рассматривать в комплексной форме:

x (t) = À e jwt,

(3.7)

тогда первая гармоника выходного сигнала принимает вид

y (t) = c À e j (wt + 8).

(3.8)

Введем понятие комплексного гармонического коэффициента усиления нелинейного звена

H

тогда

W (À) = ce j8,

(3.9)

y (t) = WH (A) x (t).

(3.10)

Используя (3.6), WH (A)

можно представить в виде

WH (A) = q 1(A) + jq 2(A).

(3.11)

Коэффициент

WH (A)

не зависит от частоты входных колебаний, а зави-

сит от их амплитуды А, в этом в основном и состоит отличие нелинейного бе- зынерционного звена от линейного инерционного.

Таблица 3.1.

Коэффициенты гармонической линеаризации типовых нелинейных харак- теристик

Статическая характери- стика	q 1(A)	q 2(A)
Нечувствительность (ри- сунок 1.3)	2 k (a a a 2 \   при A > a
Ограничение (рисунок 1.4)	2 k (b b b 2 \ arcsin + 1 ï kA kA k 2 A 2
при A >	b
k
Идеальная (рисунок 1.6)	4 b ïA
Релейная с зоной нечув- ствительности (рисунок 1.6)	4 b a 2 1 при A > a ïA A 2
Люфт (рисунок 1.7)	k ò ï (2 a \ (2 a \ a (a \ + arcsin 1 + 2 1 õ 1 ï L 2 A A A A J при А > a 2	4 ka (1 a \   ïA A при A > a
Двухпозиционная релей- ная с зоной нечувстви- тельности (рисунок 1.8)	4 b a 2 1 при A > a ïA A 2	- 4 ab ïA 2 при A > a
Трехпозиционная релей- ная с зонами нечувстви- тельности (рисунок 1.9)	ò 2 2 ïA A 2 A 2 L J при A > a 2	2 a 2 b (a 1\ ïA 2 1 a при A > a 2

k ï arcsin A + A

A 2

2 b

1 a 2 +

1 a 1

Основная литература: 4 [702-712].

Дополнительная литература: 1 [301-322]; 2 [285-360].

Контрольные вопросы:

1. В чем сущность метода гармонической линеаризации?

2. Каковы ограничения применения метода гармонической линеаризации?

3. Что называется приближенной передаточной функцией и эквивалентным комплексным коэффициентом усиления нелинейного элемента?

4. Что называется комплексным коэффициентом усиления линейной части?

5. В каком порядке производится исследование нелинейной системы методом гармонической линеаризации?

Конспект лекции № 4

Тема лекции: 4. Линеаризация нелинейных характеристик статистическая линеаризация

Метод приближенной замены нелинейной характеристики эквивалент- ными в вероятностном смысле линейными зависимостями называется методом статистической линеаризации. В результате такой линеаризации нелинейная за-

висимость

y = f (x) заменяется приближенной

о

y (t) � k 0 mx + k 1 x (t),

(4.1)

где

mx = const -математическое ожидание стационарного случайного сигнала на

входе нелинейного элемента; x (t) -центрированная случайная составляющая

входного сигнала

x (t).

Предполагается, что выходной стационарный случайный сигнал может быть представлен в виде

y (t) = my + y (t),

(4.2)

где

my -математическое ожидание

y (t); y (t) -центрированная случайная состав-

ляющая

y (t).

Коэффициент

k 0= my / mx

(4.3)

называется статистическим коэффициентом усиления звена по математическо- му ожиданию.

Коэффициент

k 1= ± cr y / cr x

(4.4)

называется статистическим коэффициентом усиления нелинейного звена по

y

центрированной случайной составляющей, где cr 2

и cr 2-дисперсии

y (t) и

x (t).

x

С учетом того что нелинейные звенья в АСР работают совместно с ли- нейными, для которых законы преобразования случайных сигналов определя- ются не столько диспарсиями их, сколько корреляционными функциями, мож- но допустить при статистической линеаризации некоторую ошибку в дисперсии выходного сигнала с целью лучше приблизить его корреляционную функцию к

истинной. В этом случае

Дата добавления: 2015-08-20