|
Читайте также: |
Построение фазовых траекторий нелинейных АСР можно выполнить также методом изоклин с использованием уравнения (6.2). Для этого сначала на фазовой плоскости строят линии, соответствующие алгебраическому уравне- нию
H (y, z) = c = const
(7.1)
Каждому значению с (рисунок 6.3) соответствует своя линия, называемая изоклиной. Изоклина – это геометрическое место точке с одинаковым наклоном фазовых траекторий, проходящих через эти точки, т.е. для точек изоклины.
dz dy = c = const.
(7.2)
|
а устойчивый; б полуустойчивый; процесса по фазовой траектории:
в неустойчивый; г два предельных цикла
Используя свойство изоклин (7.2), фазовые траектории строят в следую-
щем порядке. Берут произвольную точку
M 1 на изоклине
с 1 и из нее проводят
две прямые до пересечения с изоклиной
с 2. Первую прямую проводят под уг-
лом arctg c 1, соответствующим углу наклона фазовых траекторий в точках изо-
клины
с 1. Вторую прямую проводят под углом arctg c 2, соответствующим углу
наклона фазовых траекторий в точках изоклины
c 2. Точка
M 2 на изоклине c 2
находится как середина пересечения изоклина
c 2 с обеими прямыми. Далее
аналогичным образом из точки
M 2 проводят две прямые с углами наклона
arctg c 2
и arctg c 3
до пересечения с изоклиной
c 3, на которой находят точку
M 3.
Поступая аналогичным образом, находят ряд точек лучают фазовую траекторию АСР.
M 1, соединив которые, по-
Отличительной особенностью фазовых портретов нелинейных АСР явля-
ется наличие в них замкнутых фазовых траекторий, называемых предельными циклами, которым соответствуют автоколебания. Предельные циклы бывают устойчивыми, полуустойчивыми и неустойчивыми.
Устойчивый предельным цикл соответствует устойчивым автоколебани- ям, он характеризуется тем, что фазовые траектории накручиваются на него с обеих сторон (рисунок 7.1, а). Полуустойчивый предельный цикл характеризу- ется тем, что фазовые траектории накручиваются на него с одной стороны и скручиваются с другой (рисунок 7.1, б). Для неустойчивого предельного цик- ла фазовые траектории скручиваются с него с обеих сторон (рисунок 7.1, в). Фазовый портрет нелинейных АСР может иметь несколько предельных циклов (рисунок 7.1, г).
Фазовый портрет нелинейных АСР, описываемых дифференциальным уравнениями не выше второго порядка, дает полное представление о динамике нелинейной системы при детерминированных воздействиях, включая точность, устойчивость и качество регулирования.
По фазовой траектории можно построить переходный процесс. Для этого поступают следующим образом (рисунок 7.2):
а) вычерчивают фазовую траекторию;
б)
число;
выбирают временной шаг Ë t
построения
y (t) = y (n Ë t), где n
целое
в) определяют угол
� = 2 arctg (Ë t / 2);
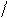г) из точки
y (t) = y 0, определяемой начальными условиями, проводят
прямую под углом
b 1:
= 900 �
2 до пересечения с фазовой траекторией в точке
д) из точки b 1
проводят прямую под углом � до пересечения с осью y в
точке
a 1;
e)
точку a 1
проецируют в плоскости
y (t) в точку
ж) из точки
a 1проводят прямую под углом = 90 �
2 до пересечения
с фазовой траекторией в точке
b 2;
точке
з) из точки b 2 a 2;
проводят прямую под углом � до перенесения с осью y в
и) точку a 2
проецируют в плоскости
y (t)
в точку
d 2;
поступая аналогич-
ным образом, находят точки
d 1искомой
y (t).
По построенному таким образом переходному процессу
y (t)
можно дос-
таточно объективно оценить качество регулирования в нелинейной АСР при различных начальных условиях.
Основная литература: 1 [134-145].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
1. Фазовые траектории систем с нелинейными элементами.
2. Метод получения переходного процесса по фазовой траектории.
Конспект лекции № 8
Тема лекции: 8 Устойчивость нелинейных систем. Методы Ляпунова
Предварительно заметим, что при изложении прямого метода Ляпунова, именуемого также же вторым методом Ляпунова, будем пользоваться диффе- ренциальными уравнениями автоматической системы в форме уравнений пер- вого порядка, или уравнении состояния, полагая, что они записаны для пере- ходного процесса в отклонениях всех переменных от их значений в установив-
шемся процессе при новых постоянных значениях возмущающего
f = f 0 и за-
дающего
g = g 0 воздействий. Следовательно, эти уравнения для нелинейной
системы n- го порядка будут:
dx 1= X (x, x,..., x),
dt 1 1 2 n
dx 2
= X 2 (x 1, x 2,..., xn),
(8.1)
dt
……………………
dxndt
= X n (x 1, x 2,..., xn),
где функции
X 1, X 2,..., X n
произвольны и содержат любого вида нелинейности,
но всегда удовлетворяют условию
X 1= X 2 =... = X n = 0 при
x 1= x 2=... xn = 0,
(8.2)
так как в установившимся состоянии все отклонения переменных и их произ- вольные равны, очевидно нулю по самому определению понятия этих отклоне- ний. Нам понадобятся в дальнейшем еще следующие сведения.
Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях. Пусть имеется функция нескольких переменных V = V (x 1, x 2,..., xn).
Представим себе трехмерное фазовое пространство, в котором
x 1, x 2,..., xn
явля-
ются прямоугловыми координатами (это будут, в частности, фазовая плоскость при n=2 и обычное трехмерное пространство при n=3). Тогда в каждой точке
указанного пространства функция V будет иметь некоторые определенные зна- чения. Нам панодобятся в дальнейшем функции V (x 1, x 2,..., xn), которые обра-
щаются в нуль в начале координат (т.е. при некоторой области вокруг него.
x 1= x 2=... xn = 0,) и непрерывны в
Функция V называется знакоопределенной некоторой области, если онга во
всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат.
Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция V называется знакопеременной, если она в данной области вокруг на- чала координат может иметь разные знаки.
Приведем примеры всех трех типов функции V. Пусть n=2 и
V = x 2+ x 2,
1 2
это будет знакоопределнная (положительная) функция, так как V
= 0 только то-
гда, когда одновременно
x = 0 и
x 2= 0, и V > 0
при всех вещественных значени-
2 2 2
ях x 1и
x 2. Аналогично при любом n функция
V = x 1
+ x 2+... + xn
будет знакооп-
ределенной положительной, а
V = (x 2+ x 2+... + x 2) - знакоопределенной отри-
цательной.
1 2 n
а) х3
0
х1
б) х3
х2
х 1= х 2
х2
0
в) х3
х1
А х2
0
х1
в
Рисунок 8.1 Примеры трех типов функции
Если взять функцию
V = x 2+ x 2
при n=3, то она уже не будет знакоопре-
1 2
делнной, так как, оставаясь положительной при любых
x 1, x 2 и
x 3она может об-
ращаться в нуль не только при
x 1= x 2= x 3= 0,
но также и при любом значении
x 3, если
x 1= x 2= 0 (т.е. на все оси
x 3, рисунок 8.1,а). Следовательно, это будет
знакопостоянная (положительная) функция.
Наконец, функция
V = x 2+ x 2
будет знакопеременной, так как она положитель-
1 2
на для всех точек плоскости справа от прямой тельна слева от этой прямой.
x 1= x 2
(рисунок 8.1, б) и отрица-
Заметим, что в некоторых частных задачах нам понадобится также же
функция V, которая обращается в нуль не в начале координат, а на заданном конечном отрезке АВ (рисунок 8.1, в). Тогда знакоопределенность функции V будет обозначать ее неизменный знак и необращение в нуль в некоторой об- ласти вокруг этого отрезка.
Функция Ляпунова и ее производная по времени. Любую функцию
V = V (x 1, x 2,... xn),
(8.3)
тождественно обращающуюся в нуль при
x 1= x 2=... xn = 0, будем называть
функцией Ляпунова, если в ней в качестве величин ния переменных в переходном процессе
x 1, x 2,..., xn
взяты те отклоне-
x 1= x 1(t),
x 2= x 2(t),..., xn = xn (t),
в которых записываются уравнения (8.1) для этой системы. Производная от функции Ляпунова (8.3) по времени будет
dV = ä V
dx 1+ ä V
dx 2 +... + ä V
dxn.
dt ä x 1 dt
ä x 2 dt
ä xn dt
Подставив сюда значения
dx 1,..., dxn
из заданных уравнений система в общем
dt dt
случае (8.1), получим производную от функции Ляпунова по времени в виде
dV = ä V dt ä x 1
X + ä V
X +... + ä V
|
X n,
где
X 1, X 2,..., X n - правые части уравнений (8.1), представляющие собой задан-
ные функции от отклонений
x 1, x 2,..., xn.
Следовательно, производная от функции Ляпунова по времени, так же, как и сама V, является некоторой функцией отклонений, т.е.
dV
= W (x 1, x 2,..., xn),
dt
(8.4)
причем согласно свойству (8.2) эта функция W, так же как и сама V, тождест-
венно обращается в нуль при
x 1= x 2=... = xn = 0. Поэтому к ней в одинаковой
степени можно применять все те же понятия знакоопределенности, знакопосто- янства и зна-копеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
Здесь шла речь только об уравнениях (нелинейных), в которые не входит в явном виде время t, так как только этот случай будет рассматриваться в даль- нейшем. Вообще же метод Ляпунова может применяться и при наличии време- ни t в явном виде, в частности для уравнений с переменными коэффициентами (линейных и нелинейных).
Базируясь на этих предварительных сведениях, дадим общую формули- ровку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоремы эти годятся для исследования устойчи-
вости систем регулирования не только при малых, но и при больших отклоне- ниях, если для них справедливы исходные уравнения данной системы регули- рования. Устойчивость системы при любых больших начальных отклонениях называется коротко устойчивостью в целом.
Теорема Ляпунова об устойчивости нелинейных систем. Теорема формулируется следующим образом: если при заданных в-форме (8.1) уравне- ниях системы п-го порядка можно подобрать такую знакоопределенную
функцию Ляпунова
V (x 1, x 2,..., xn), чтобы ее производная по времени
W (x 1, x 2,..., xn)
тоже была знакоопределенной (или знакопостоянной), но имела
знак, противоположный знаку V, то данная система устойчива. При знакооп- ределенной функции W будет иметь место асимптотическая устойчивость.
Проиллюстрируем справедливость этой теоремы на наглядных гео- метрических образах. Для простоты возьмем систему третьего порядка (п = 3). Уравнения (8.1) для нее в общем виде будут
dx 1 dt
= X (x, x, x), l
|
dx 2
dt dx 3
= X 2
(x 1, x 2
, x 3
),1
(8.5)
= X 3 (x 1, x 2, x 3). 1
dt J
виде
Возьмем знакоопределенную положительную функцию Ляпунова в
V = a 2 x 2 + b 2 x 2 + c 2 x 2
(8.6)
1 2 3
где а, b, с - произвольно заданные вещественные числа. Будем придавать ве-
личине V возрастающие постоянные значения: V = 0,
чает
C 1, C 2, C 3,....,
что озна-
a 2 x 2+ b 2 x 2+ c 2 x 2= 0
|
......................................·
Первое из этих выражений соответствует одной точке
x 1 = x 2 = x 3 = 0
(началу координат фазового пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсо- ид содержит внутри себя целиком предыдущий (рисунок 8.2).
Возьмем теперь производную от функции Ляпунова по времени. Со- гласно (8.3) и (8.4)
dV = 2 a 2
dt
x 1 X 1
(x 1, x 2
, x 3
)+ 2 b 2 x
X 2 (x 1, x 2
, x 3
) + 2 c 2
x 3 X 3 (x 1, x 2, x 3) = W (x 1, x 2, x 3),
где функции ния (8.5).
X 1, X 2, X 3
берутся из заданных уравнений системы регулирова-
Если полученная таким путем функция W(x1, x2, xs) окажется знакоопре-
деленной отрицательной, т. е. если
dV
dt -< 0
(8.7)
во всех точках исследуемого фазового пространства, кроме одного только
начала координат, где
dV = 0
dt
(при
x 1 = x 2
= x 3
= 0),
то при любых начальных условиях изображающая точка М (рис.17.10) вследствие (8.7)
Рисунок 8.2. Фазовое пространство
будет двигаться в сторону уменьшения значения F, т. е. будет пересекать эл- липсоиды, изображенные на рисунок 8.2, извне внутрь. В результате с течени- ем времени изображающая точка М будет стремиться к началу координат О фа- зового пространства и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла.
Это и означает затухание всех отклонений
x 1, x 2, x 3
в переходном процессе с
течением времени. Таким образом, установлена устойчивость данной системы регулирования, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакоопределенной функции W).
Отсюда вытекает справедливость теоремы и в общем случае. Рассужде- ния остаются аналогичными, только вместо трех уравнений (8.5) будет п урав- нений (8.1). Как и раньше, для любой знакоопределенной положительной
функции Ляпунова
V (x 1, x 2,..., xn) = C
получим некоторые замкнутые поверхно-
сти, окружающие начало координат (рисунок 8.1), но уже не в обычном трех- мерном, а в трехмерном фазовом пространстве (их иногда называют ги-
dV
перповерхностями). Поэтому, если производная
= W (x 1, x 2,..., xn) окажется
dt
мерном пространстве при любых начальных условиях с течением времени будет
пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.
Основная литература: 3 [324-348].
Дополнительная литература: 1 [365-414].
Контрольные вопросы:
Устойчивость и некоторые оценки качества нелинейных систем. Функция Ляпунова и ее производная по времени.
Теорема Ляпунова об устойчивости нелинейных систем. Когда функция V называется знакоопределенной?
Когда функция V называется знакопеременной? Когда функция V называется знакопостоянной?
Конспект лекции № 9
Тема лекции: 9 Условия абсолютная устойчивость нелинейных систем. Критерий Попова В.М.
Будем рассматривать нелинейные системы, структурную схему кото- рых можно привести к виду, показанному на рисунок 9.1. В этой схеме
имеется безынерционный нелинейный элемент с характеристикой
y = Ô(x)
и линейная часть с передаточной функцией W (s), имеющей статический ко- эффициент передачи, равный единице, и импульсной переходной функци-
ей kИ (t). Все воздействия приведены к одному входу и обозначены
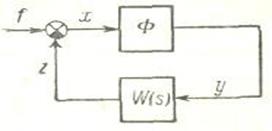
Рисунок 9.1. Структура нелинейных систем
f (t).
Изображение решения дифференциального уравнения системы выра-
зим через изображения воздействия F (s) и координаты
Y (s) = L {Ô x (t)]}:
X (s) = F (s) W (s) L {Ô x (t)]}
(9.1)
Переходя к оригиналам, получаем интегральное уравнение Вольтерра вто- рого рода:
x (t) =
f (t) z (t) =
f (t)
t
f k И
(t ¢Ñ)Ô x (¢Ñ)] d¢Ñ. (9.2)
Будем рассматривать систему при таких воздействиях, которые ограничены по модулю и являются исчезающими функциями времени. Обозначим максималь-
ное воздействие
sup
f (t)
(supremum).
Исчезающей функцией времени течением времени к нулю:
f (t)
назовем функцию, стремящуюся с
lim f (t) = 0.
t í00
Если воздействие отсутствует, то из (9.1) следует
t
x (t) = f k И
(t ¢Ñ)Ô x (¢Ñ)] d¢Ñ. (9.3)
Если нелинейная характеристика проходит через начало координат, т. е. Ф(0)=0, то уравнение (9.3) имеет тривиальное решение
x (t) = 0,
(9.4)
которое соответствует положению равновесия.
Положение равновесия устойчиво в смысле Ляпунова, если существует
такое положительное число
Ë (A) > 0, что при
имеет место неравенство
sup
f (t) = Ë (A)
(9.5)
x (t):: A,
(9.6)
где А — сколь угодно малое положительное число.
В зависимости от того, при каких значениях
Ë (A)
выполняются нера-
венства (9.5) и (9.6), будем различать три вида устойчивости: у с т о й ч и -
в о с т ь в м а л о м, если
Ë (A)
бесконечно малая; у с т о й ч и в о с т ь в
большом, если
sup
f (t)
- конечная величина, и у с т о й ч и в о с т ь в ц е лом,
если
sup
f (t)
не ограничено.
Абсолютной устойчивостью называют устойчивость положения равнове- сия в целом, имеющую место для характеристик Ф (х), принадлежащих к како- му-либо определенному классу.
Наиболее разработанными являются методы исследования абсолютной устойчивости для класса характеристик Ф (х), заключенных между двумя пря- молинейными лучами, проходящими через начало координат в первом и треть- ем квадрантах и имеющими угловые коэффициенты r и К.
Характеристики, удовлетворяющие этому ограничению, будем называть характеристиками, принадлежащими сектору (r, К).
Частотный метод В. М. Попова
Решение задачи об абсолютной устойчивости системы с одной однознач- ной нелинейностью (т. е. устойчивости при любой форме этой нелинейности со слабым ограничением типа с помощью теорем прямого метода Ляпунова было проиллюстрировано на двух примерах. Изложим теперь частотный метод, предложенный румынским ученым В. М. Поповым, при использовании ко- торого та же задача решается более простыми приемами, аналогичными час- тотным способам исследования устойчивости линейных систем.
Дата добавления: 2015-08-20; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Конспект лекции №1 2 страница | | | Конспект лекции №1 4 страница |
