Читайте также:
|
Как следует из выражения
,
при проведении экспоненциального сглаживания необходимо знать начальное (предыдущее) значение сглаживаемой функции. В некоторых случаях за начальное значение можно взять первое наблюдение, чаще начальные условия определяются согласно выражениям (5.4) и (5.5). При этом величины 
, 
и 
определяются методом наименьших квадратов.
Если мы не очень доверяем выбранному начальному значению, то, взяв большое значение постоянной сглаживания 
через k наблюдений, мы доведем «вес» начального значения до величины 
, и оно будет практически забыто. Наоборот, если мы уверены в правильности выбранного начального значения и неизменности модели в течение определенного отрезка времени в будущем, может быть выбрано малым (близким к 0).
Таким образом, выбор постоянной сглаживания (или числа наблюдений в движущейся средней) предполагает принятие компромиссного решения. Обычно, как показывает практика, величина постоянной сглаживания лежит в пределах от 0,01 до 0,3.
Известно несколько переходов, позволяющих найти приближенную оценку . Первый вытекает из условия равенства скользящей и экспоненциальной средней
,
где m – число наблюдений в интервале сглаживания. Остальные подходы связываются с точностью прогноза.
Так, возможно определение исходя из соотношения Мейера:
,
где 
– среднеквадратическая ошибка модели;
– среднеквадратическая ошибка исходного ряда.
Однако использование последнего соотношения затруднено тем, что достоверно определить и из исходной информации весьма сложно.
Часто параметр сглаживания, а заодно и коэффициенты и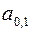 
подбирают оптимальными в зависимости от критерия
путем решения алгебраической системы уравнений, которую получают, приравнивая к нулю производные
; 
; 
.
Так, для линейной модели прогнозирования исходный критерий равен
.
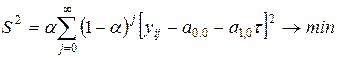Решение этой системы с помощью ЭВМ не представляет никаких сложностей.
Для обоснованного выбора также можно использовать процедуру обобщенного сглаживания, которая позволяет получить следующие соотношения, связывающие дисперсию прогноза и параметр сглаживания для линейной модели:
для квадратичной модели
,
где 
; – СКО аппроксимации исходного динамического ряда.
Вопросы для самопроверки по разделу 5
1. В чем суть метода экстраполяции сглаживания?
2. Что такое интервал сглаживания?
3. Как происходит расчет скользящей средней при большом числе уровней?
4. Как выглядит общая запись в рекуррентной форме экспоненциальной средней порядка 
?
5. Как определяются параметры прогнозной модели методом экспоненциального сглаживания?
6. Какова последовательность вычисления прогнозных значений?
7. Как выбирается начальное значение сглаживаемой функции?
8. Что такое матрица прецедентов?
Дата добавления: 2015-07-25; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение параметров прогнозной модели методом экспоненциального сглаживания | | | Обоснование периода упреждения |