Сущность метода экспоненциального сглаживания

Сущность метода состоит в том, что динамический ряд сглаживается с помощью взвешенной «скользящей средней», в которой веса подчиняются экспоненциальному закону. Другими словами, чем дальше от конца временного ряда отстоит точка, для которой вычисляется взвешенная скользящая средняя, тем меньше «участия она принимает» в разработке прогноза.

Пусть исходный динамический ряд состоит из уровней (составляющих ряда) 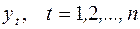. Для каждых последовательных уровней этого ряда (m<n) можно подсчитать среднюю величину. Вычислив значение средней для первых уровней , переходят затем к расчету средней для уровней и так далее. Таким образом, интервал сглаживания, то есть интервал, для которого подсчитывается средняя, как бы скользит по динамическому ряду с шагом, равным единице. Если – нечетное число, а предпочтительно брать нечетное число уровней, поскольку в этом случае расчетное значение уровня окажется в центре интервала сглаживания и им легко заменить фактическое значение, то для определения скользящей средней можно записать следующую формулу:

,

где – значение скользящей средней для момента ();

– фактическое значение уровня в момент ;

– порядковый номер уровня в интервале сглаживания.

Величина определяется из продолжительности интервала сглаживания.

Поскольку

при нечетном , то

.

Расчет скользящей средней при большом числе уровней можно упростить, определяя последовательные значения скользящей средней рекурсивно:

.

Но исходя из того, что последним наблюдениям необходимо придать больший «вес», скользящее среднее нуждается в ином толковании. Оно заключается в том, что полученная с помощью усреднения величина заменяет не центральный член интервала усреднения, а его последний член. Соответственно этому последнее выражение можно переписать в виде

. (5.1)

Здесь скользящая средняя, относимая к концу интервала, обозначена новым символом . По существу, равно , сдвинутому на шагов вправо, то есть , где .

Учитывая, что является оценкой величины , выражение (5.1) можно переписать в виде

, (5.2)

где является оценкой , определяемой выражением (5.1).

Если вычисления (5.2) повторять по мере поступления новой информации и переписать в ином виде, то получим сглаженную функцию наблюдений:

,

или в эквивалентной форме

(5.3)

Вычисления, проводимые по выражению (5.3) с каждым новым наблюдением, называются экспоненциальным сглаживанием. В последнем выражении для отличия экспоненциального сглаживания от скользящего среднего введено обозначение вместо 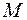. Величина , являющаяся аналогом , называется постоянной сглаживания. Значения лежат в интервале . Если представить в виде ряда

,

то нетрудно заметить, что «веса» убывают по экспоненциальному закону во времени. Например, для получим

0,2 + 0,16 + 0,128 + 0,102 + 0,082 + …

Сумма ряда стремится к единице, а члены суммы убывают со временем.

Величина в выражении (5.3) представляет собой экспоненциальную среднюю первого порядка, то есть среднюю, полученную непосредственно при сглаживании данных наблюдения (первичное сглаживание). Иногда при разработке статистических моделей полезно прибегнуть к расчету экспоненциальных средних более высоких порядков, то есть средних, получаемых путем многократного экспоненциального сглаживания.

Общая запись в рекуррентной форме экспоненциальной средней порядка имеет вид

.

Величина изменяется в пределах 1, 2, …, p, p+1, где p – порядок прогнозного полинома (линейного, квадратичного и так далее).

На основе этой формулы для экспоненциальной средней первого, второго и третьего порядков получены выражения

;

;

.

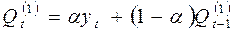Дата добавления: 2015-07-25