Измерение колеблемости в рядах динамики

Как уже отмечалось, уровни ряда динамики формируются под влиянием различных взаимодействующих факторов, одни из которых определяют тенденцию развития, а другие – колеблемость (вариацию).

Изучение колеблемости в рядах динамики как предмета исследования часто является самостоятельной задачей математической статистики.

Колебания уровней ряда могут носить разный характер. Исследователи временных рядов всегда пытались классифицировать факторы, вызывающие те или иные колебания, и соответственно выделить типы колебаний. Большинство авторов чаще всего выделяют (наряду с трендом) циклические (долгопериодические), сезонные (обнаруживаемые в рядах, где данные приведены за кварталы или месяцы) и случайные колебания.

Для измерения колеблемости уровней в рядах динамики могут использоваться показатели, аналогичные показателям вариации признака:

- размах, или амплитуда, отклонений отдельных уровней от их средней (по модулю) или от тренда;

- среднее линейное отклонение d (по модулю) отдельных уровней от общей средней или от тренда;

- среднее квадратическое отклонение а отдельных уровней от общей средней или от тренда;

- относительный показатель колеблемости уровней, аналогичный коэффициенту вариации, .

При этом важно учитывать, относительно какого показателя (уровня) исследуется колеблемость. Например, можно исследовать колеблемость вокруг среднего уровни ряда у, который на графике выразится прямой, параллельной оси абсцисс. А можно исследовать колебания уровней вокруг линии тренда (или скользящей средней). Различный характер таких колебаний наглядно виден на графике (рис. 3.1).

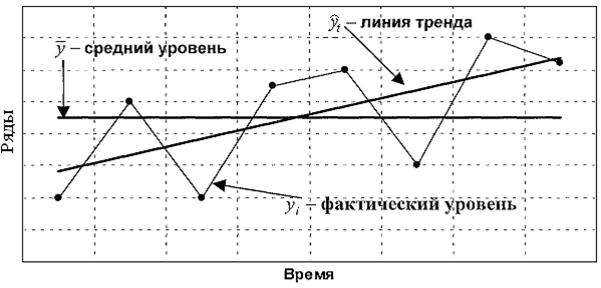
Рис. 3.1. Колебания фактических уровней y_i относительно среднего уровня и линии тренда

Рассмотрим традиционный случай расчета среднего квадратического отклонения отдельных уровней y_t от общего среднего уровня ряда :

. (3.3)

В данном случае величина характеризует сумму квадратов отклонений фактических уровней от общей средней, за счет всех факторов, формирующих уровни, как основных, определяющих тренд, так и случайных.

Задача исследования колебаний уровней в рядах динамики сводится к разложению общей колеблемости на составляющие и выделению именно тех колебаний, которые интересуют исследователя.

Для решения этой задачи требуется разложить общую сумму квадратов отклонений от средней на составляющие.

Имея фактические (эмпирические) уровни ряда у и уровни, выровненные по определенному тренду, y_t можно рассчитать следующие суммы квадратов отклонений:

1) 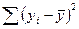– общую сумму квадратов отклонений фактических уровней от их общей средней;

2) 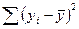– сумму квадратов отклонений за счет тренда (за счет фактора времени);

3) 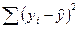– сумму квадратов отклонений за счет случайных факторов.

Согласно правилу сложения вариации и правилу сложения дисперсий первая сумма равна сумме двух последних:

Отсюда, пользуясь величиной 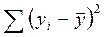, можно рассчитать среднее квадратическое отклонение уровней ряда за счет тренда (фактора времени).

В свою очередь, используя 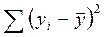, можно рассчитать среднее квадратическое отклонение уровней за счет случайных факторов. Чем меньше эта сумма, тем ближе фактические уровни к линии тренда. Это означает, что линия тренда подобрана удачно, то есть адекватна эмпирическим данным. Поэтому среднее квадратическое отклонение, рассчитанное на основе данной суммы квадратов отклонений от тренда, одновременно рассматривается как средняя квадратическая ошибка уравнения тренда. При этом поскольку разные уравнения тренда имеют различное число параметров т,средняя квадратическая ошибка уравнения тренда S (или 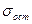) рассчитывается путем деления 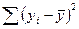не на п,а на (п – т), то есть на число степеней свободы:

(3.4)

Если уровни ряда являются месячными или квартальными показателями и несут на себе влияние сезонности, то в общей сумме квадратов отклонений уровней ряда от их средней 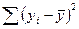можно выделить также составляющую, характеризующую сезонные колебания.

Дата добавления: 2015-07-25