Расчет индексов сезонности за ряд лет

При наличии месячных данных за ряд лет расчет индексов сезонности можно осуществить по-разному. Рассмотрим несколько способов.

1. По данным ряда лет рассчитывается среднее значение уровня для каждого месяца 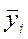, а также средний месячный уровень за весь период 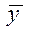. Затем определяются индексы сезонности как процентное отношение средних уровней для каждого месяца к общему среднему месячному уровню всего ряда (за все годы), то есть по

формуле

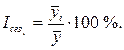(3.7)

Например, по данным табл. 3.3 за 2 года получим следующие средние уровни по месяцам:

в январе 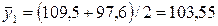кг;

в феврале 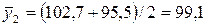кг;

в марте 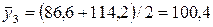кг.

Средний месячный уровень за 2 года

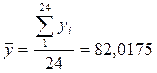тыс. т. 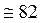кг.

Отсюда индексы сезонности :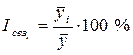

в январе ;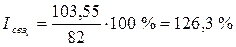

в феврале ;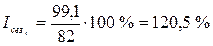

в марте .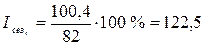

Данный метод используется в основном в тех случаях, когда уровни одноименных месяцев в разные годы отличаются незначительно.

Если же наблюдается тенденция к увеличению или снижению уровней из года в год, то эффективнее рассчитывать индексы сезонности по следующей схеме.

2. Для каждого года отдельно рассчитываются индексы сезонности по формуле 3.5, то естькак 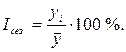, а затем из индексов одноименных месяцев находится средняя арифметическая.

Покажем этот метод на примере данных табл. 3.3. Рассчитаем индексы сезонности для 2007г. так же, как для 2006г.

В 2001 г. средний месячный уровень 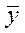составил 87,3 тыс.т. Отсюда месячные индексы сезонности 2001 г:

в январе ;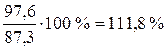

в феврале ;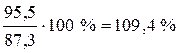

в марте 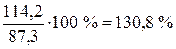и т.д.

Зная месячные индексы сезонности за 2006 г. (табл. 3.5) и за 2007 г., определяем из них для каждого месяца среднюю арифметическую, которую и принимаем в качестве обобщенной меры сезонных колебаний:

в январе ;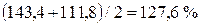

в феврале ;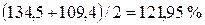

в марте 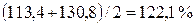и т. д.

3. Следующий прием измерения сезонных колебаний при наличии тренда в данных за ряд лет основан на сопоставлении фактических месячных (или квартальных) уровней либо со сглаженным методом скользящей средней, либо с выровненными определенной аналитической формуле.

В первом случае месячные данные за ряд лет сглаживаются 12-месячной скользящей средней (при квартальных данных – 4-квартальной скользящей средней). Затем фактические уровни каждого месяца (или квартала) выражают в процентах к скользящей средней.

На основе таких отношений (индексом сезонности) за ряд лет находится средняя арифметическая для каждого месяца (или квартала). Полученные усредненные индексы сезонности и являются искомыми, характеризующими «сезонную волну».

Аналогично рассчитываются индексы сезонности и во втором случае на основе сопоставления фактических уровней с выровненными по аналитической формуле. Здесь та же последовательность расчетов с той лишь разницей, что вместо сглаженных скользящих средних сначала находится уравнение тренда и по нему рассчитываются выровненные (теоретические) уровни 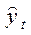. Затем определяется отношение фактических уровней к выровненным, то есть

рассчитываются индексы сезонности для каждого месяца (или квартала):

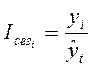. (3.8)

Поскольку за п лет отдельные месяцы повторяются, значения месячных индексов сезонности для отдельных лет усредняются.

Рассмотрим этот метод расчета индексов сезонности по отношению к тренду на условном примере динамики объема строительных работ в одном из районов города по кварталам за 3 года. Исходные данные и последующие расчеты показаны и табл. 3.6.

Предполагая, что фактические уровни у (графа 2 табл. 3.6) имеют линейный тренд, иведя счет времени от начала ряда (t=1,2, 3,...), подсчитываем все необходимые суммы в таблице (графы 2–5). По этим суммам и определяем параметры а₀ и f_lj, решая систему нормальных уравнений:

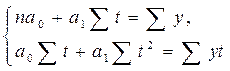, то есть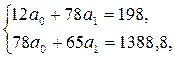

или сразу по формулам

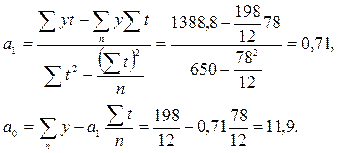
Отсюда уравнение тренда

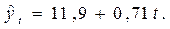
Подставляя в него значения t=1,2,...,12, находим выровненные уровни 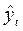, (с точностью до одной десятой) (графа 6 табл. 3.6).

Отношения фактических уровней 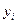(графа 2) к выровненным (теоретическим) 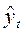(графа 6) и являются индексами сезонности (графа 7) по отношению к тренду.

Поскольку квартальные индексы в разные годы различны, они усредняются. Например, для I квартала 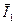=(89,7 + 89,6 + 85,8)73 = 88,4, для II квартала 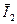=(91,7 + 96,3 + 97,4)73–95,1 и т. д.

Усредненные значения записываются в качестве искомых индексов сезонности для всех трех лет (графа 8).

Умножая выровненные уровни на средние индексы сезонности, получаем теоретические (выровненные) уровни с учетом «сезонной волны» (графа 9).

Таблица 3.6. Расчет величин для определения индексов сезонности по отношению к тренду

Год	Квар-тал	Выпол-нено работ, млн. руб.	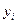Вре-мя t	t2	yt	Выровненные уровни	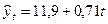Индекс сезонности, %	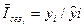Сред- ний индекс сезон-ности	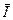Выров–ненные уровни с учетом сезон–ности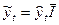
А
	I II III IV	11,3 12,2 17,5 14,4			11,3 24,4 52,5 57,6	12,6 13,3 14,0 14,7	89,7 91,7 125,0 98,0	88,4 95,1 121,3 95,1	11,1 12,6 17,0 13,9
	I II III IV	13,8 15,6 20,2 17,4			69,0 93,6 141,4 139,2	15,4 16,2 16,9 17,6	89,6 96,3 119,5 99,0	88,4 95,1 121,3 95,1	13,6 1,4 20,5 16,7
	I II III IV	15,7 18,4 23,5 18,0			141,3 184,0 258,5 216,0	18,3 18,9 19,7 20,4	85,8 97,4 119,3 88,2	88,4 95,1 121,3 95,1	16,1 17,9 23,9 19,4
		198,0			1388,8	198,0	1199,5 (1200)	1199,7 (1200)	198,1

Дата добавления: 2015-07-25