Прогнозирование с учетом индекса сезонности

Индексы сезонности используются при прогнозировании. Так, зная уравнение тренда и средние индексы сезонности, можно продлить наш ряд, то есть спрогнозировать квартальные уровни, например, в 2008 при условии, что выявленная для 2005-2007 гг. закономерность развития устойчива и сохранится в прогнозируемом периоде. Этот метод продления в будущее закономерности (тенденции), выявленной в прошлом, называется экстраполяцией.

В общем виде

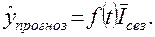
В нашем примере

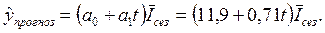
Подставляя соответствующие значения t и индексов сезонности, получаем следующий прогноз на 2008 г.:

I квартал 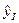= (11,9+0,71*13)*0,884=18,7 млн. руб.;

II квартал 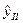= (11,9+0,71*14)*0,951=20,8 млн. руб.;

III квартал 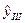= (11,9+0,71*15)*1,213=27,4 млн. руб.;

IV квартал 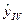= (11,9+0,71*16)*0,951=22,1 млн. руб.

Рассмотренная схема учета «сезонной волны» (умножение тренда на индекс сезонности) является мультипликативной.

Возможна и другая схема учета сезонной волны – аддитивная, когда к тренду прибавляется средняя величина абсолютных отклонений.

Чтобы экстраполировать ряд, приведенный в табл. 3.6, по аддитивной схеме, определим отклонение фактических уровней от выровненных и выполним все необходимые расчеты в табл. 3.7.

По аддитивной схеме 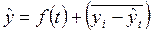= тренд + средние отклонения по кварталам.

В нашем примере прогноз на 2008 г., выполненный по аддитивной схеме, даст следующие показатели по кварталам:

I квартал 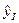= (11,9+0,71*13)-1,83=19,3 млн. руб.;

II квартал 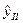= (11,9+0,71*14)-0,73=21,05 млн. руб.;

III квартал 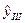= (11,9+0,71*15)+3,53=26,08 млн. руб.;

IV квартал 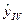= (11,9+0,71*16)-0,97=22,29 млн. руб.

Результаты прогнозирования, полученные по мультипликативной и аддитивной схемам, несколько отличаются, но эти различия не столь значительны. Вообще, точечный прогноз весьма сомнительное дело. Обычно для прогнозируемых показателей с заданной вероятностью определяются интервалы «от и до», которые учитывают среднюю квадратическую ошибку уравнения тренда.

Таблица 3.7. Экстраполяция ряда по аддитивной схеме

Год	Квартал	Фактические уровни	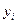Выровнен-ные уровни (тренд)	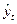Абсолютное отклонение от тренда	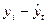Среднее отклонение по кварталам	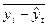Выровненные уровни с учетом сезонности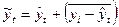
А
	I II III IV	11,3 12,2 17,5 14,4	12,6 13,3 14,0 14,7	-1,3 -1,1 3,5 -0,3	-1,83 -0,73 3,53 -0,97	10,77 12,57 17,53 13,73
	I II III IV	13,8 15,6 20,2 17,4	15,4 16,2 16,9 17,6	-1,6 -0,6 3,3 -0,2	-1,83 -0,73 3,53 -0,97	13,57 15,47 20,43 16,63
	I II III IV	15,7 18,4 23,5 18,0	18,3 18,9 19,7 20,4	-2,6 -0,5 3,8 -2,4	-1,83 -0,73 3,53 -0,97	16,47 18,17 23,23 19,43
		198,0	198,0			198,0

Дата добавления: 2015-07-25