Парные регрессии, сводящиеся к линейному тренду

Используя метод наименьших квадратов, можно построить практически любые формы нелинейной парной связи. Для этого используют линеаризующие преобразования, так как только линейные по параметрам функции восстанавливаются с помощью МНК.

Широко распространены два вида преобразований: натуральный логарифм ln и обратное преобразование I/t. При этом, очевидно, возможно преобразование как зависимой переменной y,так и независимой переменной t(x) или одновременно той и другой.

В табл. 2.1. приведены восемь часто встречающихся преобразований парных зависимостей, полученных комбинацией из индивидуальных преобразований зависимой переменной у и независимой переменной t. Качество прогнозирования проверяют на основе уравнения

.

После вычисления коэффициентов и по методу наименьших квадратов выполняют обратные преобразования, то есть по и определяют a и b.

Так, например, простая экспоненциальная кривая (экспонента) определяется уравнением

,

где e – основание натурального логарифма.

Это уравнение можно переписать в другом виде:

, где

или 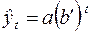, где .

Таблица 2.1. Функции и линейные преобразования

Функция	Линеаризующие преобразования	Вид кривой
Название	Уравнение	Преобра- зование переменных	Выражения для величин a и b
Линейная		y	t	a	b
Экспонен- циальная (простая)		ln y	t	ln a	b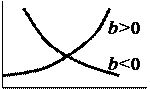
Степенная		ln y	ln t	ln a	b
Гиперболи- ческая 1 типа		y	t	a	b
Гиперболи- ческая 2 типа		y	t	a	b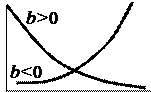
Гиперболи- ческая 3 типа		y	t	b	a
Логариф-мическая		y	ln t	a	b
Обратно-логариф-мическая		y	ln t	a	b
S-образная		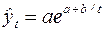ln y	t	a	b

От обеих частей исходного уравнения возьмем натуральный логарифм. Получим

или

.

Параметры и определим МНК и, преобразуя , снова перейдем к исходному уравнению.

Для конкретизации примера используем исходные данные, отражающие изменения количества типовых объектов (табл. 1.1), с учетом линеаризующих преобразований составим новую таблицу (табл. 2.2).

Таблица 2.2. Исходные данные для определения параметров экспоненциальной прогнозной модели

T, год
t
yt, шт.
	6,425	5,389	5,342	5,283	5,263	5,298	5,293
	5,425	10,778	16,027	21,133	26,313	31,790	37,053
T, год
t
yt, шт.
	5,283	5,252	5,176	5,165	5,118	5,263	4,970
	42,266	47,270	51,761	56,813	61,416	68,415	69,577

; ; ; .

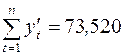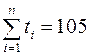В соответствии с системой уравнений (1.3) систему нормальных уравнений запишем в виде

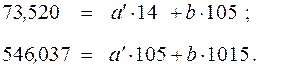
Решение этой системы дает

;

;

.

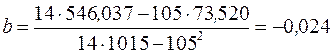Уравнение регрессии, следовательно, имеет вид

,

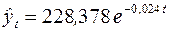а точечный прогноз на 2005 г. ()

объекта.

Для линеаризованных выражений также можно найти среднеквадратические ошибки оценок параметров и значений 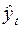. Отсюда можно определить и среднеквадратическую погрешность прогноза. Воспользуемся в чисто иллюстративных целях данными нашего примера, в котором мы оценили параметры экспоненты. Определим теперь доверительные интервалы для нее.

Поскольку уравнение содержит два оцениваемых параметра, то число степеней свободы при расчете квадратического отклонения составит 14–2=12; необходимые для расчета квадратического отклонения разности между фактическими и расчетными значениями логарифмов уровней приведены в табл. 2.3.

Сумма квадратов отклонений (в логарифмах) равна 0,047.

В соответствии с выражением (1.5)

и

.

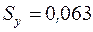Так как прогноз осуществлялся для (на 1995 г.), , то

(табл. 2.2)

.

Таблица 2.3. Расчет отклонений от экспоненциального тренда

t
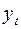
	5,425	5,389	5,342	5,283	5,263	5,298	5,293
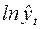
	5,404	5,380	5,356	5,332	5,308	5,284	2,260
	0,021	0,009	–0,014	–0,049	–0,045	0,014	0,033
t
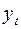
	5,283	5,252	5,176	5,165	5,118	5,263	4,970
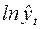
	5,236	5,212	5,188	5,164	5,140	5,116	5,092
	0,047	0,040	–0,012	0,001	–0,022	0,147	–0,122

Для данного примера t -статистика Стьюдента равна 1,78. Таким образом, .

Доверительный интервал определится следующим выражением:

,

что будет соответствовать 129-180 объектам.

Часто при прогнозировании тенденций развития техники необходимо определять предельные значения изучаемых переменных, изменяющихся по экспоненте. Такие величины имеют начальные значения и предел, к которому стремятся в бесконечности, (асимптоту).

Доказано, что финишные участки экспоненциальной кривой хорошо аппроксимируются гиперболической зависимостью

.

Разделив числитель и знаменатель правой части этого выражения на t, нетрудно заметить, что

, при .

Параметр b определяется методом наименьших квадратов после линеаризующей замены переменных согласно табл. 2.1.

Дата добавления: 2015-07-25