Выявление и измерение сезонных колебаний

В рядах динамики, уровни которых являются месячными или квартальными показателями, наряду со случайными колебаниями, часто наблюдаются сезонные колебания, под которыми понимается периодически повторяющееся из года в год повышение и снижение уровней в отдельные месяцы или кварталы.

Сезонным колебаниям подвержены внутригодовые уровни многих показателей. Так, например, расход электроэнергии в летние месяцы значительно меньше, нежели в зимние. Потребление мяса больше в зимние месяцы, производство некоторых видов продуктов (сахара, растительного масла и др.), связанных с переработкой сельскохозяйственной продукции, увеличивается в месяцы, непосредственно следующие за окончанием уборки урожая, рыночные цены на овощи в отдельные месяцы далеко не одинаковы и т. д.

При графическом изображении таких рядов сезонные колебания проявляются в повышении и снижении уровней в определенные месяцы (или кварталы).

В качестве иллюстрации рядов с сезонными колебаниями могут служить данные по продаже изделий за 2006-2007, по месяцам (табл. 3.3) и их графическое изображение (рис. 3.2).

Таблица 3.3. Данные по продаже изделий за 2006–2007 гг.

Год	Месяц
	109,5	102,7	86,6	82,3	76,6	70,0	57,6	24,5	36,3	70,7	95,2	104,5
	97,6	95,5	114,2	101,3	105,6	94,6	75,2	38,6	38,9	78,7	96,5	111,0

2006 2007

Рис. 3.2. Динамика продаж

Таблица 3.4. Квартальные данные по продажам

Год
Квартал	I	II	III	IV	I	II	III	IV
Продано, кг	298,8	228,9	118,4	270,4	307,3	301,5	152,7	286,2

Вместо месячных показателей могут быть квартальные. Если колебания не случайны, они сохраняются и в квартальных уровнях, как это показано в табл. 3.4, где месячные данные нашего примера преобразованы в квартальные, и на рис. 3.3.

Наблюдение за сезонными колебаниями позволяет, с одной стороны, устранить их там, где они нежелательны (например, можно более равномерно использовать в течение года строительных рабочих), с другой стороны, решить ряд практических задач (например, определить потребности в рабочей силе, оборудовании и сырье в тех отраслях, где влияние сезонности велико).

2006 2007

Рис. 3.3. Динамика продаж по кварталам

При изучении рядов динамики, содержащих «сезонную волну», ее выделяют из общей колеблемости уровней и измеряют. Существует ряд методов для решения этой задачи. Все они основаны на сравнении фактических уровней каждого месяца (или квартала) со средним уровнем, предполагающим равномерное распределение годового показателя по месяцам (или кварталам), либо со сглаженными скользящими средними или выровненными по уравнению тренда.

Таблица 3.5. Сезонные колебания продаж

Месяц	Продажа	Индекс сезонности, % к среднему месечному уровню	Абсолютное отклонение от среднего месячного уровня	Абсолютное отклонение, % к среднему месячному уровню
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь	109,5 102,7 86,6 82,3 76,6 70,0 57,6 24,5 36,3 70,7 92,2 104,5	143,4 134,5 113,4 107,8 100,3 91,6 75,4 32,1 47,5 92,6 124,6 136,8	33,125 26,325 10,225 5,925 0,225 -6,375 -18,375 -51,875 -40,075 -5,675 18,825 28,125	43,4 34,5 13,4 7,8 0,3 -8,4 -24,6 -67,9 -52,5 -7,4 24,6 36,8	1883,56 1190,25 179,56 60,84 0,09 70,56 605,16 4610,41 2756,25 54,76 605,16 1354,24	1097,266 693,006 104,551 35,106 0,051 40,641 352,501 2691,018 1606,006 32,206 354,381 791,016
Итого	916,5				13370,84	7797,747

При этом для измерения «сезонной волны» рассчитывают либо абсолютные разности (отклонения) фактических уровней от среднего уровня (или от выровненных), либо отношения месячных уровней к среднему месячному уровню за год, так называемые индексы сезонности:

(3.5)

В табл. 3.5 показан расчет индексов сезонности и абсолютных отклонений уровней от среднего на примере данных о продажах товара в 2006 г.

Средний месячный уровень за год кг.

В графе 3 табл. 3.5 индексы сезонности рассчитаны как процентное отношение фактического уровня каждого месяца 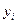к среднему месячному у за год, то есть по формуле (3.5). В графе 4 приведены абсолютные отклонения уровней каждого месяца от среднего месячного за год, а в графе 5 – эти же отклонения в процентах к среднему месячному уровню. Нетрудно видеть, что данные графы 5 представляют собой разность между индексом сезонности и 100 %. Другими словами, независимо от того, как учитываются различия в месячных уровнях, измерение сезонности в конечном счете сводится к расчету индексов сезонности.

Графическое изображение индексов сезонности (рис. 3.4) наглядно показывает форму, характер «сезонной волны» относительно среднего месячного уровня за год, принимаемого за 100 %.

Рис. 3.4. Индексы сезонности продажи в 2006 году

Данные табл. 3.5 и рис. 3.4 показывают, что минимальный объем продаж приходился на август, а максимальный – на январь.

Для характеристики силы (меры) колеблемости уровней динамического ряда из-за сезонной неравномерности часто предлагается использовать среднее квадратическое отклонение индексов сезонности (в процентах) от 100 %, то есть

(3.6)

В нашем примере сумма рассчитана в графе 6 (см. табл. 3.5).

Тогда

Этот же результат можно получить и по-другому, как коэффициент вариации (колеблемости):

где – квадратическое отклонение уровней ряда.

В табл. 3.5 сумма квадратов отклонений от среднего уровня рассчитана в графе 7, среднее значение уровня . Отсюда

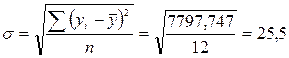кг,

то есть результаты двух показателей (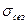 и V)идентичны.

Необходимо отметить, что в формуле (3.3) сумма квадратов отклонений месячных уровней от общего среднего уровня, то есть , измеряет колеблемость за счет всех факторов, а не только за счет сезонной неравномерности, поэтому, пользуясь ею для измерения колеблемости ряда из-за сезонной неравномерности, не следует переоценивать ее значение.

Конечно, там, где колебания в основном определены влиянием сезонности, расчет по формуле (3.3) их учитывает. Однако при этом не исключается и влияние случайных колебаний.

В рассмотренном методе расчета индексов сезонности 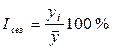использовались данные одного года. Этот метод довольно прост, но, в силу элемента случайности, месячные данные одного года недостаточно надежны для определения меры се­зонных колебаний. Поэтому рекомендуется пользоваться месячными (или квартальными) данными за ряд лет (в основном за 3 года, хотя не исключена возможность использования данных за 2 года, а также за период более 3 лет).

Дата добавления: 2015-07-25