Определение параметров прогнозной модели методом экспоненциального сглаживания

Очевидно, что для разработки прогнозных значений на основе динамического ряда методом экспоненциального сглаживания необходимо вычислить коэффициенты уравнения тренда через экспоненциальные средние. Оценки коэффициентов определяются по фундаментальной теореме Брауна-Мейера, связывающей коэффициенты прогнозирующего полинома с экспоненциальными средними соответствующих порядков:

,

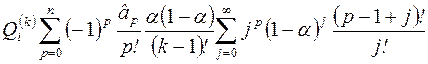где – оценки коэффициентов полинома степени р.

Коэффициенты находятся решением системы () уравнений с неизвестными.

Так, для линейной модели

;

;

для квадратичной модели

;

;

.

Прогноз реализуется по выбранному многочлену соответственно для линейной модели

;

для квадратичной модели

,

где – шаг прогнозирования.

Необходимо отметить, что экспоненциальные средние можно вычислить только при известном (выбранном) параметре, зная начальные условия .

Оценки начальных условий, в частности, для линейной модели

(5.4)

для квадратичной модели

(5.5)

где коэффициенты 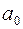и вычисляются методом наименьших квадратов.

	Расчет коэффициентов ряда методом наименьших квадратов
	Определение интервала сглаживания
	Вычисление постоянной сглаживания
	Вычисление начальных условий
	Вычисление экспоненциальных средних
	Вычисление оценок a0, a1 и т.д.
	Расчет прогнозных значений ряда

Рис. 5.1. Последовательность вычисления прогнозных значений

Величина параметра сглаживания приближенно вычисляется по формуле

,

где – число наблюдений (значений) в интервале сглаживания.

Последовательность вычисления прогнозных значений представлена на рис. 5.1.

В качестве примера рассмотрим процедуру получения прогнозного значения безотказной работы изделия, выражаемой наработкой на отказ.

Исходные данные сведены в табл. 5.1.

Выбираем линейную модель прогнозирования в виде

Решение осуществим со следующими значениями начальных величин: ; ; .

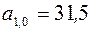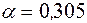Таблица 5.1. Исходные данные

Т, год
Номер наблюдения, t
Длина шага, прогнозирования,
Наработка на отказ, y (час)
j

При этих значениях вычисленные «сглаженные» коэффициенты для величины 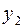будут равны

;

,

при начальных условиях

;

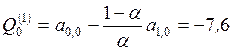и экспоненциальных средних

;

.

«Сглаженная» величина 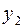при этом вычисляется по формуле

.

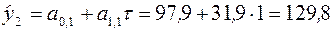Результаты дальнейших вычислений сведены в табл. 5.2.

Таблица 5.2. Результаты вычислений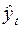

Величина	Номер наблюдения, t при
	–7,6	25,2	54,1	83,4	1,0	151,3
	–79,4	–47,5	–16,5	14,0	46,0	78,1
	64,2	97,9	124,7	154,8		224,5
	31,4	31,9	30,9	30,4
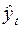
	95,7	129,8	155,6	185,6	224,5	256,5

Таким образом (табл. 5.2), линейная прогнозная модель имеет вид

.

Вычислим прогнозные значения для периодов упреждения в 2 года (), 4 года () и так далее наработки на отказ изделия (табл. 5.3).

Таблица 5.3. Прогнозные значения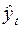

Уравнение регрессии
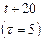
	256,5	288,5	320,5	352,5	384,5

Следует отметить, что суммарный «вес» последних значений временного ряда можно вычислить по формуле

.

Так, для двух последних наблюдений ряда () величина

.

Дата добавления: 2015-07-25