Критерии устойчивости

Критерий устойчивости – это математическая формулировка условий, которым удовлетворяют коэффициенты характеристического уравнения устойчивой системы.

В теории автоматического регулирования наибольшее распространение получили алгебраические критерии Рауса, Гурвица, Вышнеградского; частотные критерии Михайлова и Найквиста и критерии, основанные на использовании логарифмических частотных характеристик разомкнутой системы. С математической точки зрения все критерии устойчивости эквивалентны.

Рассмотрим подробнее названные критерии устойчивости.

Алгебраические критерии. Алгебраические критерии определяют совокупность алгебраических неравенств, описывающих связи между коэффициентами характеристического уравнения системы.

Критерий Рауса был предложен английским механиком Э. Раусом для отыскания условий, при которых все корни характеристического уравнения имеют отрицательные вещественные части, и применяется при определении устойчивости систем высокого порядка. Он удобен при использовании ЭВМ. Этот критерий формулируется в виде некоторого правила (алгоритма), путем составления так называемой таблицы Рауса исходя из коэффициентов характеристического уравнения замкнутой системы.

В первой строке записываются коэффициенты с четными индексами, начиная с коэффициента а ₀. Во второй строке записываются коэффициенты с нечетными индексами. Коэффициенты последующих строк вычисляются по приведенным в таблице формулам. Всего должно быть записано п + 1 строк.

Условие устойчивости Рауса формулируется следующим образом: замкнутая система устойчива, если все коэффициенты первого столбца таблицы имеют один и тот же знак, т. е. при а ₀ > 0 все коэффициенты первого столбца положительны. Это условие является необходимым и достаточным для суждения об устойчивости.

Если один из элементов первого столбца равен нулю, а остальные положительны, система находится на границе устойчивости – характеристическое уравнение имеет пару чисто мнимых корней.

Критерий Гурвица был сформулирован швейцарским математиком Гурвицем и сводится к нахождению детерминированных неравенств из характеристического уравнения. Чтобы в характеристическом уравнении при а ₀ ¹ 0 замкнутой системы все корни имели отрицательные вещественные части, необходимо и достаточно, чтобы удовлетворялись неравенства: при

а ₀ > 0; D₁ > 0; D₂ > 0; D₃ > 0; D₄ > 0; D _n > 0,

где

и т. д.

Следовательно, критерий Гурвица сводится к тому, что при а ₀ > 0 должны быть больше нуля все п определителей, получаемых из квадратной матрицы коэффициентов.

Квадратная матрица из коэффициентов характеристического уравнения для замкнутой системы составляется следующим образом. По диагонали от верхнего левого угла до правого нижнего выписываются все коэффициенты, начиная с коэффициента с индексом 1 до коэффициента с индексом п. От каждого коэффициента, стоящего по главной диагонали, по вертикали вверх записываются коэффициенты с возрастающими индексами, а вниз – с убывающими. Места в матрице коэффициентов с индексами больше п и меньше 0 заполняются нулями.

Частотные критерии. Частотные критерии позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии являются графоаналитическими и получили широкое применение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, обладают хорошей наглядностью.

Критерий Михайлова. Этот критерий устойчивости был предложен советским ученым А. В. Михайловым и позволяет судить об устойчивости замкнутой системы на основании рассмотрения некоторой кривой.

Кривая Михайлова представляет собой годограф вектора (характеристический полином) получаемый из характеристического уравнения системы путем подстановки р = jw.

D (jw) = a ₀(jw) ⁿ + a ₁(jw) ^{n– 1} + … + a_{n– 1}(jw) + a_n.

Выделив в правой части последнего уравнения вещественную U (w) и мнимую V (w) части, можно записать D (jw) = U (w) + jV (w).

Формулировка критерия Михайлова сводится к следующему: чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая Михайлова при изменении частоты w от 0 до ¥, начинаясь при w = 0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов, уходя в бесконечность в последнем квадранте, где п – порядок характеристического уравнения.

На рис. 1.24 показаны типичные кривые Михайлова для устойчивых систем 1–5 порядков с равным значением коэффициента а_п.

Рис. 1.24. Годограф Михайлова для устойчивых систем

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов плоскости [ U; jV ].

Критерий Найквиста. Этот частотный критерий был предложен американским ученым Найквистом для исследования устойчивости усилителей с обратной связью и дает возможность определить устойчивость замкнутой системы по АФЧХ W (jw)ее разомкнутой цепи, если удовлетворяется условие lim W (jw) = c (в частности, с = 0). Преимущество критерия Найквиста состоит в том, что амплитудно-фазовая характеристика разомкнутой системы может быть построена не только расчетным путем, но и экспериментально. Если имеется передаточная функция разомкнутой системы, то подставляя в ее выражение p = jw, получаем частотную передаточную функцию разомкнутой системы:

или

W (jw) = U (w) + jV (w) = А (w)е ^{j j(w)},

где 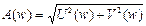– модуль частотной передаточной функции;

j(w) = arctg V (w) / U (w) – фаза частотной передаточной функции.

Обычно для W (jw) выделяют в числителе и знаменателе действительную и мнимую части и избавляются от мнимости в знаменателе путем умножения чиcлителя и знаменателя на комплексно сопряженный знаменатель, т. е. если:

то

Если изменять частоту w от –¥ до +¥, то вектор W (jw) будет меняться по величине и фазе, т. е., вычисляя амплитуду и фазу при каждом значении w, можно построить на комплексной плоскости амплитудную фазовую частотную характеристику разомкнутой системы (рис. 1.25).

Рис. 1.25. Годограф Найквиста для устойчивых систем

Если разомкнутая система устойчива, то критерий Найквиста формулируется: для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы W (jw) при изменении частоты w от 0 до ¥ не охватывала точку с координатами [–1; j 0].

Запас устойчивости системы. При оценке устойчивости систем необходимо определить величину запаса устойчивости, т. е. степень удаленности системы от границы устойчивости.

В случае применения критерия Гурвица запас устойчивости можно оценить по тому запасу, с которым выполняются входящие в этот критерий неравенства. При использовании критериев Михайлова и Найквиста запас устойчивости определяется удаленностью соответствующих характеристик от критического положения, при котором система находится на границе устойчивости. Для критерия Михайлова это будет удаленность годографа W (jw) от начала координат, а для критерия Найквиста – удаленность характеристики W (jw) от точки (–1; j 0).

Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины: запас устойчивости по фазе Dj и запас устойчивости по амплитуде D А.

Запас устойчивости по амплитуде определяется величиной допустимого увеличения АЧХ, при котором система окажется на границе устойчивости.

Запас устойчивости по фазе определяется величиной Dj, на которую должно возрасти запаздывание по фазе в системе на частоте среза w _с, чтобы система оказалась на границе устойчивости. Для определения Dj проводится дуга радиусом 1 до пересечения с АФЧХ. При проектировании САУ рекомендуется выбирать Dj ³ 30º и DA ³ 0,7.

Дата добавления: 2015-07-25