Математическое описание элементов и систем автоматики

Для анализа и расчета САР необходимо иметь математическое описание (математическую модель) объекта управления. Получение математического описания объекта управления, в определенном смысле математической модели по реализации его входных и выходных сигналов, называется его идентификацией.

Применение общих методов описания объектов в теории управления приводит в простейшем случае к представлению на нижнем уровне процесса в виде одномерного объекта (рис. 1.16), на входе которого действует переменная x (t), характеризующая какое-либо свойство сырья или параметр, а на выходе – переменная у (t), характеризующая какое-либо свойство объекта или выходной показатель процесса.

Рис.1.16. Блок-схема одномерного объекта управления

Проблема индентификации таких объектов в целях построения САУ заключается в определении статических и динамических характеристик в виде адекватных математических моделей в рабочем диапазоне.

Современные методы идентификации используют сочетание аналитического и экспериментальных методов. Это связано с тем, что чисто аналитический подход во многих случаях не обеспечивает получение математической модели, в достаточной степени соответствующей реальному объекту управления. Поэтому комбинированный подход, когда общий вид математического описания определяется аналитически, а значения коэффициентов, соответствующих конкретному объекту управления, – экспериментально, наиболее эффективен. Для сложных объектов задачи идентификации решаются с использованием ЭВМ, что значительно расширяет возможности аналитического и экспериментальных методов на стадии отработки и проверки соответствия математической модели.

Аналитический метод построения математического описания в статике и динамике не требует особых пояснений. Используя известные физические, химические, механические и другие закономерности, по которым осуществляются процессы, составляют уравнения, устанавливающие взаимосвязь выходных и входных переменных объекта в стационарных условиях (не зависящих от времени), и уравнения, устанавливающие зависимость изменения во времени выходной величины от заданного изменения входного воздействия.

Экспериментальные методы базируются на использовании специальных приемов активного и пассивного эксперимента, облегчающих получение необходимых зависимостей на реальном технологическом процессе в условиях производства. Активный эксперимент предусматривает нанесение скачкообразных изменений входной величины в пределах, допустимых технологическим регламентом. Наибольшее применение для исследования статических характеристик получили классический метод активного эксперимента и метод факторного планированного эксперимента. Для исследования динамических характеристик объекта управления применяют методы временного анализа.

Пассивные экспериментальные методы применяются при определении как статических, так и динамических характеристик на базе корреляционного и регрессионного анализа данных нормальной эксплуатации промышленного объекта.

Временной метод практически сводится к экспериментальному снятию переходной характеристики или кривой разгона по каналу управления. Для пояснения метода на рис. 1.17 приведена схема оснащения исследуемого объекта измерительными приборами, позволяющими измерять вносимые изменения входной и выходных величин. При проведении эксперимента особое внимание обращают на синхронизацию регистрации входной и выходной величин. В начале эксперимента объект приводят в установившееся состояние. После этого изменяют скачкообразно входную величину на D х = 10 / 15 % максимально допустимого значения входной величины. Эксперимент считается законченным, когда выходная величина достигнет нового установившегося значения для объектов с самовыравниванием либо когда устанавливается постоянная скорость изменения выходной величины в случае исследования объекта без самовыравнивания. Для каждой точки опыты повторяют не менее двух–четырех раз.

Рис. 1.17. Схема оснащения исследуемого объекта измерительными приборами (И₁, И₂, …, И _n – измерительные приборы, P – регистратор)

На рис. 1.18, а приведена кривая разгона, полученная экспериментально для объекта, обладающего самовыравниванием, и показана графически «методом касательной» возможность определения параметров t₀ и Т ₀.

Рис. 1.18. Определение по кривым разгона динамических параметров объекта:

а – статического; б – астатического

Коэффициент передачи получают из соотношения:

.

На рис. 1.18, б по кривой разгона для объекта без самовыравнивания показано графическое определение запаздывания t₀, а параметры k ₀ и Т находят из соотношений:

, Т ₀ = 1 / k ₀.

Рассмотрим аналитический метод математического описания элементов автоматики.

Состояние любого динамического звена может быть охарактеризовано совокупностью соответствующих физических величин (скоростей перемещений, напряжений, токов и т. д.). Поскольку размерности этих величин различны, то их представляют обобщенными координатами. Порядок составления дифференциальных уравнений состоит в следующем:

1) определяются входная и выходная величины и действующие на них факторы;

2) выбирается начало отсчета;

3) выявляется и используется основной физический закон, определяющий связь между входной и выходной величинами. В механике, например, это законы Ньютона, в электротехнике – Кирхгофа и т. п.

Математическое описание физического закона связи входной и выходной величин в динамическом состоянии и является исходным дифференциальным уравнением. Рассмотрим порядок составления уравнений на примере.

Пример. Найти дифференциальное уравнение для гидравлического демпфера (рис. 1.19), если пренебречь влиянием массы m подвижных частей и принять за входную величину силу F, а за выходную – перемещение поршня у, т. е. y = f (F). Очевидно, что для нахождения этой зависимости следует использовать третий закон Ньютона и записать, что F = åР = Р_д + P_тр + P_и + P_в.

Рис. 1.19. Гидравлический демпфер

Силами инерции Р _и, трения P _тр и сопротивления от веса P _в подвижных частей пренебрегаем ввиду их малости. Тогда действующая сила F будет равна только силе гидравлического сопротивления Р_д, т. е.

где с – коэффициент демпфирования.

С учетом массы подвижных частей, т. е. силы инерции уравнение движения поршня будет иметь вид:

.

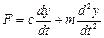После записи дифференциального уравнения вводят те или другие упрощения. Прежде всего исключаются факторы, мало влияющие на энергетические и другие свойства динамического звена, а также параметры, значения которых поддерживаются постоянным естественным путем или за счет работы других звеньев системы. Тогда обобщенное уравнение звена можно представить в таком виде:

,

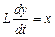где L – величина (оператор), характеризующая собственные свойства звена.

В общем виде дифференциальные уравнения можно представить как

F (y ', y, х; f)= 0 – уравнение 1-го порядка,

или

F (y ", y ', y ', f) = 0 – уравнение 2-го порядка и т. д.

Полученные уравнения чаще всего оказываются нелинейными, решить которые аналитическим путем бывает затруднительно, а иногда и невозможно. Поэтому на практике нелинейные уравнения приводят к виду линейных. При этом надо помнить, что линеаризации подвергаются только неразрывные функции (релейные и импульсные функции линеаризовать нельзя). В основе линеаризации нелинейных уравнений лежит предположение, что в исследуемом динамическом процессе переменные изменяются так, что их отклонения (D х; D y) от установившегося значения (х ⁰; у ⁰) остаются все время достаточно малыми. Для следящих систем и большинства систем управления по отклонению это условие выполняется.

Дата добавления: 2015-07-25