При исследовании элементов и систем

Поведение любого звена и системы управления как в статике, так и в динамике зависит от изменения во времени внешних воздействий, законы изменения которых, как правило, заранее неизвестны. Поэтому при исследовании элементов и систем используют так называемые типовые законы изменения внешних воздействий.

Единичная ступенчатая функция. В качестве типовых внешних воздействий принимают так называемые полиноминальные воздействия:

задающие , (3.1)

возмущающие , (3.2)

где n = 0, 1, 2, … – натуральное число;

g_n, f_n – постоянные задающая и возмущающая величины.

При п = 0 выражения 3.1 и 3.2 определяют ступенчатые типовые воздействия:

g (t) = g ₀ 1(t),

f (t) = f ₀ 1(t).

Воздействию (например, возмущающему) f (t) = f ₀ 1(t) соответствует скачкообразное увеличение или уменьшение нагрузки в САУ скорости вращения вала двигателя, мгновенное подключение или отключение группы потребителей энергии в САУ напряжения генератора и т. д.

В выражениях 3.1 и 3.2 функция 1(t) есть единичная ступенчатая функция:

0 при t< 0

1(t) = (3.3)

1 при t> 0

Эта функция может быть в виде единичного мгновенного скачка (рис. 1.13, а) и единичного мгновенного импульса.

Воздействию g (t) = 1(t) соответствует, например, процесс перенастройки системы стабилизации на новое значение регулируемой величины.

Рис. 1.13. Типовые законы изменения внешних воздействий

Единичный мгновенный импульс бывает 1-го (рис. 1.13, б) и 2-го (рис. 1.13, в) рода, т. е. это скачкообразные функции с длительностью скачка t, стремящемся к нулю, или первая и, соответственно, вторая производные от единичного скачка.

Аналитически импульсы представляются в виде g (t) = 1¢(t) – первого рода и g (t) = 1"(t) – второго рода.

При n = 1 типовые воздействия изменяются с постоянной скоростью, т. е.:

g(t) = g ₁ t 1(t);

f (t) = f ₁ t 1(t),

где g ₁ и f ₁ – постоянные значения. Графическое представление этих функций показано на рис. 1.13, г.

При n = 2 типовые воздействия изменяются с постоянным ускорением. Их аналитическое и графическое изображение представлено на рис. 1.13, д.

;

.

Единичная дельта-функция используется также в качестве типового внешнего воздействия (рис. 1.13, е). Аналитическое выражение этой функции:

0 при t ¹ 0

d(t) =

¥ при t = 0

Воздействие с помощью дельта-функции представляется как:

g (t) = g ₀d(t);

f (t) = f ₀d(t).

Дельта-функция обладает тем свойством, что:

,

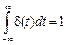т. е. дельта-функция представляет математическую идеализацию импульса бесконечно малой длительности, имеющего конечную площадь, равную единице, и относится к числу функций специального класса, называемых обобщенными.

Воздействия с дельта-функцией хорошо отвечают работе САУ, функционирующих в условиях импульсных возмущений.

Гармонические воздействия. Кроме полиноминальных воздействий весьма часто, особенно при частотных методах анализа и синтеза систем, применяются гармонические воздействия (рис. 1.13, ж):

g (t) = A sin w _g t;

f (t) = А sin w_f t,

где А – амплитуда гармонического сигнала,

w _g, w_f – круговые частоты гармонических сигналов.

Эти воздействия хорошо отвечают реальным условиям работы систем в условиях качки, сильных вибраций и т. п.

Дата добавления: 2015-07-25