Автоматического управления

Устойчивость является необходимым условием работоспособности, т. е. система должна нормально функционировать и быть нечувствительной к различного рода внешним возмущениям.

Под устойчивостью САУ понимается способность системы поддерживать заданное значение регулируемого параметра с определенной точностью и восстанавливать его после окончания переходного процесса.

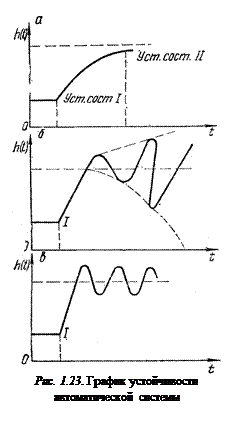
Следовательно, по характеру переходного процесса можно судить об устойчивости системы (рис. 1.23). Если система устойчива (рис. 1.23, а), то переходная характеристика lim h (t) = 0. Если система неустойчива, т. е. когда lim h (t) = ¥, то она не возвращается в состояние равновесия, из которого была выведена и может удаляться от состояния равновесия, либо совершать недопустимо большие колебания (рис. 1.23, б). При этом известно, что при небольших возмущениях система устойчива, а при больших воздействиях может оказаться неустойчивой.

Поэтому в общем случае, рассматривая нелинейные системы, вводится понятие устойчивости в «малом», в «большом» и в «целом».

Система устойчива в «малом», если известна область устойчивости, но неизвестны границы этой области, в «боль-шом», когда определены границы области устойчивости и в «целом», когда она возвращается в исходное состояние при любых начальных отклонениях, возмущениях. Устойчивость «в целом» для определенного класса нелинейности называют «абсолютной» устойчивостью.

Исследование устойчивости САР целесообразно проводить в аналитическом виде, т. е. путем нахождения корней характеристического уравнения. Не приводя необходимых доказательств на основании теорем А. М. Ляпунова, следует отметить, что если все корни характеристического уравнения располагаются в левой полуплоскости комплексной плоскости (левее мнимой оси), то линейная система автоматического управления является устойчивой.

Очевидно, что мнимая ось является границей устойчивости. Система будет находиться на границе устойчивости при наличии нулевого корня, пары мнимых корней или бесконечно удаленного корня (p_i = ¥).

Если в характеристическом уравнении свободный член равен нулю (а_n = 0), то это говорит о наличии нулевого корня и такая система называется нейтрально уcтойчивой (рис. 1.23, в), так как она устойчива не относительно управляемой величины у, а скорости ее изменения dy / dt.

Очевидно, для определения устойчивости необязательно знать значение корней характеристического уравнения, достаточно убедиться в отрицательности вещественных частей корня. Методы, основанные на установлении факта их отрицательности, называются критериями устойчивости.

Дата добавления: 2015-07-25