Передаточные функции автоматических систем

Системы автоматического управления и многие сложные элементы состоят из некоторого числа соединенных между собой динамических звеньев. Наиболее простыми и часто встречающимися (типовыми) соединениями звеньев являются (при этом имеется в виду разомкнутая цепь звеньев): последовательное, параллельное, встречно-параллельное или соединение с обратной связью.

При последовательном соединении выходная величина каждого из звеньев, кроме последнего, служит входной величиной последующего звена (рис. 1.20, а).

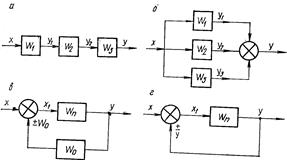
Рис. 1.20. Передаточные функции автоматических систем

Эквивалентная передаточная функция такого соединения или передаточная функция разомкнутой системы определяется как:

где у ₁, у ₂, у ₃ – изображения по Лапласу переменных.

При параллельном соединении (рис. 1.20, б) все звенья имеют одну и ту же входную величину, а их выходные величины суммируются. Тогда для такого соединения можно записать выражение для эквивалентной передаточной функции:

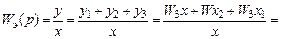
Для встречно-параллельного соединения (рис. 1.20, в), состоящего из звена в прямой цепи с передаточной функцией W _п и звена в обратной цепи с передаточной функцией W ₀, можно составить следующие равенства:

Решив эти уравнения относительно

получим эквивалентную функцию

,

где знак «+» в знаменателе соответствует отрицательной обратной связи, а знак «–» – положительной.

В случае, если передаточная функция обратной связи W ₀(p) = 1 (жесткая единичная обратная связь), структурная схема имеет вид как на рис. 1.20, г.

В общем случае передаточная функция разомкнутой системы представляет собой рациональную дробь.

Целесообразно, как и для отдельного звена, передаточную функцию всей системы W (p)приводить к стандартному виду:

,

где Q (p) и V (р) – многочлены с единичными коэффициентам при младших членах.

В расчетах замкнутых автоматических систем применяют три основных вида передаточных функций:

1. Главная или основная передаточная функция Wg (р) по задающему воздействию. При этом принимается условно f (t) = 0.

Например, имеется схема замкнутой одноконтурной САУ (рис. 1.21).

Рис. 1.21. Схема замкнутой одноконтурной САУ

Запишем уравнения для прохождения сигнала g (t):

х = g – y; y ₁ = W ₁ x; у ₂ = W ₂ y ₁= W_k;

или

y ₂ = W ₁ W ₂ x = W ₁ W ₂(g – y).

откуда

где W ₁ W ₂ = W(p) – передаточная функция разомкнутой системы.

Следовательно, в общем виде можно записать:

2. Передаточная функция по возмущающему воздействию W_f (р). В этом случае условно принимается g (t) = 0. Для рис. 1.21 запишем:

y = y ₂ + y ₃ = xW ₁ W ₂ + fW_k = – yW ₁ ∙ W ₂ + fW_k,

откуда

При этом передаточная функция W _k зависит от места приложения возмущающего воздействия.

3. Передаточная функция для ошибки. По задающему воздействию условно принимаем f(t) = 0

W _eg(p) = x (p) / g (p) = X/G.

Передаточная функция для ошибки по возмущающему воздействию (g (t) = 0):

,

определяется из системы уравнений:

х = – у = –(у ₂ + y ₃) = –(xW ₁ W ₂ + fW_k);

x (1 +W ₁ W ₂) = –fW_k,

откуда

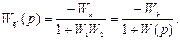
Важно отметить, что знаменатель всех видов передаточной функции замкнутой системы один и тот же.

Вычислению передаточных функций для многоконтурных систем должно предшествовать свертывание схемы к одноконтурной одномерной.

Для замкнутой системы в целом имеем:

Имея передаточные функции можно алгебраически записать ее дифференциальные уравнения. В этом состоит, в частности, одно из важных практических преимуществ использования аппарата передаточных фнкций.

Дата добавления: 2015-07-25